��H�ɕ����̒�R���o�Ă���ꍇ�A�u����v�u����v�i����т��̑g�ݍ��킹�j������B
�u����v�͂��̂܂ܑ����݂̂ł��邽�ߐ����s�v�B�u����v�������B
��R��3�̕���ڑ��̏ꍇ���Ƃ���B
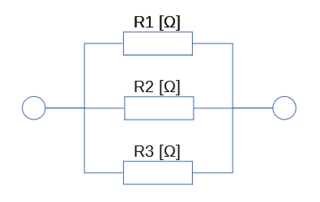
��RR1�AR2�AR3�Ƃ��̍�����RR0�Ƃ���ƁA�v�Z���͈ȉ��ƂȂ�B
1/R0 ���@1/R1�@�{�@1/R2�@+1/R3
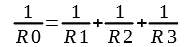
����̏ꍇ�A�t�����o�Ă���B����͒�R�𑫂��݂̂ł��邪�A����́A�d���̒ʂ蓹�������Ă��邽�߁A�d���̒ʂ�₷�����l�����邽�߁A��R�̋t����p���Ă���B
R0���t���ł��邽�߁A���߂₷���悤�ɕό`����Ɖ��L�ƂȂ�B
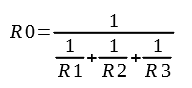
�ł́A���ۂɋ��߂Ă݂�B
R1=2���AR2=3���AR3=5���Ƃ���B
������A��L�̎��ɓ��Ă͂߂�ƁA�ȉ��̂悤�ɎZ�o�ł���B
1 ÷ ( 1/2 + 1/3 + 1/5 ) = �@0.9677
�ʏ�̓d��ƁA���d��Ƃő��삵�Ă݂�B
���ʏ�̓d��
�ʏ�̓d��ł́A�u�������[�@�\�v���g�p����B
[�P][÷][�Q][M+]
[�P][÷][�R][M+]
[�P][÷][�T][M+]
[�P][÷][RM�i�������Ăяo���j][M+]
�i�K�v�ł���A�ŏ���[CM�i�������N���A�j]�j
�����d��
���d��̏ꍇ�A�������̓��͕��@������B
�i�����ł̓V���[�v��EL-509T���g�p���Ă��邪�A���А��ł��قړ��l�j
�@�ʏ�̓d��Ɠ������A�������[�@�\���g�p����B
�A�m÷�n�ł͂Ȃ��A�������g�p����
�@�@�L�[�́A
[�P][a/b][�Q][��]�����ڂ͎��ʂ�ł��邪�A�������͌�̃J�[�\���L�[��ς킵��
�B�m÷�n�ł͂Ȃ��A�t�����g�p����A
�@�@�L�[�́A
[�Q][2ndF][x-1]
�C1/R0�̉ӏ����A�ŏ�����u1÷�i1/R1+1/R2+1/R3�j�v�Ƃ����������čs�����A�u1/R1+1/R2+1/R3�v�����߂Ă���t���Ƃ���B
�Ȃ��A�����̏����̕\���ύX�́mCHANGE�n�L�[�ōs���A
�E�ŏ�����u1÷�i1/R1+1/R2+1/R3�j�v
�E�u1/R1+1/R2+1/R3�v�����߂Ă���t��
�ȏ�
�^�O�F���d��@�g����
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
-
no image
-
no image
-
no image
-
no image
-
no image