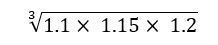プログラマーであれば、べき乗の計算はjavaだとmath.powメソッドを使用する。powはpowerの略であるので、ここでは「べき」を使用した。
日常でべき乗を行うことはあるだろうか、そしてその逆のべき乗根を必要とすることはあるだろうか。
使用する局面は、伸び率の計算や金利(複利)の計算が有名である。
そこで、伸び率、金利の計算を行う。
(関数電卓はシャープのEL-509Tを使用しているが、他社製でも特に大きな違いはない)
べき乗
300円は、金利4%で、5年後にはいくらになるか?
金額:300円
期間:5年
金利(年利):4%
5年分かけた場合
300 × 1.04 × 1.04 × 1.04 × 1.04 × 1.04 = 364
(ちなみに、4%は、1.04倍となる)
ちなみに、(小数切り捨て)だ。
この5年分をn乗とした場合
300 × 1.04 ^ 5 = 364
これを、関数電卓で作業する。
べき乗のキーは「yx」であり、yのx乗である。
[3][0][0][×][1][.][0][4][yx][5]
「yx」を押してから、「y」「x」を入力する。
キーを押す順が、「y」を押してから「yx」の場合、カーソルで入力位置を移動させることになる。
べき乗根
最初と最後の状態から、年利を出してみる。
つまり、5年間分から年平均を求める。1.04が結果として得られるはずである。
なお、5年間の伸び率の算出は、最後÷最初であり、
364 ÷ 300 = 1.217
である。
方法は「n乗根」と「1/n乗」の2通りある。
例えば、81の2乗根(平方根)は、ルート81(√81)=9であり、
他方では、81の1/2乗(81^(1/2))と同じ結果となる。
(1)n乗根
5 √ 1.217
[5][2ndF][x√][1][.][2][1][7]
結果で1.04を得ることができた。
(2)1/n乗
1.217 ^ (1/2)
[1][.][2][1][7][yx][1][÷][5]
結果は先のと一致する。
以上
タグ:関数電卓 使い方
【このカテゴリーの最新記事】
-
no image
-
no image
-
no image
-
no image
-
no image
-
no image