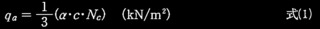2024年07月17日
令和元年度修了考査 構造設計(記述式)問題2
問題2
図1(a)及び図1(b)に示すような長期鉛直荷重を受ける門型骨組の柱の座屈に関する次の設問について解答せよ。各部材の材料特性・断面性能は、表1のとおりである。なお、長期許容圧縮応力度 fcは式(1)を用い、有効座屈長さの評価に関しては、図2に示す算定図表から得られる座屈長さ係数 K を用いるものとする。各部材は十分に横補剛されており、構面外座屈はしないものとする。
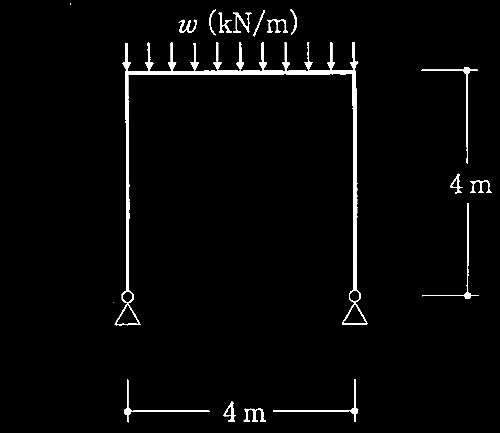
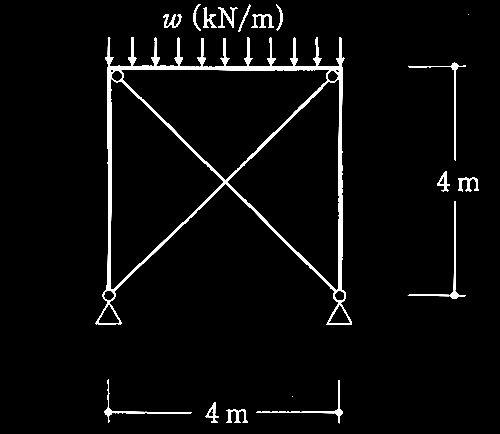
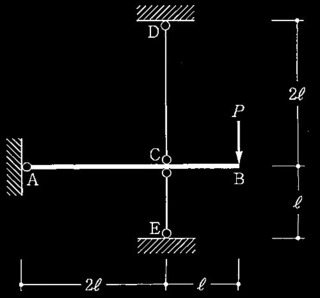
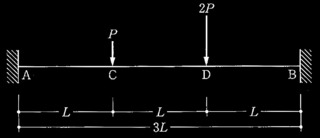
(a)門型骨組 (b)ブレース付き門型骨組
図1
表1 各部材の材料特性 断面性能
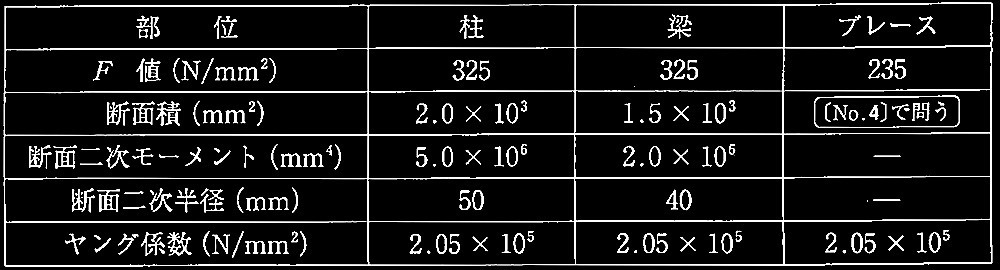
圧縮材の座屈の長期許容応力度 fc

(平成13年国土交通省告示第1024号第1第三号口表1より)
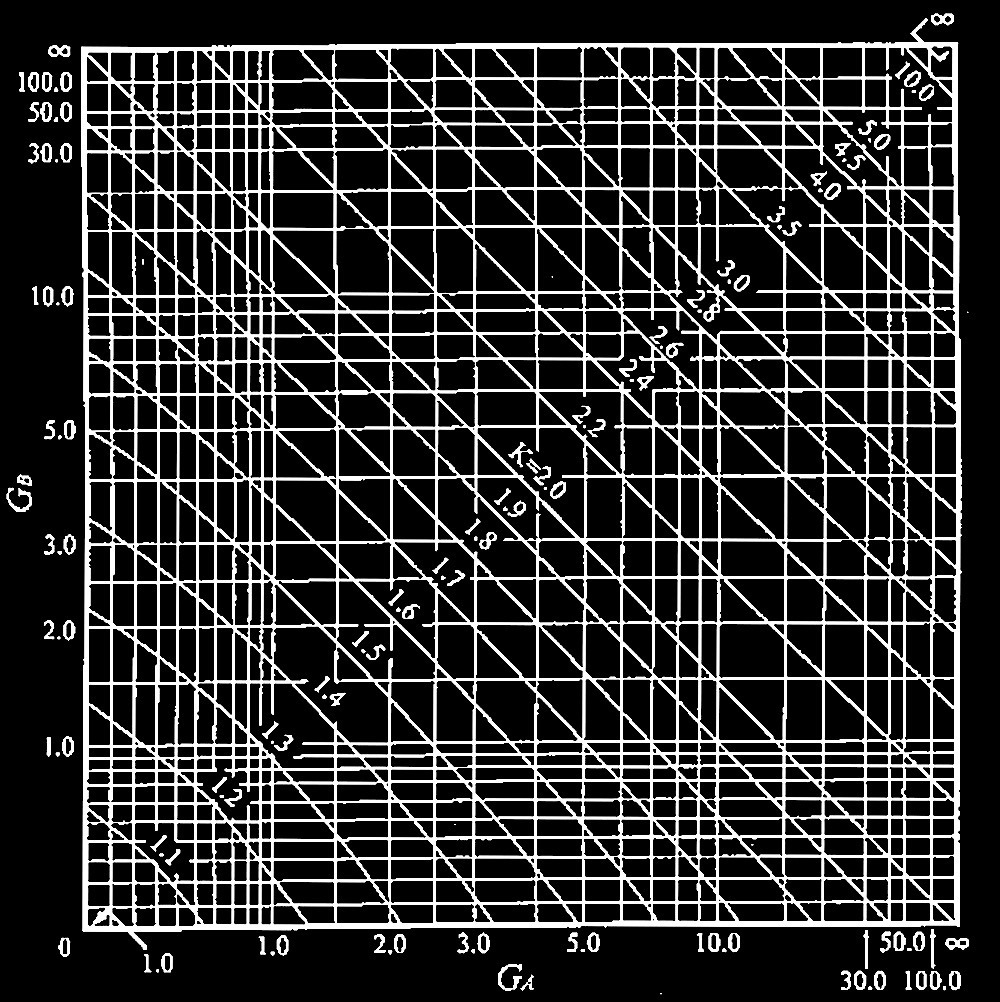
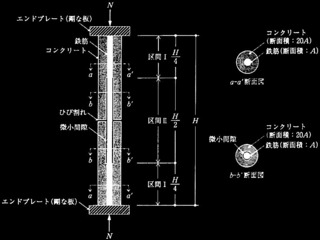
(a) 水平移動が拘束されない場合のK
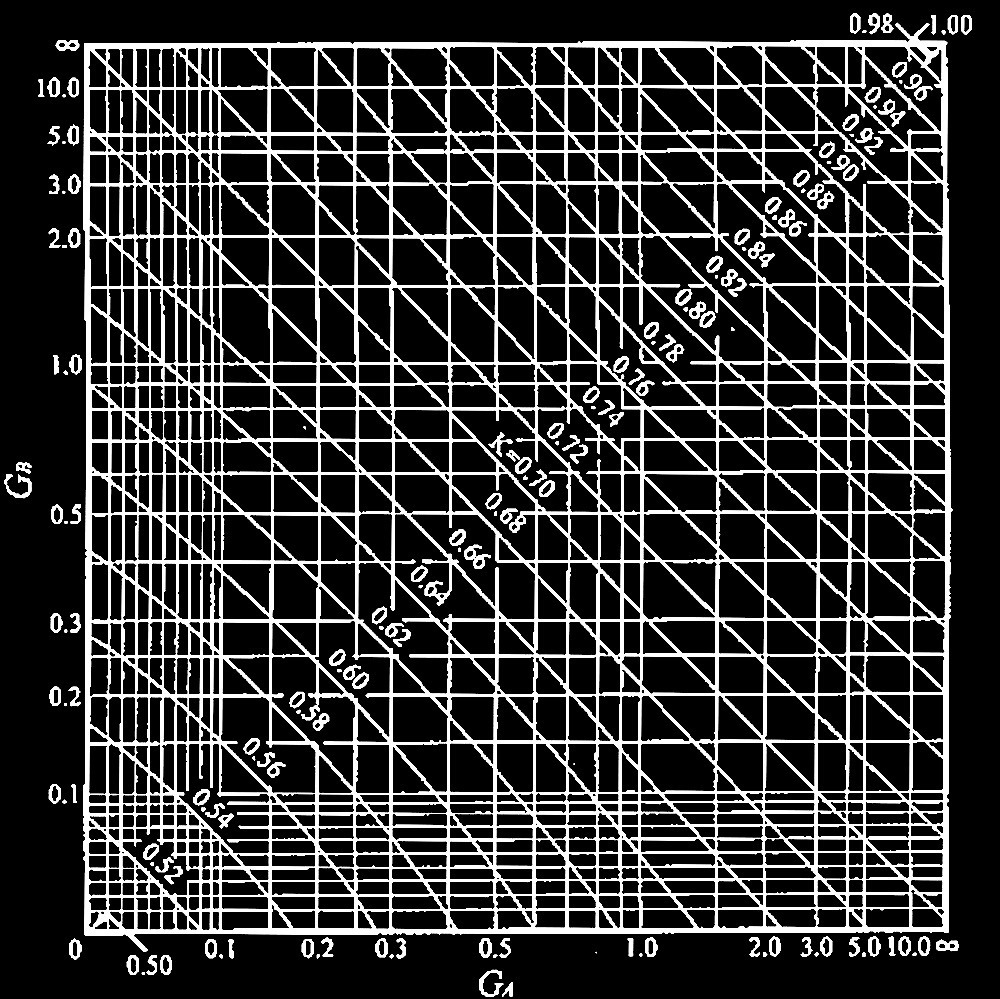
(b) 水平移動が拘束される場合のK
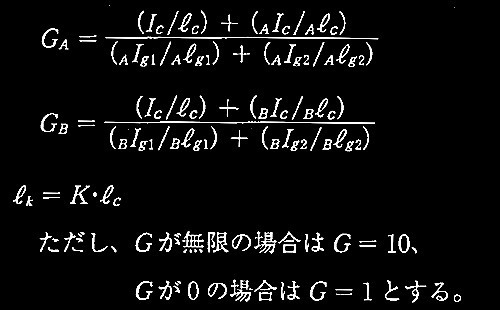
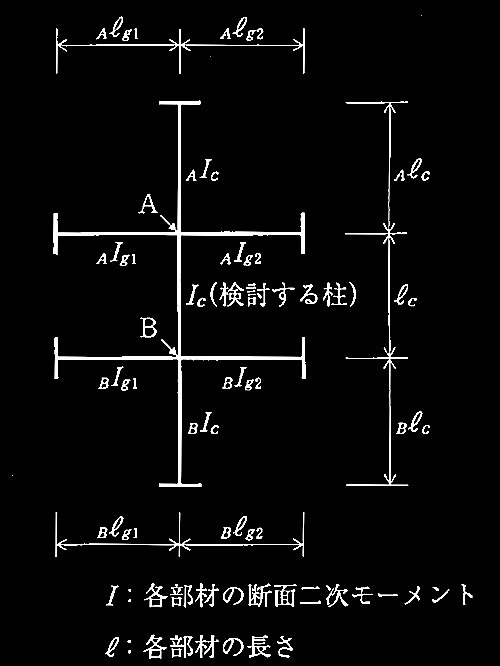
図2 柱の座屈長さ係数Kの算定図表
(引用:日本建築学会「鋼構造座屈設計指針」(一部編集))
図1の門型骨組の左側の柱の場合、接続する部材は柱頭の右側の梁のみであり、
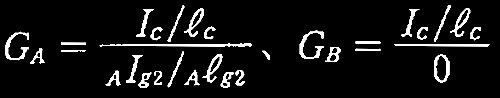
となる。
[ No.1 ]
図1の門型骨組の柱の座屈長さ係数 K を求めるためのGA及びGBの値を求めよ。
答え
[ 解答 ]
柱の座屈長さ係数Kの算定図表を門型骨組の柱にあてはめると以下の通りである。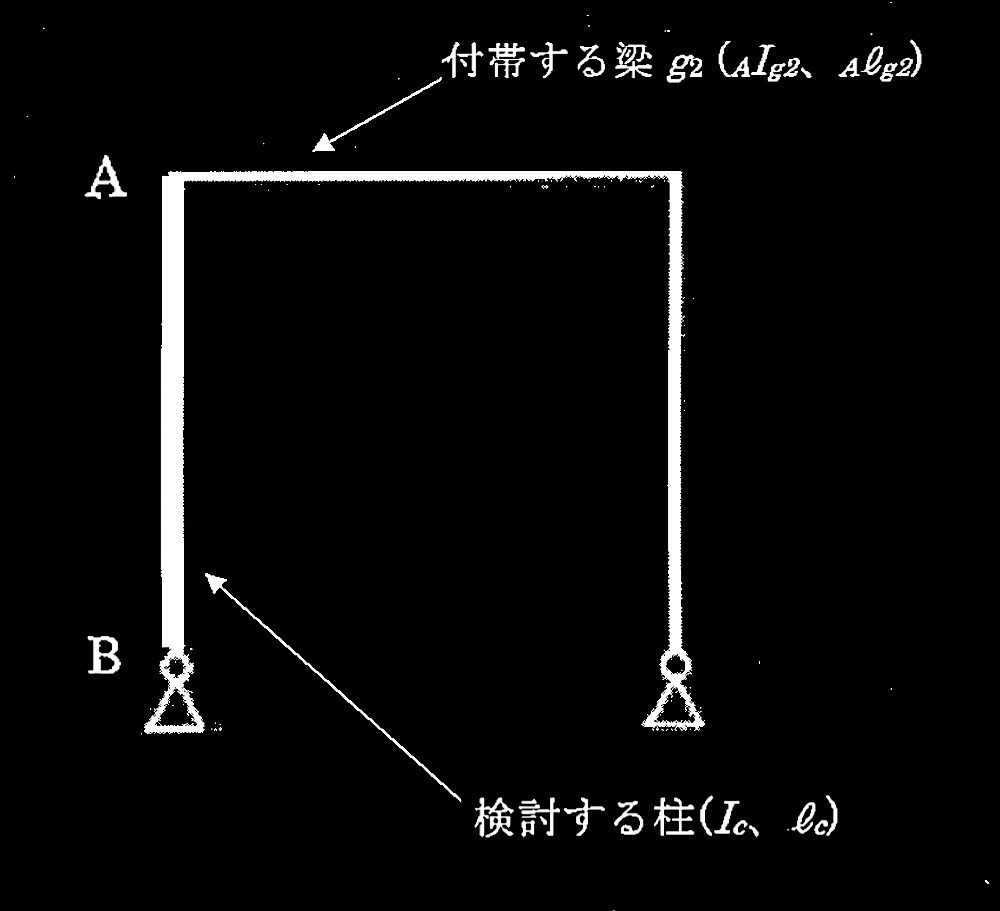
GA= (Ic/ℓc) / (AIg2/ Aℓg2)
= (5.0 × 106 / 4.0 × 103) / (2.0 × 106 / 4.0 × 103)
= 2.5
GB= lc / ℓc / 0 = ∞
→ 無限の場合はG= 10とすることから、10.0
[ No.2 ]
図1 (a)の骨組について、次の①~③の値を求めよ。
① 柱の有効座屈長さ(単位:mm)
② 柱の長期許容圧縮応力度(単位:N/mm2)
③ 柱が長期許容圧縮応力度に達するときの柱軸力(単位:kN)
答え
[ 解答 ]
①柱の有効座屈長さは、水平移動が拘束されない場合のKの表でGA= 2.5、 GB= 10.0となる点のKは2.2であることから以下の数値となる。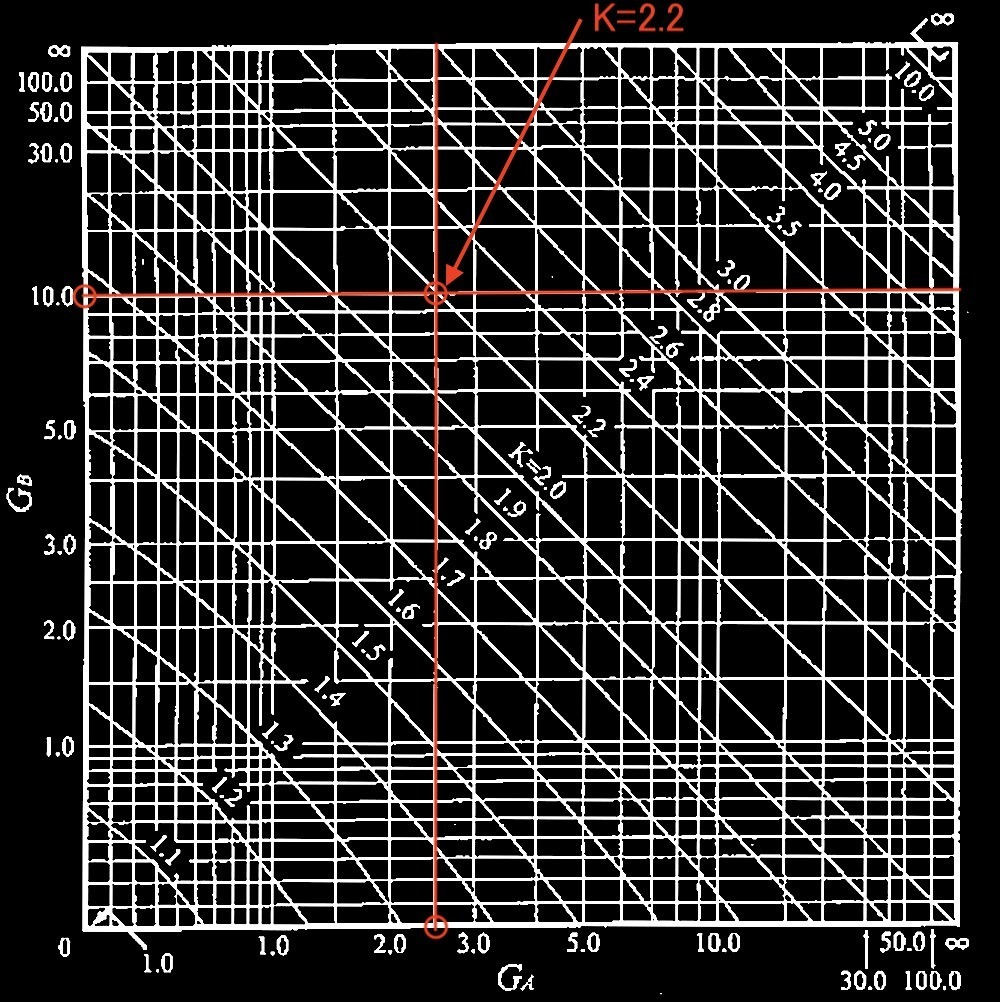
ℓk = K・ℓc = 2.2 × 4,000 = 8,800 mm
②柱の長期許容応力度は以下の式より求める。
ここで、限界細長比 Λ は
Λ = 1500/√(325/1.5) = 102
細長比λは
λ=ℓk / ic = 8800 / 50 = 176
よってλ> Λとなることから
fc = (18 / 65) / (176 / 102)2 × 325 = 30.2 N/mm2
※なお、数字の有効桁数は3桁とした。
③柱が長期許容圧縮応力度に達するときの軸力をN1とすると
N1= fc × A = 30.2 × 2.0 × 103/1000 = 60.4 kN
[ No.3 ]
柱頭の水平移動を拘束するために引張ブレースを入れた図1(b)の骨組について、次の①~③の値を求めよ。
①柱の有効座屈長さ(単位:mm)
②柱の長期許容圧縮応力度(単位:N/mm2)
③柱が長期許容圧縮応力度に達するときの柱軸力(単位:kN)
答え
[ 解答 ]
①柱の有効座屈長さは、水平移動が拘束される場合のKの表で
GA= 2.5、 GB=10.0
となる点のKは0.92であることから
以下の数値となる。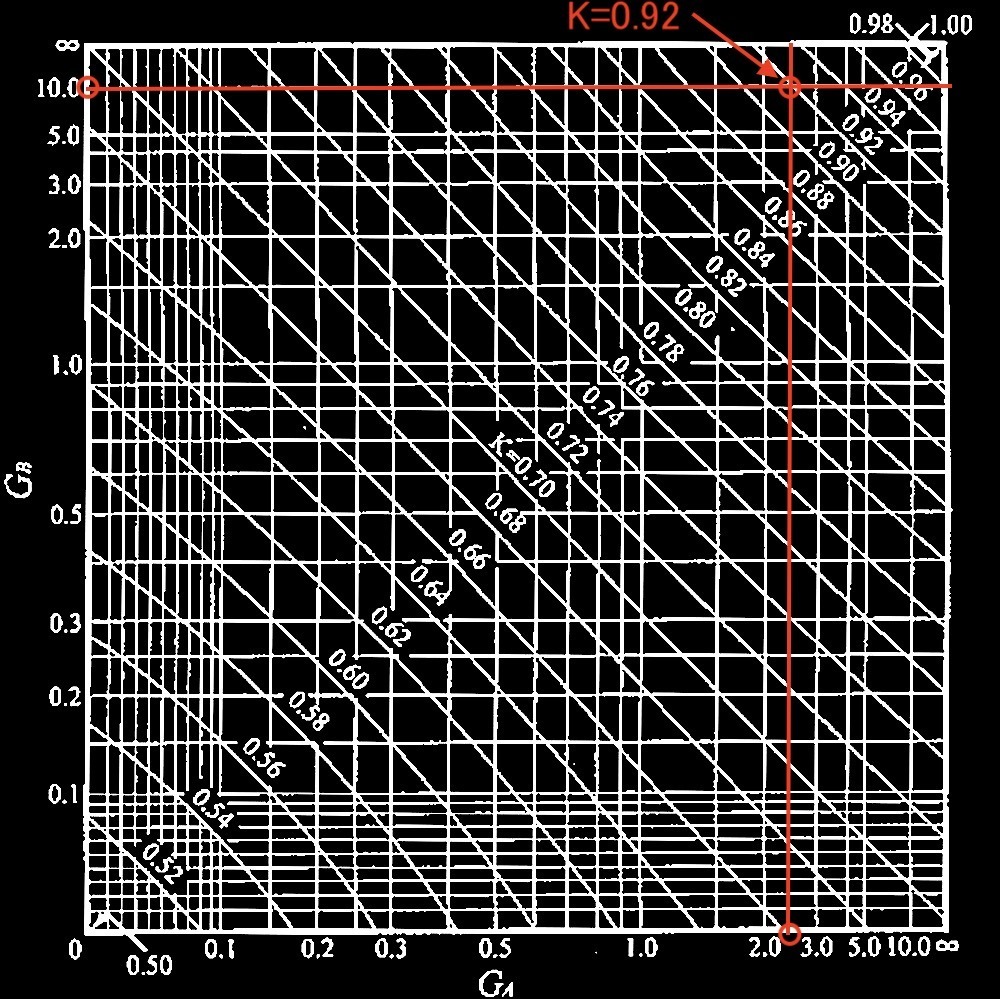
(b)水平移動が拘束される場合のK
ℓk = K・ℓc= 0.92 × 4,000 = 3,680mm
②柱の長期許容応力度は以下の式より求める。
ここで、限界細長比 Λ は
A = 1500 /√ (325/1.5) = 102
細長比λは
λ=ℓk/ ic = 3680 / 50 = 73.6
よって、λ< Λであることから
fc = 325・( 1 - 2/5×(73.6 /102)2) / (3/2 + 2/3 ×(73.6 / 102)2) = 139 N/mm2
③柱が長期許容圧縮応力度に達するときの軸力をN2とすると
N2 = fc × A = 139 × 2.0 × 103 / 1000 = 278 kN
[ No.4 ]
図1 (b)の骨組において、柱頭の水平移動を拘束するために必要なブレースの断面積を求めよ。なお、柱頭の水平移動を拘束するために必要な横力は、座屈耐力(柱が長期許容圧縮応力度に達するときの柱軸力)の2%でよいものとし、引張ブレースのみで負担するものとする。また、ブレースの材料は表1に示す鋼材とする。
答え
[ 解答 ]
水平移動を拘束するために必要な軸力をN3とし、[ No.3 ]から座屈耐力N2 = 278 kN
より、
N3 = 0.02 N2 = 0.02 × 278 = 5.56 kN
ここで、この軸カN3を横力Hとして、その横力は引張ブレースのみで負担すると仮定すると、引張ブレースに生じる軸力NBは、長期の問題では両側の柱に軸力が生じるため、以下のようにあらわせる。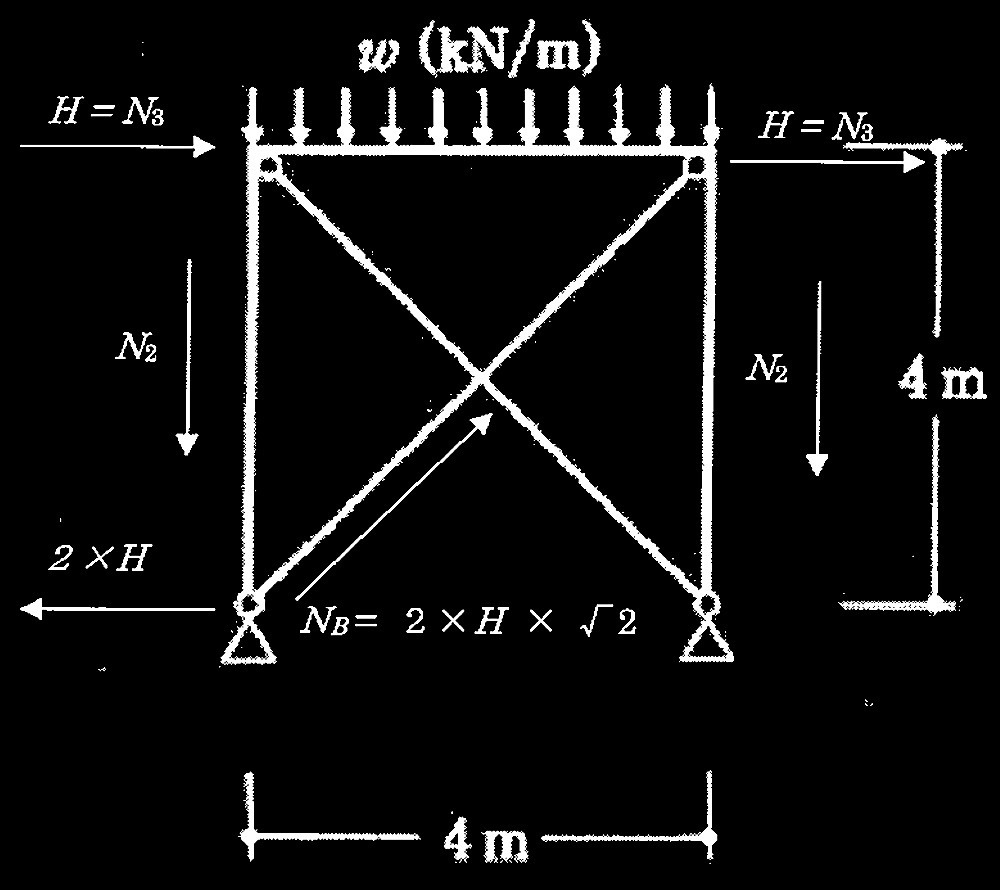
(b) ブレース付き門型骨組
NB = 2 × √ 2 N3 = 2 × √ 2 × 5.56 = 15.7 kN
よって、引張ブレースの必要断面積 ABは
長期許容引張応力度 ft = 235 / 1.5 = 157 N/mm2
であることから
AB= NB/ft = 15.7 × 1000/157 = 100 mm2
この記事へのトラックバックURL
https://fanblogs.jp/tb/12630093
※ブログオーナーが承認したトラックバックのみ表示されます。