2024年07月18日
令和元年度修了考査 構造設計(記述式)問題1
問題1
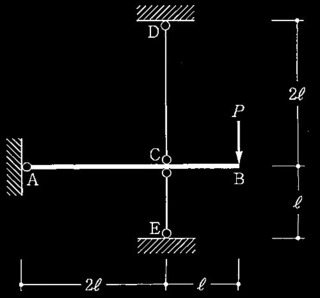
図1に示すように2点に大きさの異なる集中荷重を受ける両端固定梁の、崩壊荷重に関する次の設問について解答せよ。

図1 2点集中荷重を受ける両端固定梁
[ No.1 ]
構造物の崩壊荷重に関する次の枠内の文章の空欄 [ ① ]~ [ ③ ]に入るべき語句を記入せよ。
答え
[ 解答 ]
① 解の唯一性
② 上界
③ 下界
[ No.2 ]
塑性ヒンジの発生位置を考慮した崩壊メカニズムから、梁の真の崩壊荷重を求めた次の記述の空欄 [ ① ]~ [ ⑧ ]に入るべき数式又は数値を記入せよ。
設問[ No.1 ]で述べた3つの定理のうち、釣合条件と機構条件に立脚した定理を用いて梁の崩壊荷重 Puを求める。梁の3箇所に塑性ヒンジが発生すると崩壊メカニズムが形成され、図2 (a)~(d)に示す4つの崩壊メカニズムが考えられる。各塑性ヒンジは、崩壊メカニズムに達するまで十分な塑性回転能力を有しているものとし、全塑性モーメントはMpとする。

(a) 崩壊メカニズムー1

(b) 崩壊メカニズムー2

(c) 崩壊メカニズムー3

(d) 崩壊メカニズムー4
図2 梁の崩壊メカニズム
それぞれの崩壊メカニズムについて、仮想仕事法により崩壊荷重を求める。
(a) 崩壊メカニズムー1のとき
外力のなす仕事:P1・Lθ
内力のなす仕事:Mp・θ(A点)+Mp・2θ(C点)+Mp・θ(D点)
= 4Mp・θ
これらの仕事を等置して、P1・Lθ= 4Mp・θより、P1= 4(Mp/L)
(b) 崩壊メカニズムー2のとき
外力のなす仕事:P2・2Lθ+ 2P2・Lθ= 4P2・Lθ
内力のなす仕事:Mp・2θ(A点)+Mp・3θ(C点)+Mp・θ(B点)= 6Mp・θ
4P2・Lθ = 6Mp・θより、P2= 1.5(Mp/L)
(c) 崩壊メカニズムー3のとき
外力のなす仕事: [ ① ]
内力のなす仕事: [ ② ]
[ ① ]= [ ② ]より、P3 = [ ③ ]
(d) 崩壊メカニズムー4のとき
外力のなす仕事: [ ④ ]
内力のなす仕事: [ ⑤ ]
[ ④ ]= [ ⑤ ]より、P4= [ ⑥ ]
よって、この梁の真の崩壊メカニズムは、崩壊メカニズムー [ ⑦ ]である。
ここで、Mp= 470kN・m、L=2mとすると、真の崩壊荷重Puは [ ⑧ ]kNとなる。
答え
[ 解答 ]
① P3・Lθ十2P3 ・Lθ= 5P3・Lθ
②Mp・θ(A点)+Mp・3θ(D点)+Mp・2θ(B点)= 6Mp・θ
③上記より5P3・Lθ = 6Mp・θなので、これをP3について解くと
P3=1.2(Mp/L)
④ P4・0 + 2P4・ Lθ = 2L4・Lθ
⑤ Mp・θ(C点)+ Mp・2θ(D点)+Mp・θ(B点)= 4Mp・θ
⑥ 上記より 2P4・Lθ= 4Mp・θなので、これをP4ついて解くと
P4= 2.0(Mp/L)
⑦ 崩壊メカニズム1~4のうち崩壊荷重Pが最小になるものが真の崩壊メカニズムとなる。
∴ 3
⑧ 崩壊メカニズムー3の崩壊荷重P3=Puより
Pu= 1.2 Mp/L= 1.2・470 /2.0 = 282 kN
[ No.3 ]
設問[ No.2 ]で決定した真の崩壊メカニズム時の曲げモーメント図を、真の崩壊荷重Puの値を用いて答案用紙に描き、梁のどの位置においても、曲げモーメントが全塑性モーメントMp(= 470kN・m)を超えておらず、降伏条件を満たしていることを確かめよ。
答え
[ 解答 ]
崩壊メカニズムー3を真の崩壊メカニズム時と仮定すると、A点、D点、B点の曲げモーメントは Mp=470 kNmであり、残りC点の曲げモーメントの値を求めれば曲げモーメント図として図化できる。
ここで、梁B-Dは両端がMpに達しているため、梁のせん断力QB-Dは
QB-D = 470 kNm × 2 / 2.0 m = 470 kN
となる。
梁のせん断力QB-Dと右端の支点反力は釣り合うので、それをRBとすると
RB= QB-D = 470kN
が成り立つ。
ここで左右の支点反力は外力と釣り合うことから、左端の支点反力RAが求まる。
P1 + P2 = RA + RB
282kN + 564kN = RA + 470 kN
RA = 282 kN + 564 kN - 470 kN = 376kN
支点反力RAは梁A-Dの梁のせん断力QA-Dと釣り合うことから、以下の式が成り立つ。
RA=QA-D = 376kN
ここで、梁A-Dのせん断力QA-Dは左右端部の曲げモーメントの和を長さで除したものとなるため、
QA-D = (MA+ Mc) /L
376 = (470 +Mc)/ 2.0
Mc = 282kNm ( = 0.6Mp)
以上から大梁の曲げモーメントは下に示す通りであり降伏点として仮定したA点、D点、B点以外は降伏モーメント以下となっており、降伏条件を満たしている。
【 別解 】
崩壊メカニズムー3を真の崩壊メカニズム時と仮定すると、Pu = 282kNであることから外力分布は以下の通りとなる。
ここで、降伏の順番を考慮し、梁A-Bを両端ピン支持の梁と仮定した場合の左右の支点反力及び曲げモーメントを求める。左右の支点反力をそれぞれRA、RBとすると、カの釣り合いから以下の式が成り立つ。
RA + RB = 282 + 564 = 846
A点廻りのモーメントのつり合いから、
282 × 2 + 564 × 4 = 6 × RB
RA = 376kN、RB = 470kN
ここで得られた支点反力をもとに両端支持と仮定した梁の曲げモーメントは
MC = 376 × 2 = 752 kNm
MD = 470 × 2 = 940 kNm
と求められる。
以上の結果より両端支持と仮定した梁の曲げモーメントは以下の通りである。
曲げ応力図としては、この状態に両端にMpが作用している状態を重ね合わせる。
実際には左右端は固定端であるため、両端にヒンジが発生する場合は固定端モーメントによる曲げ戻しが発生する。
終局時の応力は両端支持と仮定した梁の曲げモーメントと固定端モーメントの足し合わせとなる。
以上から大梁の曲げモーメントは上に示す通りであり、降伏点として仮定したA点、D点、B点以外は降伏モーメント以下となっており、降伏条件を満たしている。
(このことから下界定理を満たすことも確認でき、解の唯一性定理が成立している。)
[ No.4 ]
次の枠内の文章の欄 [ ① ] 及び [ ② ] の中の2つの語句のうち、いずれか適切なものを選択せよ。
答え
[ 解答 ]
[ No.2 ]で用いた仮想仕事法による計算は上界定理に基づいている。上界定理とは、そこで示した条件を満たす解Λuは真の解 ΛT以上の値となる(Λu ≧ ΛT)というものである。そのため、この設問で云う得られた崩壊荷重は真の崩壊荷重に対して大きな値となることがある(解説補足では、崩壊メカニズムー2 と仮定すると Pu= 352.5 kNとなり、真の崩壊荷重 Pu= 282 kNよりも大きくなることを示している)。そのため、真の崩壊荷重に対して過大評価することになり、骨組の耐力を危険側に見積もる結果となる。
① 過大
② 危険側
【 解説補足 】
仮に崩壊メカニズムー2を真の崩壊メカニズム時と仮定すると、( [ No.2] (b)より、)
Pu =1.5 Mp/L
= 1.5 × 470 /2.0
= 352.5 kN
であることから外力分布は以下の通りとなる。
別解と同様にして、
ここで、梁A-Bを両端支持の梁と仮定した場合の曲げモーメントを求める。左右の反力をそれぞれRA、RBとすると、力の釣り合いから以下の式が成り立つ。
RA + RB = 352.5 + 705 = 1057.5
352.5 × 2 + 705 × 4 = 6 × RB
RA = 470kN、RB = 587.5kN
ここで得られた支点反力をもとに両端支持と仮定した梁の曲げモーメントは
Mc = 470 × 2 = 940 kNm
MD = 587.5 × 2 = 1175 kNm
で求められる。以上の結果より両端支持と仮定した梁の曲げモーメントは以下の通りである。
実際には左右端は固定端であるため、両端にヒンジが発生する場合は固定端モーメントによる曲げ戻しが発生する。
終局時の応力は両端支持と仮定した梁の曲げモーメントと固定端モーメントの足し合わせとなる。
以上から大梁の曲げモーメントは上に示す通りである。
ただし、この解ではD点の曲げモーメントが降伏モーメント以上( 1.5Mp )となっており、降伏条件を満たしていない。すなわち下界の定理が成立していない。
この記事へのトラックバックURL
https://fanblogs.jp/tb/12626333
※ブログオーナーが承認したトラックバックのみ表示されます。