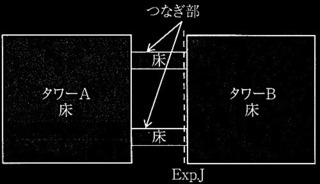
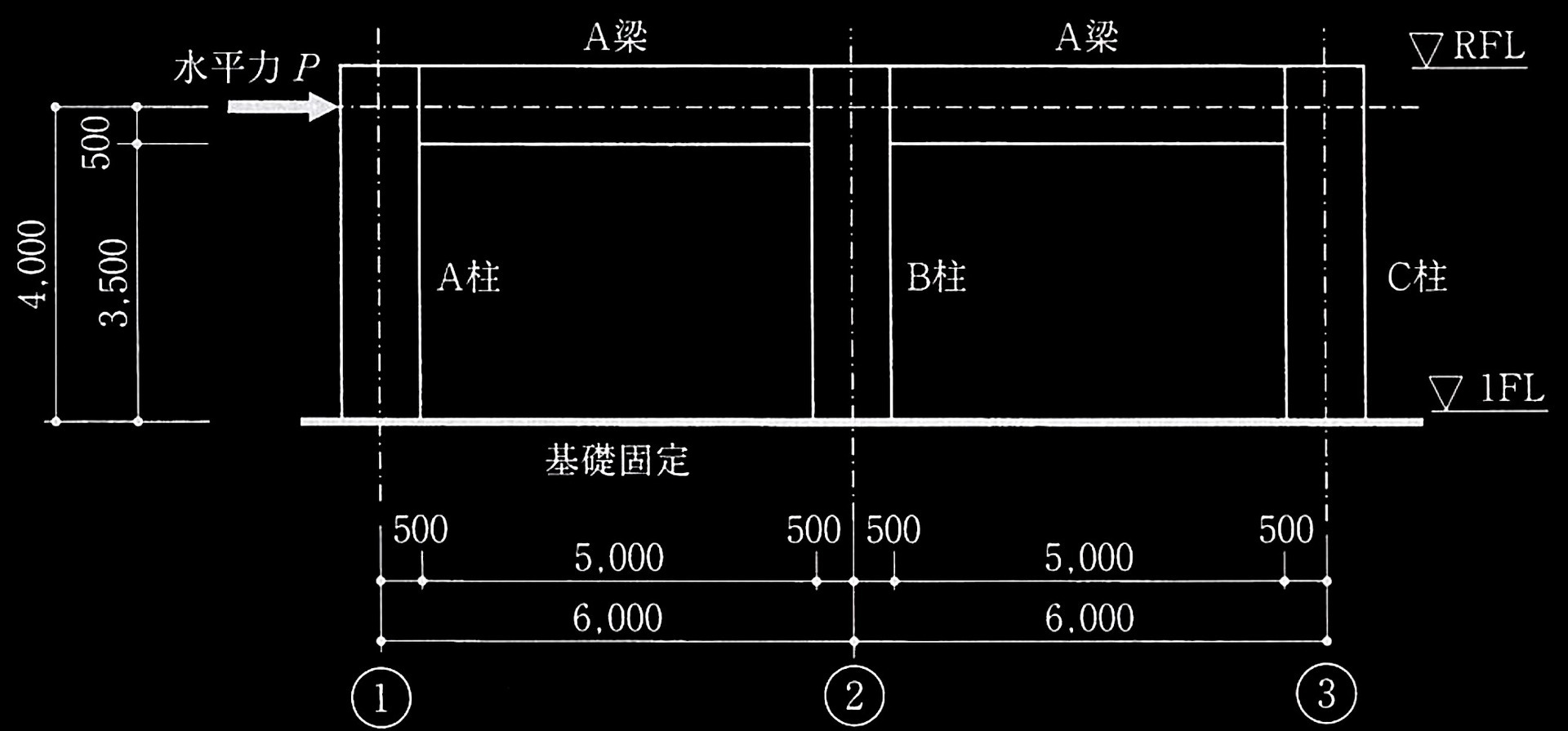
�S�R���N���[�g�����z���̑ϐk�v�Z���[�g3�Ɋւ��āA�}1�Ɏ����ϗ͕ǂ̂Ȃ����߉ˍ\�ɍ������琅����P����p�����ꍇ�ɂ��āA�ȉ��̐ݖ�ɉ���B�����d�y�ю������͂ɂ��e���͖���������̂Ƃ��A�Y���q���W����������\��������ʒu����}2�Ɏ����B�܂��A������P�ɂ��Ȃ����[�����g�}�̈���}3�Ɏ����B
�@�@�@�@�@�@�@�}1 �ˍ\�̎��g�}�i�P�ʁFmm)
�@�@�@�@�@�@
�@�@�@�@�@�@�@�}2 �Y���q���W�̑z��ʒu
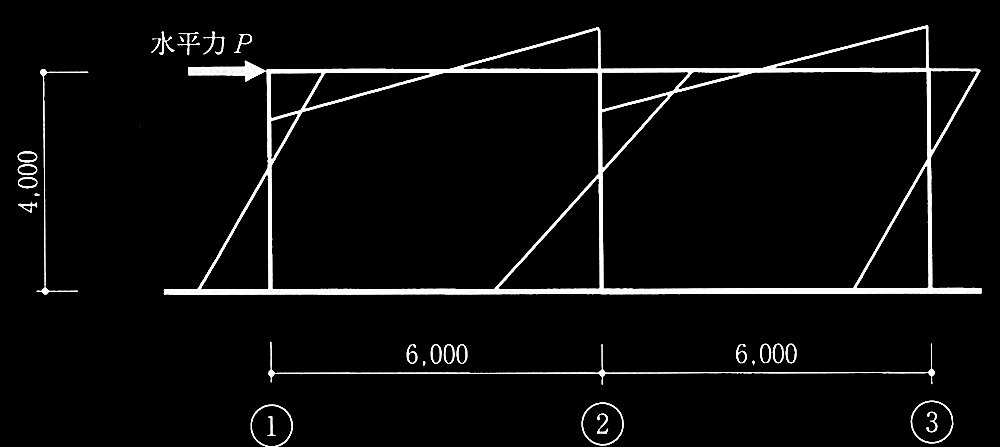
�@�@�@�@�@�@�@�}3 �Ȃ����[�����g�}�̈��i�P�ʁFmm)
������P�ɂ��ˍ\�̕���`���`�������ꍇ�A�Y���q���W�̔����͉��L�́����̑��̏���������(�) �ɏ]���Ĕ��肷����̂Ƃ���B�܂��A���ނ̎�ʂ́����̑��̏���������(�)�ɏ]���Ĕ��肷����̂Ƃ���B
�����̑��̏�������
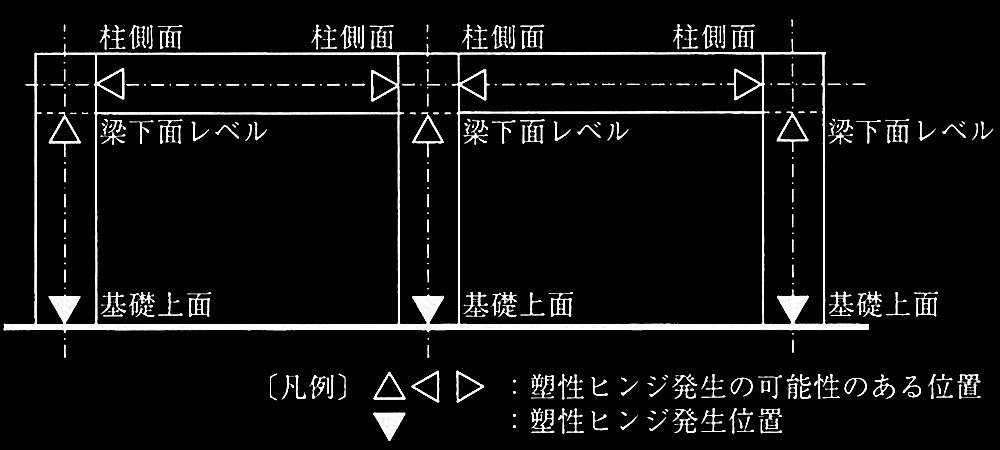
(�) �Y���q���W�̔����́A�ߓ_�ʒu�ɂ�����Ȃ����[�����g�i�ߓ_�Ȃ����[�����g�j��p���āA��(1)�A���邢�͎�(2)�ɂ�蔻�肷��B�Ȃ��A����ɗp����e���ނ̐ߓ_�Ȃ����[�����g�́A���ނ̂���f�͂����Ƃ��āA�}2�Ɏ������ނ̗��[���ɑY���q���W�����肵�ċȂ��I�ǃ��[�����g(Mu)����Z�肵�Ă悢�i�}5�Q�Ɓj�B�����ŁAgMu�͗��̐ߓ_�Ȃ����[�����g�A��gMu�͐ߓ_�܂��̗��̐ߓ_�Ȃ����[�����g�̘a�AcMu�͒��̐ߓ_�Ȃ����[�����g�������B
�E�ߓ_�܂��̗��[���ɑY���q���W����
�@��gMu �� cMu�@�@��(1)
�E�������ɑY���q���W����
�@��gMu > cMu�@�@��(2)
(�) ���ނ̎�ʂ́A�Y���q���W�̔����ɉ����āA����f�I�Ǒϗ�(Qsu)������`�`�����̂���f��(QM)�ɑ��āA��(3)�A���邢�͎�(4) ������ꍇ�ɂ�FA�A�������Ȃ��ꍇ�ɂ�FD�Ƃ���B�Ȃ��A�j��`���������A�e���ނɂ����ď��a55�N���ݏȍ�����1792����4�̎�ʂɊւ��鏔���l�͋K��l�����Ă�����̂Ƃ��Ă悢�B
�E���ނ̗��[�Ƀq���W����������
�@�@Qsu �� 1.10 QM�@�@��(3)
�E��L�ȊO�̏��
�@�@Qsu �� 1.25 QM�@�@��(4)
[ No.1 ]
R�K��A���͗����X���u�t�����iT�`���j�ł���A�X���u���������ɂȂ�Ȃ��I�ǃ��[�����g�́A�L�������̃X���u�ɂ��傫���e�������BA���̋Ȃ��I�ǃ��[�����g�y�ю�ʂɊւ��鎟�̇@�`�B�̐ݖ�ɉ���B���̍ہAA���̋Ȃ��I�ǃ��[�����gMu �͎�(5) �ɂ����̂Ƃ���B�����ł́AT�`���̗L�������͒����`���̗L�������Ɠ��������̂Ƃ��Ă悢�BA���̈�������AA����Mu�ɍl������������X���u��}4�Ɏ����B�f��1 �ł͕Б��� 1m���̃X���u�A�f��2�ł͕Б��X�p���̖��ɑ������镝�̃X���u��L���Ƃ���B�܂��AA���y��A���̗��[���ɑY���q���W�����������ꍇ�̋Ȃ����[�����g�}��}5�Ɏ����B
�@Mu = 0.9(at + as) �Es��y�Ed�@�@��(5)
�����ɁA
�@Mu�F���̋Ȃ��I�ǃ��[�����g(N�Emm)
�@at�F���̈�������̒f�ʐρimm2)
�@as�F�L�������̈������X���v�̒f�ʐ�(mm2)
�@s��y �F��؋y�уX���u�̍ޗ����x(N/mm2)�ŁA325 N/mm2�Ƃ��Ă悢�B
�@d�F�����`���y��T�`���̗L������(mm)�ŁA920mm�Ƃ��Ă悢�B
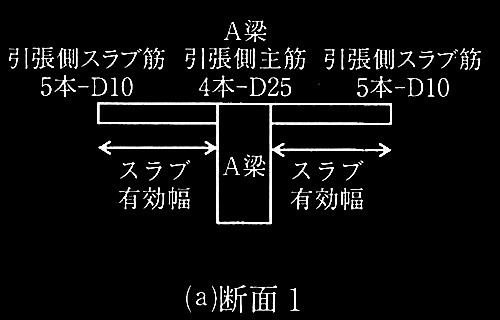
(a) �f��1
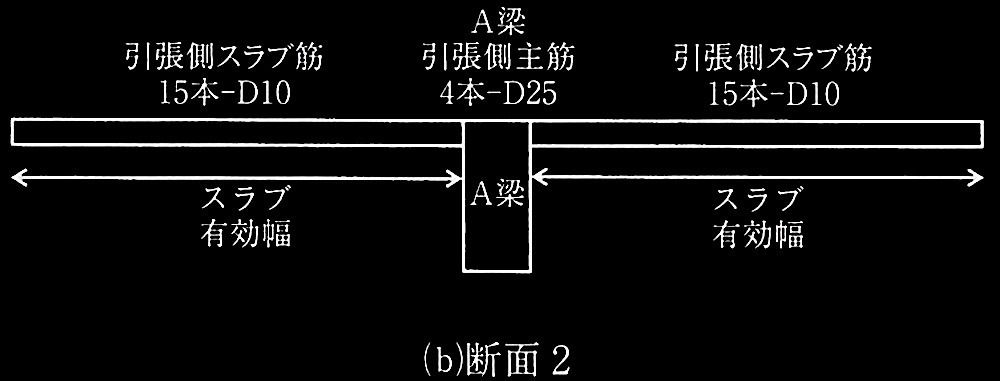
(b) �f��2
���ʎ����F
���(D25)1�{�̒f�ʐρF507mm2
�X���u��(D10)1�{�̒f�ʐρF71 mm2
�}4 A���̈�������؋y�їL�������̈������X���u��
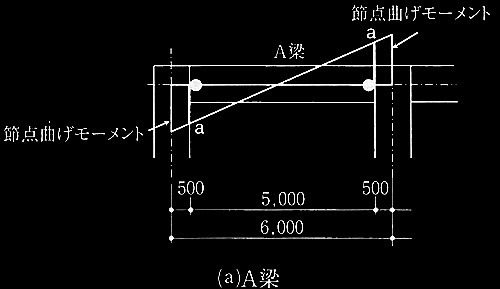
�}5 ���ޗ��[���ɑY���q���W�����������ꍇ�̋Ȃ����[�����g
�@ �X���u���������ɂȂ�ꍇ�A�����`���Ƃ��Ă�Mu (Muo)�ɑ���f��1��T�`����Mu(Mu1)�̔䗦(Mu1/Muo)�����߂�B�Ȃ��A�����`���̈�������͐}4�Ɏ���A���̈�������ł���B
����
�Ȃ��I�ǃ��[�����g�͎�(5)��p���Ă��ꂼ��ȉ��̂悤�ɋ��߂�B
�����`���Ƃ��Ă̋Ȃ��I�ǃ��[�����g�́A
�@Mu(Muo) = 0.9 × (4 × 507)�E s��y�Ed
�f��1��T�`���̋Ȃ��I�ǃ��[�����g�́A
�@Mu(Mu1) ��0.9 × (4 × 507 + 10 × 71)�Es��y�Ed
����āA
Mu1/Muo = (4 × 507+10 × 71)/ (4 × 507)
�@�@�@�@= 1.35
�ƂȂ�B
�A �X���u���������ɂȂ�ꍇ�A�f��1��T�`����Mu (Mu1)�ɑ���f��2��T�`����Mu(Mu2)�̔䗦(Mu2/Mu1)�����߂�B
����
���l�ɒf��2��T�`���̋Ȃ��I�ǃ��[�����g�́A
Mu(Mu2) = 0.9 × (4 × 507 + 30 × 71)�Es��y�Ed
����āA
Mu2/Mu1 = (4 × 507 + 30 × 71)/(4 × 507 + 10 × 71)
�@�@�@�@ = 1.52
�ƂȂ�B
�B A���̗��[���ɑY���q���W�����������ꍇ�i�}5 (a)�j�ɂ��āAA���̎�ʂ肵�A��ʔ���̍������Ȍ��ɋL�q����B�����ŁAA�����[���̑Y���q���W�̋Ȃ��I�ǃ��[�����gMu�� a(kN�Em)�AA���̂���f�I�Ǒϗ�Qsu��0.60 a(kN)�Ƃ���B
����
A���̗��[�ɑY���q���W�����������̂���f�͂́AA���̓��@������ 5m�Ȃ̂ŁA
�@QM = 2 × a/5 = 0.40a (kN)
A���̎�ʂ́A���[�ɑY���q���W�������Ă���̂Ŏ�(3)�ɂ�蔻�肷��ƁA
�@Qsu = 0.60a (kN) �� 1.10QM = 1.10 × 0.40a = 0.44a (kN)
����āA��(3)�����Ă���̂�A���̎�ʂ�FA�ł����B
�Ȃ��A�����ł͖�蕶�Ɂu�����d�y�ю������͂ɂ��e���͖�������v�Ƃ���̂ŁAA���̏펞�̉����d�ɂ�邹��f�͖͂������Ă���B
[ No.2 ]
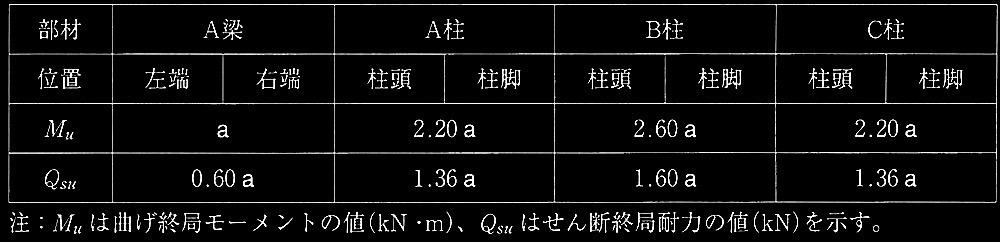
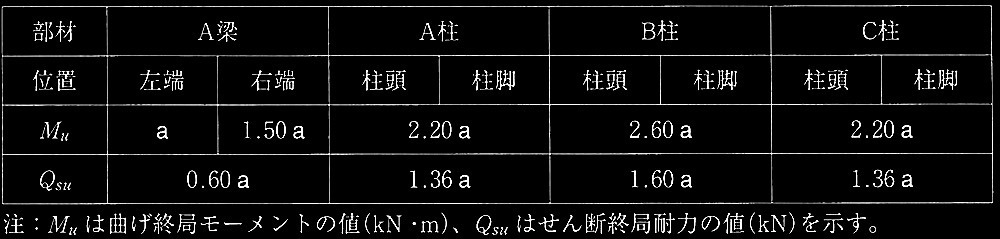
������P�̑���ɂ��A�ˍ\�̕���`���`�������B�e���ނ̑ϗ͂��\1�Ɏ����l�ƂȂ�P�[�X�T �ɂ��āA�ۗL�����ϗ͋y�э\�������W�����Ɋւ��鎟�̇@�`�B�̐ݖ�ɉ���B
�\1 ���ނ̑ϗ́i�P�[�X�T �j
�@ �ˍ\�̕���`�ɂ��āA�Y���q���W�̔����ʒu���p���̃t���[���}�Ɂ��Ŏ����B���̍ہA�}5���Q�l�ɁA�Y���q���W���������Ă��镔�ނ̒[���Ɂ���\�L����B
����
�y�i��j�z
������P�̑���ɂ��AA���[�܂���A�EB�EC�������̂ǂ���ɑY���q���W�������邩�́A�ߓ_�ʒu�ɂ�����Ȃ����[�����g�̒ނ荇�����画�f����B�]���āA�������y�ї��[���̊댯�f�ʈʒu�ɑY���q���W�����肵�āA���̏ꍇ�̕��ނ̂���f�͂���ߓ_�Ȃ����[�����g���Z�o����B���ɒ��y�ї����̐ߓ_�Ȃ����[�����g�̑��a�̏��������̕��ށi�����͗��j�ɑY���q���W��ݒ肵�āA�Y���q���W�������Ȃ����ނ̐ߓ_�Ȃ����[�����g���C�����A���̒l���畔�ނ̂���f�͂��C������i�����̑��̏�������(�)�ɂ��j�B
�쐬��������`�`�����̋Ȃ����[�����g�E����f�͐}���ȉ��ɋL�ڂ���B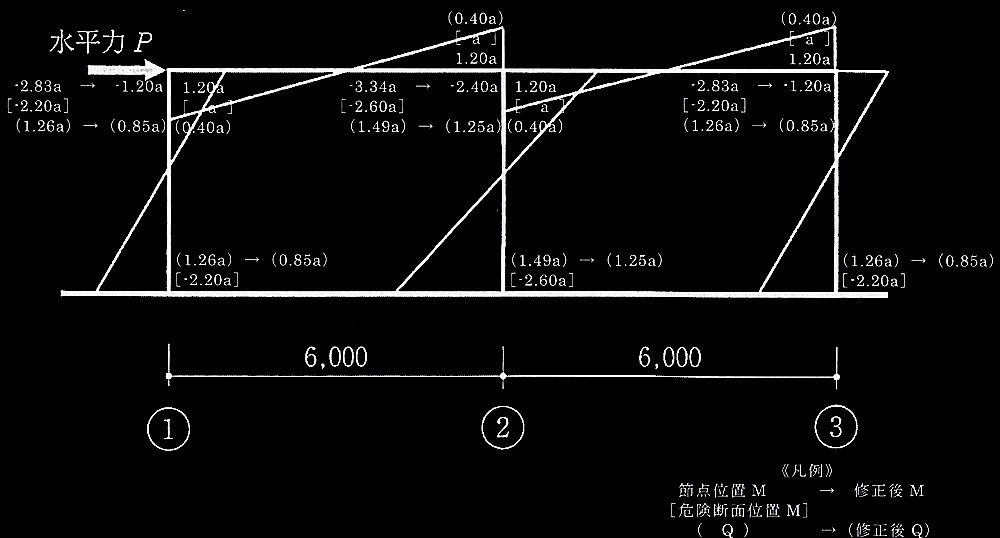
�ˍ\�̕���`�͈ȉ��̐}�ƂȂ�B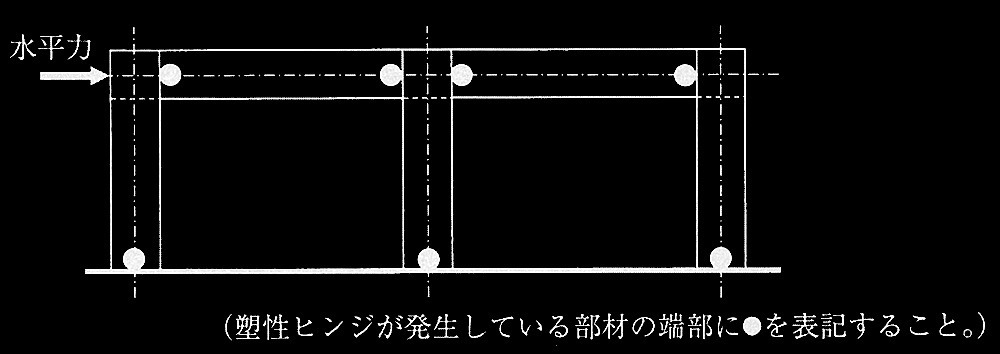
�A �ˍ\�ۗ̕L�����ϗ́i����`�`�����̐�����P�T �j��\1�Ɏ���a��p���ē�����B
����
�ˍ\�ۗ̕L�����ϗ�P1�͕���`�`�����̒��̂���f�͂̍��v�ƂȂ�̂ŁA
�@P �T = 0.85a + 1.25a + 0.85a = 2.95a (kN)
�B 1�K����L�̕���`���`������A���AB���y��C������\�������ꍇ�A1�K�̍\�������W�� Ds�����a55�N���ݏȍ�����1792����4�ɏ]���ċ��߁A���̍������Ȍ��ɋL�q����B
����
�悸A���AA���AB���y��C���̎�ʂ肷��B�����ŁAA���ɂ͗��[�Ƀq���W�������Ă���̂Ŏ�(3)�AA���AB���y��C���͒����Ƀq���W�������Ă��Ȃ��̂Ŏ�(4)�ɂĔ��肷��B�Ȃ��A�����ł͖�蕶�Ɂu�j��`���������A�e���ނɂ����ď��a55�N���ݏȍ�����1792����4�̎�ʂɊւ��鏔���l�͋K��l�����Ă�����̂Ƃ��Ă悢�B�v�Ƃ���̂ŁA��(3)�y�ю�(4)�ɂ��j��`���݂̂ɂĎ�ʂ肷��B
A���F
�@Qsu = 0.60a (kN) �� 1.10QM
�@�@�@�@�@�@�@�@�@= 1.10 x 0.40a = 0.44a (kN)
�@�� FA
A���y��C���F
�@Qsu = 1.36a (kN) �� 1.25QM
�@�@�@�@�@�@�@�@�@= 1.25 × 0.85a
�@�@�@�@�@�@�@�@�@= 1.06a (kN)
�@�� FA
B�� �FQsu = 1.60a (kN) �� 1.25QM
�@�@�@�@�@�@�@�@�@�@�@ = 1.25 × 1.25a
�@�@�@�@�@�@�@�@�@�@�@ = 1.56a (kN)
�@�� FA
��L���A���AB���y��C���̐����ϗ͂͑S�Ď��FA�ł��钌�̑ϗ͂ƂȂ�̂ŁA1�K�̕��ތQ�Ƃ��Ă̎�ʂ�A�ƂȂ�B�]���āA 1�K�̍\�������W��Ds��0.30�ƂȂ�B
[ No.3 ]
�ˍ\�̕ό`�ɂ��T�`���̃X���u�̗L���������傷��ƁA�X���u���������ƂȂ�A���̉E�[��Mu �����傷��B�e���ނ̑ϗ͂��\2�Ɏ����l�ƂȂ�P�[�XII�iA���E�[�ȊO�̓P�[�X I �Ɠ����j�ɂ��āA�ۗL�����ϗ͋y�ѕ��ގ�ʂɊւ��鎟�̇@�y�чA�̐ݖ�ɉ���B
�\2 ���ނ̑ϗ́i�P�[�XII�j
�@ �ˍ\�ۗ̕L�����ϗ́i����`�`�����̐�����P�U �j��\2�Ɏ���a��p���ē�����B
����
�ݖ�[No.2]�Ɠ��l�̕��@�ɂč쐬��������`�`�����̋Ȃ����[�����g ����f�͐}���ȉ��ɋL�ڂ���B�Ȃ��A����`�`�����̑Y���q���W�����ʒu�͐ݖ�mNo.2]�̌��ʂƓ����ł���B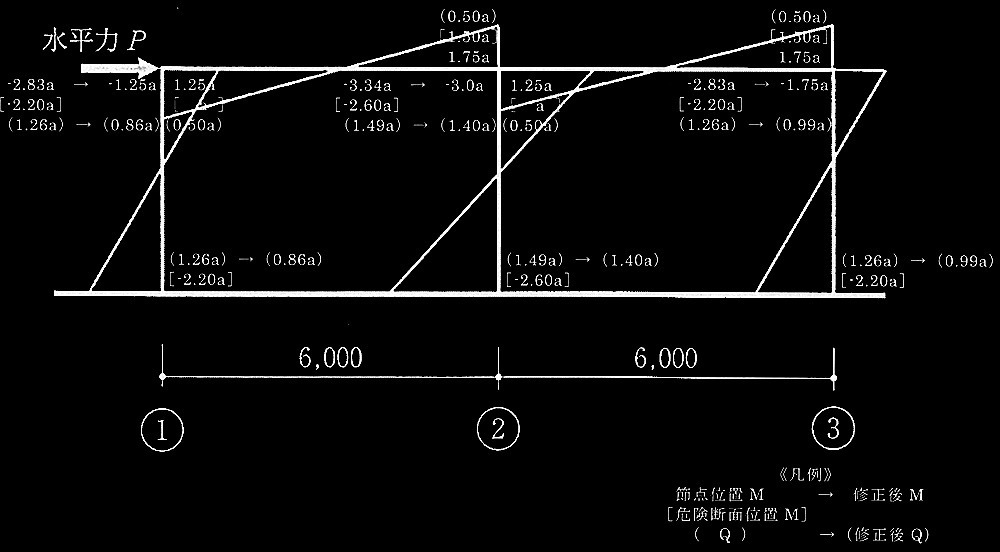
�ˍ\�ۗ̕L�����ϗ͂�P�U�͕���`�`�����̒��̂���f�͂̍��v�ƂȂ�̂ŁA
�@P�U = 0.86a + 1.40a + 0.99a
�@�@�@= 3.25a (kN)
�A B���̎�ʂ肵�A��ʔ���̍������Ȍ��ɋL�q����B
����
B���̎�ʂ͒����Ƀq���W�������Ă��Ȃ��̂Ŏ�(4)�ɂĔ��肷��B
�@Qsu = 1.60a (kN) < 1.25QM
�@�@�@�@�@�@�@�@�@= 1.25 × 1.40a
�@�@�@�@�@�@�@�@�@= 1.75a (kN)
����āA��(4)�����Ă��Ȃ��̂ŁA����f�j��`���̕��ނƂȂ�A
��ʂ�FD�Ɣ��肷��B
-
no image