2015�N04��18��
0025.�@�C���^�[�o���̓]���̓x��
������B��������ł��ׂ͂���(灬╹��╹灬)�ł�
���͓]���Ƃ����l�����ɂ��Ăł�
�]���Ƃ́A
���Ƃ��A
�y�h���猩���\�z�̃C���^�[�o����
�@��Perfect�T�ɂȂ�܂����A
���̃h��1�I�N�^�[�u�グ��
�y�\���猩���h�z�̃C���^�[�o�����l�����
�@��Perfect�S�ɂȂ�܂�
���̂悤�ȁA
�y�h���\�z�Ɓy�\���h�z�̂悤��
�I�N�^�[�u�����ւ�������ꂽ������
�]���Ƃ����܂�
�]�������Ȃ̂Ńv�v�b (�Pm�P*�j
�y�X�|���T�[�����N�z
�����̊W�ɂ͎��̂悤�ȃ��[��������܂�
���̕\�́A���ꂼ��]���̊W�ɂȂ��Ă�����̂��ŋ����Ă���܂�
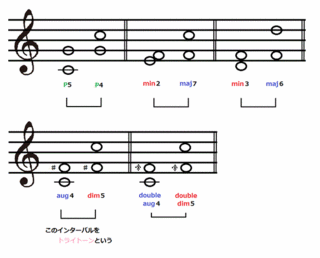
�������͓x���B�����͑����Ɓu�X�v�ɂȂ�
��j
Perfect�T��Perfect�S�ł�����
���ꂼ��̓x���A�T�ƂS�𑫂���9�ɂȂ�
Point!!
�܂�A�]���̓x����m�肽���Ƃ���
�X����A���̓x���������Z���܂�
����Perfect�y�T�z�Ȃ�B
�]����m�肽���̂ŁA
�u�X����A���̓x���y�T�z�������ĂS�v
���Ȃ̂œ]���́uPerfect�S�v�ƂȂ�܂�
���Ӂj
���܂��APerfect�ȊO�̃C���^�[�o������
�]���Ɉڍs����ۂ��̃��[���ŕω����܂�
���j
major�R�̓]���́H
�������j
�@�y�]���̓x����9��������z
���@�X�[�R�@���@�y�U�z
�A�yPerfect�ȊO�̖��O�͕ϊ�����z
major�́@���@�yminor�z�ɂȂ�
�����major�R�̓]����
minor�U�@�ƂȂ�B
����͊o���Ă���
�C���^�[�o���̌v�Z���y�ɂȂ�̂ŕ֗��ł�
(���L䇁M)�t�J�n�b
�Ȃ��A�C���^�[�o���̂��ڂ����Ƃ���
�O�ɏЉ��
C major scale�𗘗p�������̂Ƃ͕ʂ�
���̖@�����ۈËL�����
�ƂĂ������C���^�[�o�����v�Z�ł���̂�
������Ƒ�ςł����A���ڂ��Ă݂Ă�������
�]���𗘗p���Ċo�����
���ڂ���ʂ͔����ōςނ̂ŁA
���C���^�[�o�����g�����Ȃ��������Ƃ���
���Ў��̊ۈËL�ɒ��킵�Ă݂Ă�������
�_�i���O�ցO���j�^
���ڂ������̃R�c
�@��A�������̂������m���ɂ��ڂ���
�i��A��͂��Ƃŕϊ�����Ƃ��Ɏg���j
�����������\�ł܂Ƃ߂Ă����܂����B
�A�]���̂ǂ����������܂��m���ɂ��ڂ���
�i�]�T������ǂ��炩�����ڂ��Ă����j
Perfect�͎g�p�p�x�I��
�T�x�̂ق��ł��ڂ����ق����悢����
�ł́A�ǂ���������������
�@Perfect�S�@�Ɓ@Perfect�T
Point!!
��A��̂Ȃ�Perfect�S�APerfect�T��
B��F�@diminish�T
F��B�@augment�S�̂Q�ɋC�������
���ڂ���̂͂���
�A�Rrd�C���^�[�o����6th�C���^�[�o��
Point!!
�C���^�[�o���̘b���I�������
���̓R�[�h�̘b�ɂ͂��邯�ǁA
�Ƃ��ɂRrd�C���^�[�o����
���ڂ��Ă����ƌ��ʓI
���ڂ������̃R�c��
major�Aminor���킯�邱��(���L�́M)�m+�K
�B�Qnd�C���^�[�o���ƂVth�C���^�[�o��
Point!!
2nd�͔����������͑S���̊Ԋu�Ȃ̂�
���ڂ��₷���ł�
�R�[�h�̂��Ƃ��v����
7th�ł��ڂ���̂��֗��ł�
���W���[���Q�������Ă��ڂ���Ƃ���
�ȏ�ł�
�܂��͇@�A�B��
���ꂼ��ǂ��炩��������ڂ��Ă݂Ă�
�������߂�
3rd�A5th�A7th�ł�
����3�킪���S�ɔc���ł��Ă����
���̃R�[�h�̘b
���������ł���(�P�[�P)��د
�ł���������1��
�C���^�[�o���̘b�����܂����߂�您��������
���͓]���Ƃ����l�����ɂ��Ăł�
�]���Ƃ́A
���Ƃ��A
�y�h���猩���\�z�̃C���^�[�o����
�@��Perfect�T�ɂȂ�܂����A
���̃h��1�I�N�^�[�u�グ��
�y�\���猩���h�z�̃C���^�[�o�����l�����
�@��Perfect�S�ɂȂ�܂�
���̂悤�ȁA
�y�h���\�z�Ɓy�\���h�z�̂悤��
�I�N�^�[�u�����ւ�������ꂽ������
�]���Ƃ����܂�
�]�������Ȃ̂Ńv�v�b (�Pm�P*�j
�y�X�|���T�[�����N�z
�����̊W�ɂ͎��̂悤�ȃ��[��������܂�
���̕\�́A���ꂼ��]���̊W�ɂȂ��Ă�����̂��ŋ����Ă���܂�

�������͓x���B�����͑����Ɓu�X�v�ɂȂ�
��j
Perfect�T��Perfect�S�ł�����
���ꂼ��̓x���A�T�ƂS�𑫂���9�ɂȂ�
Point!!
�܂�A�]���̓x����m�肽���Ƃ���
�X����A���̓x���������Z���܂�
����Perfect�y�T�z�Ȃ�B
�]����m�肽���̂ŁA
�u�X����A���̓x���y�T�z�������ĂS�v
���Ȃ̂œ]���́uPerfect�S�v�ƂȂ�܂�
���Ӂj
���܂��APerfect�ȊO�̃C���^�[�o������
�]���Ɉڍs����ۂ��̃��[���ŕω����܂�
major�@�́@minor augment�@�́@diminish �@�@double augment�@�́@double diminish�@�@ |
���j
major�R�̓]���́H
�������j
�@�y�]���̓x����9��������z
���@�X�[�R�@���@�y�U�z
�A�yPerfect�ȊO�̖��O�͕ϊ�����z
major�́@���@�yminor�z�ɂȂ�
�����major�R�̓]����
minor�U�@�ƂȂ�B
����͊o���Ă���
�C���^�[�o���̌v�Z���y�ɂȂ�̂ŕ֗��ł�
(���L䇁M)�t�J�n�b
�Ȃ��A�C���^�[�o���̂��ڂ����Ƃ���
�O�ɏЉ��
C major scale�𗘗p�������̂Ƃ͕ʂ�
���̖@�����ۈËL�����
�ƂĂ������C���^�[�o�����v�Z�ł���̂�
������Ƒ�ςł����A���ڂ��Ă݂Ă�������
�]���𗘗p���Ċo�����
���ڂ���ʂ͔����ōςނ̂ŁA
���C���^�[�o�����g�����Ȃ��������Ƃ���
���Ў��̊ۈËL�ɒ��킵�Ă݂Ă�������
�_�i���O�ցO���j�^
���ڂ������̃R�c
�@��A�������̂������m���ɂ��ڂ���
�i��A��͂��Ƃŕϊ�����Ƃ��Ɏg���j
�����������\�ł܂Ƃ߂Ă����܂����B
�A�]���̂ǂ����������܂��m���ɂ��ڂ���
�i�]�T������ǂ��炩�����ڂ��Ă����j
Perfect�͎g�p�p�x�I��
�T�x�̂ق��ł��ڂ����ق����悢����
�ł́A�ǂ���������������
�@Perfect�S�@�Ɓ@Perfect�T
��Perfect�T�@�@�@�@�@(�@)�͔����̐��@ �@C�@��G�@�i�V�j�@Perfect�T �@D�@��A�@�i�V�j�@Perfect�T �@E�@��B�@�i�V�j�@Perfect�T �@F�@��C�@�i�V�j�@Perfect�T �@G�@��D�@�i�V�j�@Perfect�T �@A�@��E�@�i�V�j�@Perfect�T ���Ӂj �@B�@��F�@�i�U�j�@diminish�T |
��Perfect�S�@�@�@�@�@(�@)�͔����̐��@ �@G�@��C�@�i�T�j�@Perfect�S �@A�@��D�@�i�T�j�@Perfect�S �@B�@��E�@�i�T�j�@Perfect�S �@C�@��F�@�i�T�j�@Perfect�S �@D�@��G�@�i�T�j�@Perfect�S �@E�@��A�@�i�T�j�@Perfect�S ���Ӂj �@F�@��B�@�i�U�j�@augment�S |
Point!!
��A��̂Ȃ�Perfect�S�APerfect�T��
B��F�@diminish�T
F��B�@augment�S�̂Q�ɋC�������
���ڂ���̂͂���
�A�Rrd�C���^�[�o����6th�C���^�[�o��
���Rrd�@�@�@�@�@�@�@(�@)�͔����̐��@ ���W���[�n �@C�@��E�@�i�S�j�@major�R �@�e�@��A�@�i�S�j�@major�R �@G�@��B�@�i�S�j�@major�R �}�C�i�[�n �@�c�@��F�@�i�R�j�@minor�R �@E�@��G�@�i�R�j�@minor�R �@A�@��C�@�i�R�j�@minor�R �@B�@��D�@�i�R�j�@minor�R |
���Uth�@�@�@�@�@�@�@(�@)�͔����̐��@ �}�C�i�[�n �@E�@��C�@�i�W�j�@minor�U �@A�@��F�@�i�W�j�@minor�U �@B�@��G�@�i�W�j�@minor�U ���W���[�n �@F�@��D�@�i�X�j�@major�U �@G�@��E�@�i�X�j�@major�U �@C�@��A�@�i�X�j�@major�U �@D�@��B�@�i�X�j�@major�U |
Point!!
�C���^�[�o���̘b���I�������
���̓R�[�h�̘b�ɂ͂��邯�ǁA
�Ƃ��ɂRrd�C���^�[�o����
���ڂ��Ă����ƌ��ʓI
���ڂ������̃R�c��
major�Aminor���킯�邱��(���L�́M)�m+�K
�B�Qnd�C���^�[�o���ƂVth�C���^�[�o��
���Vrd�@�@�@�@�@�@�@(�@)�͔����̐��@ ���W���[�n �@C�@��B�@�i11�j�@major�V �@F�@��E�@�i11�j�@major�V �}�C�i�[�n �@D�@��C�@�i10�j�@minor�V �@E�@��D�@�i10�j�@minor�V �@G�@��F�@�i10�j�@minor�V �@A�@��G�@�i10�j�@minor�V �@B�@��A�@�i10�j�@major�V |
���Qnd�@�@�@�@�@�@�@(�@)�͔����̐��@ �}�C�i�[�n �@E�@���e�@�i�P�j�@minor�Q �@B�@���b�@�i�P�j�@minor�Q �@ ���W���[�n �@C�@��D�@�i�Q�j�@major�Q �@D�@��E�@�i�Q�j�@major�Q �@F�@��G�@�i�Q�j�@major�Q �@G�@��A�@�i�Q�j�@major�Q �@A�@��B�@�i�Q�j�@major�Q |
Point!!
2nd�͔����������͑S���̊Ԋu�Ȃ̂�
���ڂ��₷���ł�
�R�[�h�̂��Ƃ��v����
7th�ł��ڂ���̂��֗��ł�
���W���[���Q�������Ă��ڂ���Ƃ���
�ȏ�ł�
�܂��͇@�A�B��
���ꂼ��ǂ��炩��������ڂ��Ă݂Ă�
�������߂�
3rd�A5th�A7th�ł�
����3�킪���S�ɔc���ł��Ă����
���̃R�[�h�̘b
���������ł���(�P�[�P)��د
�ł���������1��
�C���^�[�o���̘b�����܂����߂�您��������
���̋L���ւ̃R�����g
�R�����g������
���̋L���ւ̃g���b�N�o�b�NURL
https://fanblogs.jp/tb/3559144
���u���O�I�[�i�[�����F�����g���b�N�o�b�N�̂ݕ\������܂��B
���̋L���ւ̃g���b�N�o�b�N