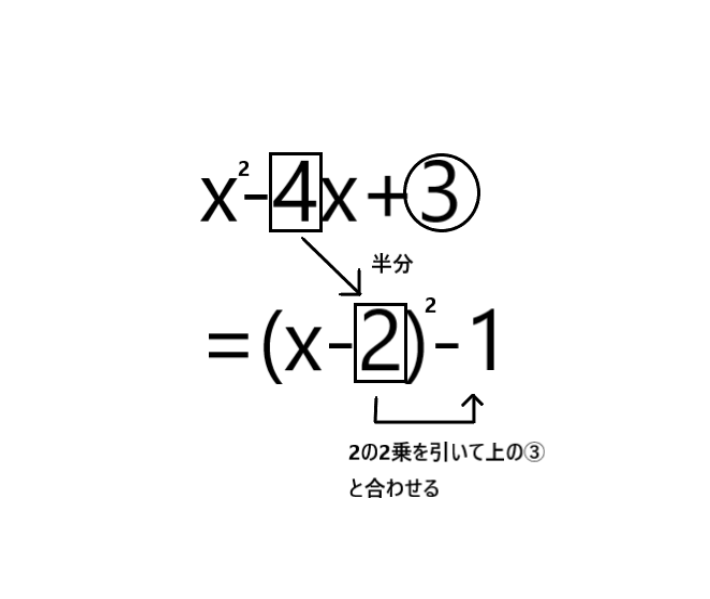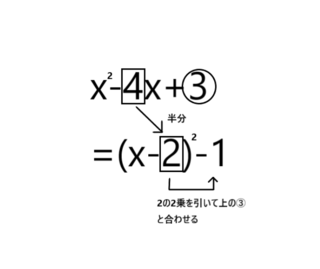2021�N09��06��
���w�̏ꍇ�̐��Ɗm���͂Ȃ�����̂�
����ɂ���
�v���Ԃ�̓��e�ɂȂ�܂�
����́A���wA�ŊF����J����u�ꍇ�̐��v�Ɓu�m���v�ɂ��Ęb���܂��B
�������A����͋��ӎ�����菜�����Ƃ��ӎ����Ęb���Ă�������Ǝv���܂��B
�ł́A
�ꍇ�̐��Ɗm���͎��͍��Z���ŏ��߂ďK���܂����Č����l�͎��͂���قǂ��Ȃ���ł��B
�v���o���Ă݂Ă��������I
�ق�A���w�Z�̍Ō�̕��A���w�Z�A�Ƃ���ǂ���ŏK���Ă���͂��I
�����I���C�}�ł��B�ׂ��������A���Z�����ł����������̘b������ł��܂���ˁB
���͓y��͍���Ă���̂ł��B
����Ȃ̂ɁA�ǂ����č��Z�ŏK�����̂Ɋւ��Ắu����v�Ɗ����Ă��܂��̂ł��傤���H
����́A�Y�o���A�������ɖ�肪����Ǝ��͎v���܂��I
�����炭�A���Z�Ŏ��`�}����鎖���ď��Ȃ��Ǝv����ł���B�ł��A���ꂪ��{�Ȃ̂ŁA������ӎ����鎖����������Ȃ�ł��B
�ӎ����Ȃ��ŁA
���Z�łȂ炤�uP�v��uC�v��u�I�v�Ȃ�ċL�����苳����Ă��܂��ƁA�ǂ��Ȃ�܂��H
�����ł��B
���������A���̖��́u��������ĉ����̂��I�v�ƃp�^�[��������悤�ɕ����Ă��܂��̂ł��B
�������ɁA������x�ȒP�Ȗ��Ɋւ��Ă̓p�^�[���ʼn����Ă��܂��܂��B
�������A��{�I�ɂ͂قƂ�ǂ̖�肪�A���߂Č���悤�Ȗ�����̂͂��B
��������A���Z�ŏK�����Ƃ͖��ʂȂ̂ł́H
�Ǝv���Ă̓_���B
���Z�ł́A
���`�}�ł͑�ςȍ�ƂɂȂ�̂��A�K�������������Čv�Z����p���Đ�������̂��I
�Ƃ������Ƃ�����Ă���̂ł��B
�Ȃ̂ŁA���`�}���肫�ŁA�A���̐������Ȃ�uP�v���g�������Ƃ��B
�I�Ԃ����Ȃ�A�uP�v�ł͐��������邩��d����������Z���Ȃ��Ⴂ���Ȃ�����A�uC�v���g�������I
���������ӂ��ɁA���Z�ł͌v�Z�Ő���������̂́u�v�Z�v�ōs���A�����������G�ȏꍇ�́A���`�}�ł�����x���ʂ����悭���Ă���A�c��͌v�Z���g���B�Ƃ����̂��{���̌`�ł��B
�������A���ۂɂ́A�u�ނ��������Ȃ��B�ǂ̋L���g������v�Z�ł���낤�v�čl���Ă邩��A�Y���Ă��ł��B�Ă��A�ނ���S���t�̔��z�ł��B
����Ƃ��́A���`�}�ŏ������ׂĂ����āA�L�����g������v�Z�ł���I�ĂƂ���܂œ����̂ł��B
���Z�ł́A�L��������K���܂�����A���`�}��ʓ|��������l����������̂ł����A�A
�ꍇ�̐��A�m���Ȃ�āu������v�P���Ȃ̂ŁA�������ӎ�����悤�ɂ��܂��傤�B
���ꂾ���ŁA�C�����͂������y�ɂȂ�͂��ł��B
���Ƃ́A�ǂ������������̂Ƃ��ɁA�L�����g����̂����w��ł��������ł��B
��̓I�ɁuP�v��uC�v��u�I�v�͂ǂ��������Ɏg����̂��́A�܂��A�߂������ɘb���čs�����Ǝv���܂��B
�Ō�ɁA���̒P���́u��蕶�������ł���Ƃ��͑�̖̂��͉�����v�͂��ł��B�������̂悤�ɑ��̒P���ƗZ�����Ă���͕̂ʂƂ��āB�B
�Ȃ̂ŁA���ЁA�����ɂȂ炸�A�J��}�X�^�[���Ă��������B
����Љ��̂́A�ȉ��I
����́A�m���̓p�^�[���Ȃ���Ȃ��A������P�����I���Ă������Ƃ��킩�����ɂȂ��Ă܂��B�����Ɏ���Ă݂Ă���������

�v���Ԃ�̓��e�ɂȂ�܂�

����́A���wA�ŊF����J����u�ꍇ�̐��v�Ɓu�m���v�ɂ��Ęb���܂��B
�������A����͋��ӎ�����菜�����Ƃ��ӎ����Ęb���Ă�������Ǝv���܂��B
�ł́A
�ꍇ�̐��Ɗm���͎��͍��Z���ŏ��߂ďK���܂����Č����l�͎��͂���قǂ��Ȃ���ł��B
�v���o���Ă݂Ă��������I
�ق�A���w�Z�̍Ō�̕��A���w�Z�A�Ƃ���ǂ���ŏK���Ă���͂��I
�����I���C�}�ł��B�ׂ��������A���Z�����ł����������̘b������ł��܂���ˁB
���͓y��͍���Ă���̂ł��B
����Ȃ̂ɁA�ǂ����č��Z�ŏK�����̂Ɋւ��Ắu����v�Ɗ����Ă��܂��̂ł��傤���H
����́A�Y�o���A�������ɖ�肪����Ǝ��͎v���܂��I
�����炭�A���Z�Ŏ��`�}����鎖���ď��Ȃ��Ǝv����ł���B�ł��A���ꂪ��{�Ȃ̂ŁA������ӎ����鎖����������Ȃ�ł��B
�ӎ����Ȃ��ŁA
���Z�łȂ炤�uP�v��uC�v��u�I�v�Ȃ�ċL�����苳����Ă��܂��ƁA�ǂ��Ȃ�܂��H
�����ł��B
���������A���̖��́u��������ĉ����̂��I�v�ƃp�^�[��������悤�ɕ����Ă��܂��̂ł��B
�������ɁA������x�ȒP�Ȗ��Ɋւ��Ă̓p�^�[���ʼn����Ă��܂��܂��B
�������A��{�I�ɂ͂قƂ�ǂ̖�肪�A���߂Č���悤�Ȗ�����̂͂��B
��������A���Z�ŏK�����Ƃ͖��ʂȂ̂ł́H
�Ǝv���Ă̓_���B
���Z�ł́A
���`�}�ł͑�ςȍ�ƂɂȂ�̂��A�K�������������Čv�Z����p���Đ�������̂��I
�Ƃ������Ƃ�����Ă���̂ł��B
�Ȃ̂ŁA���`�}���肫�ŁA�A���̐������Ȃ�uP�v���g�������Ƃ��B
�I�Ԃ����Ȃ�A�uP�v�ł͐��������邩��d����������Z���Ȃ��Ⴂ���Ȃ�����A�uC�v���g�������I
���������ӂ��ɁA���Z�ł͌v�Z�Ő���������̂́u�v�Z�v�ōs���A�����������G�ȏꍇ�́A���`�}�ł�����x���ʂ����悭���Ă���A�c��͌v�Z���g���B�Ƃ����̂��{���̌`�ł��B
�������A���ۂɂ́A�u�ނ��������Ȃ��B�ǂ̋L���g������v�Z�ł���낤�v�čl���Ă邩��A�Y���Ă��ł��B�Ă��A�ނ���S���t�̔��z�ł��B
����Ƃ��́A���`�}�ŏ������ׂĂ����āA�L�����g������v�Z�ł���I�ĂƂ���܂œ����̂ł��B
���Z�ł́A�L��������K���܂�����A���`�}��ʓ|��������l����������̂ł����A�A
�ꍇ�̐��A�m���Ȃ�āu������v�P���Ȃ̂ŁA�������ӎ�����悤�ɂ��܂��傤�B
���ꂾ���ŁA�C�����͂������y�ɂȂ�͂��ł��B
���Ƃ́A�ǂ������������̂Ƃ��ɁA�L�����g����̂����w��ł��������ł��B
��̓I�ɁuP�v��uC�v��u�I�v�͂ǂ��������Ɏg����̂��́A�܂��A�߂������ɘb���čs�����Ǝv���܂��B
�Ō�ɁA���̒P���́u��蕶�������ł���Ƃ��͑�̖̂��͉�����v�͂��ł��B�������̂悤�ɑ��̒P���ƗZ�����Ă���͕̂ʂƂ��āB�B
�Ȃ̂ŁA���ЁA�����ɂȂ炸�A�J��}�X�^�[���Ă��������B
����Љ��̂́A�ȉ��I
����́A�m���̓p�^�[���Ȃ���Ȃ��A������P�����I���Ă������Ƃ��킩�����ɂȂ��Ă܂��B�����Ɏ���Ă݂Ă���������

 | ���i:1,676�~ |
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
-
no image
-
no image
-
no image
���̋L���ւ̃R�����g
�R�����g������
���̋L���ւ̃g���b�N�o�b�NURL
https://fanblogs.jp/tb/10949812
���u���O�I�[�i�[�����F�����g���b�N�o�b�N�̂ݕ\������܂��B
���̋L���ւ̃g���b�N�o�b�N