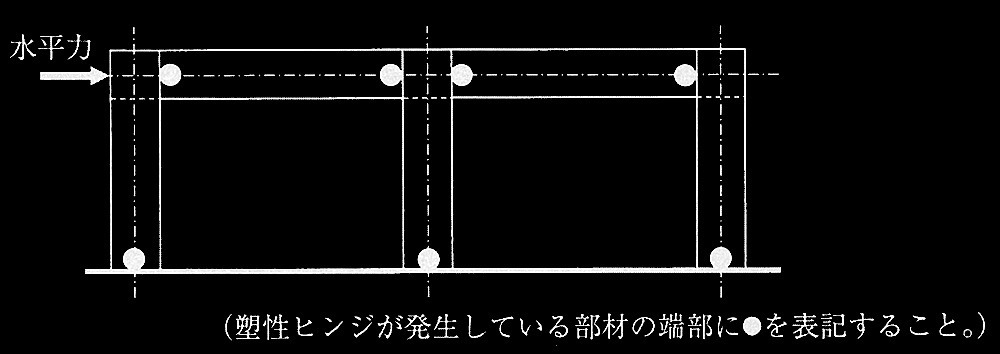
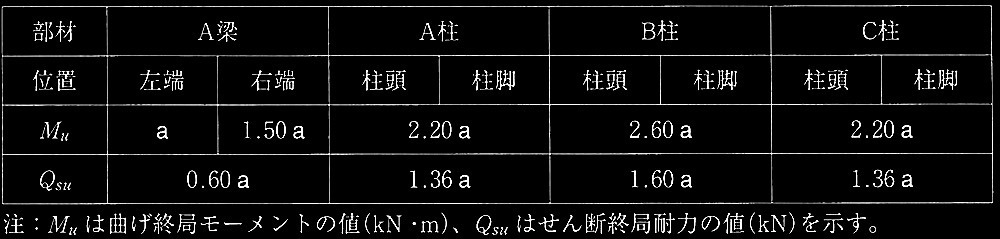
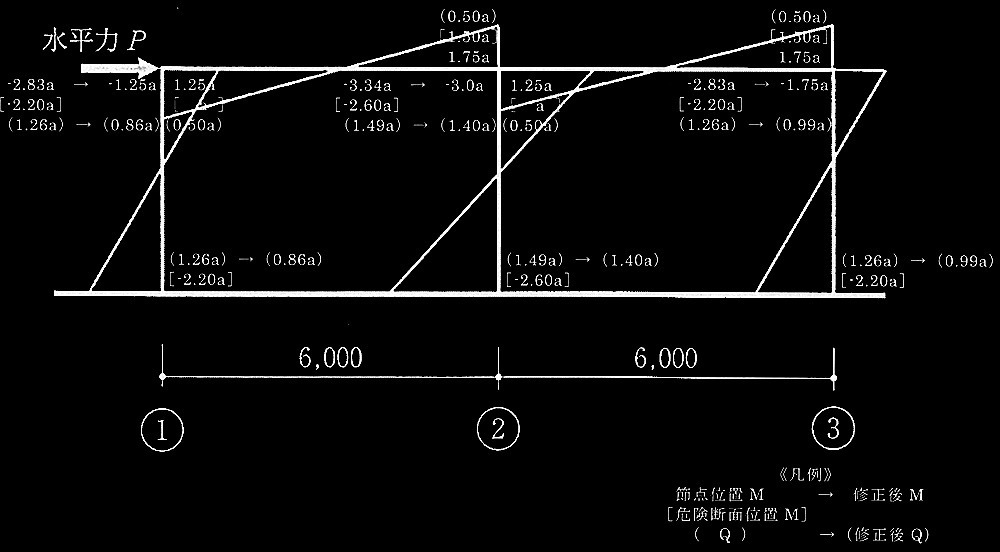
�C���l���i�@�K���m�F�j
�@�K���m�F
�i�I�𗝗R�L�q��4�����[���j
[ No. 1 ]
���z�\���v�̂���ׂ��p�Ɋւ��鎟�̋L�q�̂����A�ł��s�K���Ȃ��̂�I�сA�s�K���Ƃ��闝�R���q�ׂ��B
1. �\�����̈��S���Ɋւ��錩���ɂ��āA�g�D�̏�i�̔����ɂ��Ă��������Ɗ��������߁A�t�x���邱�ƂȂ���i�ɑ��Ď����̈ӌ����q�ׂ��B
2. �ۗL�����ϗ͌v�Z�ł́A�����H�ɑ�������n�k���ɑ��鉞���ό`�͗z�ɕ\������Ȃ����A�n�k��̑����x�ɑ傫���e�����邽�߁A�ʂ̕��@�ɂ���ĉ����ό`��]�������z��ɐ��������B
3. ��э\���v�Z�v���O�����ɂ����āA���ތ��肪���i�ƂȂ����Ƃ��Ă��A���炪�������Ă��Ȃ��v������ݒ肵�Ă͂Ȃ�Ȃ��B
4. �\�����̈��S���Ɋւ���V���Ȓm���ɂ��A���z��@�̍\���W�K��̉��������z����Ă��A�{�s�O�ł���ꍇ�ɂ́A���̉������e���\���v�ɔ��f������ׂ��ł͂Ȃ��B
����
�@�S
[ ��� ]
1. �L�q�̒ʂ�B
2. �L�q�̒ʂ�B
3. �L�q�̒ʂ�B
4. �����O�ł����Ă��V���Ȓm���������ꂽ�K��f�����邱�Ƃ͖]�܂����B������Ɋ����s�K�i�ɂȂ�\��������鎖�ɂ��Ȃ�B
[ No.2 ]
�\���W�K��̈ʒu�Â��ɂ����鎟�̋L�q�̂����A���z��@�y�ь��z�m�@��A�ł��s�K���Ȃ��̂�I�сA�s�K���Ƃ��闝�R���q�ׂ��B
1. ���z��@�́A�Œ����߂Ă���A���z�m�@�ł́A���z�m�͂�莿�̍������z���̎����ɓw�߂�K�v������Ƃ��Ă���B
2. ���זʐς� 600 m2�ł��錚�z��@��20���1����O���̓S�R���N���[�g���̊w�Z�ɂ��āA���e���͓x���v�Z�i���[�g2-1)���̗p�����ꍇ�A�\���v�[�����z�m�̎��i��ۗL���錚�z�厖�ɂ��m�F�R�����s����Ƃ��́A�\���v�Z�K��������y�э\���v�[�����z�m�̊֗^�͕s�v�ƂȂ�B
3. �����s�K�i���z���ɑ��đ��z���s���ꍇ�A���������ł́A���������̌��s��̓K�p���ɘa���邱�Ƃ��ł��邪�A���z���̏��L�ғ��ɂ́A�펞�K�@�ȏ�ԂɈێ����邽�߂̓w�͋`��������B
4. �\���v�͍s�킸�A�@�K���m�F�݂̂��s�����\���v�[�����z�m�́A���̊m�F�ɌW�錚�z���ɂ��āA���z��@��̐v�҂ɂ͊܂܂�Ȃ��B
����
�@�S
[ ��� ]
1.�L�q�̒ʂ�B�i���z�m�@��2����2)
2. �L�q�̒ʂ�B�i��@�{�s�ߑ�9����3)
3. �L�q�̒ʂ�B�i��@��8���j
4. �\���v���s���Ă��Ȃ��ꍇ�ł��@�K��������s�����ꍇ�͐v�҂Ɋ܂܂��B�i���z�m�@��20����2��3���j
[ No. 3 ]
���z��@�ɂ�����n�k�͂Ɋւ��鎟�̋L�q�̂����A�ł��s�K���Ȃ��̂�I�сA�s�K���Ƃ��闝�R���q�ׂ��B
1. �S�������z����ϐk�v�Z���[�g1-1�ɂ��v����ɓ�����A��b�̑ϐk�v�Z�ɂ��ď㕔�\���̑ϗ͊m�ۂɉe�����Ȃ������ɂ��ẮA�W������f�͌W����0.2�Ƃ����B
2. ������25m�̓S�R���N���[�g�����z���ɂ��āA���㕔������ˏo������p���̒n�k�͂���ʂȒ������͌����ɂ��Ȃ��Ōv�Z����ɓ�����A�]�|�A�ړ����ɂ���Q��h�~����[�u���u���邱�ƂƂ��A�����k�xk��1/2�Ɍ����Ēn�k�͂��Z�肵���B
3. �S�R���N���[�g�����z���̒n�k�͂ɂ��āA���z���̈ꎟ�ŗL�������ŗL�l��͂ŎZ�肷��ɓ�����A���ނ̂Ђъ���ɂ�鍄���ቺ���l������������p�����B
4. �n�k�͂̎Z��ɓ�����A���ʂȒ������͌����Ƃ��āA�n�Վ�ʂ̔���ɗp����n�Վ�������b��ʈʒu�̏펞�������茋�ʂ��狁�߂��B
����
�@�R
[ ��� ]
1. �L�q�̒ʂ�Ŗ��Ȃ��B �i�Z�p������P434, 15�`19�s�Q�Ɓj
2. �L�q�̒ʂ�B �i��12������1389���j
3. �n�k�͂��Z�肷��ۂ͍\���ϗ͏��v�ȕ����̏���������p������Ƃ��A�����ቺ�͍l�����Ă͂Ȃ�Ȃ��B �i��55����1793����3)
4. �L�q���e�Ŗ��Ȃ��B �i�Z�p������P. 305)
[ No. 4 ]
���z��@�ɂ�����d�y�ъO�͂Ɋւ��鎟�̋L�q�̂����A�ł��s�K���Ȃ��̂�I�сA�s�K���Ƃ��闝�R���q�ׂ��B
1. ������ȊO�̐����ϐጮ��15 cm�ȏ�ł�����ɂ�����S�������z���̋��e���͓x�v�Z�ɓ�����A�ܔ����̌��z��15�x�ȉ��ŁA���A�ŏ�[����ʼn��[�܂ł̐������e������10m�ȏ�̏ꍇ�A����Ɍ��z�����ɊY��������̂Ƃ��āA���������ɍ�p����ϐ�d�����葝���K�v������B
2. �\�����g�̕����͎Z��p�̑��x�����Z�肷�邽�߂̍���H�́A���z���̉������ύ����ŗ^�����A�v���錚�z���ɂƂ��Ĉ��̒l�ł��邪�A�O���ނ̕����ɑ���v�p�̕��ϑ��x�����̎Z��ɗp���鍂��H�́A�v����O���ނ̊e�X�̍����ɉ����ė^������B
3. �������������Ă��Ȃ������̒n���O�ǂɏ펞���������ɍ�p����v�p�y���́A�Î~�y�����̗p���邱�Ƃ��ł���B
4. �q�ɋƂ��c�ޑqჂɂ����鏰�̐ύډd�ɂ��āA�����ɉ����Čv�Z�������l��2,900 N/m2�ł����Ă��A3,900 N/m2���̗p���Ȃ���Ȃ�Ȃ��B
����
�@�Q
[ ��� ]
1. �L�q�̒ʂ�B �i��19��������594����3�z�j
2. �O���ނ̐v�p���ϑ��x�������߂�Ƃ��̍���H�͍\�����g�̕����͎Z��p�̑��x���Ɠ��l�ɍ����ƌ����̕��ϐ��@�ɂ��^�������̒l�ƂȂ�B�i��12������1458���j
3. �L�q�̒ʂ�B �i�Z�p������P.308)
4. �L�q�̒ʂ�B �i�{�s�ߑ�85���j
[ No. 5 ]
���z��@�ɂ�����S�����̑ϐk�v�Z�Ɋւ��鎟�̋L�q�̂����A�ł��s�K���Ȃ��̂�I�сA�s�K���Ƃ��闝�R���q�ׂ��B
1. ���e���͓x�v�Z�i���[�g1-2)�ɂ����āA�����͂S���������ۗL�ϗ͐ڍ��Ƃ���ꍇ�A�����Ƃ��ē��Y���������̗L���f�ʐς��Z�o�����~�����͂܂Őڍ������j�f���Ȃ����Ƃ��m�F����悢�B
2. ���e���͓x���v�Z�i���[�g2�j�ɂ����āA���[�����Ƌ������p�̍����\���ŋ����̐����͕��S����5/7�ȏ�̊K�ł́A���Y�K�̒n�����̕��މ��͂�1.5�{�Ɋ��葝���Đv���s���K�v������B
3. �ۗL�����ϗ͌v�Z�i���[�g3�j�ɂ����āA��Ԑ��`�p�`�|�ǒ�(BCP�ABCR�ށj��p�����ꍇ�A�������W������Ǖ����J�j�Y�����A���������U����S�̕��J�j�Y�������e�K���ʒu�Ŕ��f���A�Ǖ�����̏ꍇ�ɂ͓��Y���ʒu�̒��ϗ͂�ጸ���ĕۗL�����ϗ͂��Z�肷��K�v������B
4. �ۗL�����ϗ͌v�Z�i���[�g3�j�ɂ����āA�L�є\�͂��Ȃ��A���J�[�{���g���g�p���A�ۗL�ϗ͐ڍ��̏��������Ȃ��I�o���r��p����ꍇ�́A���Y�K�̒��y�ї��̕��ތQ�Ƃ��Ă̎�ʂ�D�ƂȂ�B
����
�@�P
[ ��� ]
1. �L���f�ʐςł͂Ȃ��S�f�ʐς��~������܂Ŕj�f���Ȃ����Ƃ����߂��A�Y�f�|�̏ꍇ�~�����͂�1.2�{�A�X�e�����X�|�̏ꍇ1.5�{�ȏ�K�v�B�i�Z�p������P.357)
2. �L�q�̒ʂ�B �i��55������1791���j
3. �L�q�̒ʂ�B �i��12��������594����4���O���j
4. �L�q�̒ʂ�B �i�Z�p������P. 636)
[ No. 6 ]
�S�R���N���[�g�����z���̑ϐk�v�Z���[�g1�ɂ����āA���L�̎�(1)�i����19�N���y��ʏȍ�����593���j��K�p����ہA���̋L�q�̂����A�ł��s�K���Ȃ��̂�I�сA�������𐳂��������B�Ȃ��A��(1)�̋L���͕���19�N���y��ʏȍ�����593���ɂ��B
�@��2.5��Aw + ��0.7��Ac �� ZWAi�@�@��(1)
1. �ˍ\���̓S�R���N���[�g�����J���ϗ͕ǂɂ����āA�ǔ̒f�ʐς� Aw�Ƃ��ĎZ�肷��B
2. �ˍ\���̓S�R���N���[�g�����J���ϗ͕ǂɂ����āA�����̒f�ʐς� Aw�Ƃ��ĎZ�肷��B
3. �ˍ\���̓S�R���N���[�g�����ŕǕt�����ɂ����āA����̏��������邻�ŕǂ̒f�ʐς� Aw�Ƃ��ĎZ�肷��B
4. �ˍ\�O�̓S�R���N���[�g���ǂɂ����āA����̏���������ǔ̒f�ʐς� Ac�Ƃ��ĎZ�肷��B
����
�@�Q
[ ��� ]
1. �L�q�̒ʂ�B
2. Aw��Ac
3. �L�q�̒ʂ�B
4. �L�q�̒ʂ�B
�i�Z�p������P. 382)
[ No. 7 ]
�؎��ޗ��y�і؎��\���Ɋւ��鎟�̋L�q�̂����A�ł��s�K���Ȃ��̂�I�сA�s�K���Ƃ��闝�R���q�ׂ��B
1. ��ɗ��ɗp����Ώ̈ٓ����\���W���ނ́A�O�w�Ɠ��w�̃��~�i�̋��x�͓����ł���B
2. ���z��@��20���1����l���̖ؑ����z���̑ϗ͕ǂ̕ΐS�̌����́A������u�l�����@�v�ōs���̂���ʓI�ł��邪�A�ΐS���̌v�Z���s���Ă��悢�B
3. �؍ނ̒������e���͓x�ɑ���Z�����e���͓x�̔�́A2/1.1 �ł���B
4. �؎��ޗ��̗��̂���v�Z�ɂ����āA�����d�ɑ���ό`����W���́A�\���W�K��ɂ��2�ƒ�߂��Ă���B
����
�P
[ ��� ]
1. �Ώ̈ٓ����\���W���ނ͓��w���O�w�̋��x���������邱�Ƃɂ��Ȃ��ɑ��Č��ʓI�ȑg�ݍ��킹�ɂ��Ă���B
2. �L�q�̒ʂ�B �i��12������1352���j
3. �L�q�̒ʂ�B�������e���͓x��1.1F/3�A�Z����2F/3�ł���B �i�{�s�ߑ�89���j
4. �L�q�̒ʂ�B �i��12������1459���j
[ No. 8 ]
�ϕ��v�Ɋւ��鎟�̋L�q�̂����A���z��@��A�ł��s�K���Ȃ��̂�I�сA�s�K���Ƃ��闝�R���q�ׂ��B
1. ���z���ɍ�p����v�p�̕����͂́A���y��ʑ�b����߂镗��Vo�A���ϕ����̍��������̕��z��\���W��Er�A�K�X�g�e���W��Gf�y�ѕ��͌W��Cf�Ȃǂ��l������Č��߂��Ă���B
2. �s�s�v������œs�s�����ɂ߂Ē������Ƃ��ē���s�������K���Œ�߂�n�\�ʑe�x�敪�W�̋��ł́A�n�\�t�߂Ō��z�����ɂ�鉚�ʂɂ�蕗�̗��ꂪ�傫���Ȃ邱�Ƃ���A���̒n�\�ʑe�x�敪�̏ꍇ�ɔ�ׂđ��x���͏������Ȃ�B
3. �����ʋy�ѕǖʂ̕��͌W�� Cf�́A���������̌��ʂɂ��Ȃ��ꍇ�A���^�E�J���^������̌��z���ł��A���z���̊O���W�� Cpe�i���O���瓖�Y�����𐂒��ɉ��������𐳁j��������W��Cpi�i�������瓖�Y�����𐂒��ɉ��������𐳁j�������ċ��߂�B
4. ���z��@�{�s�ߑ�87���2���ɋK�肷��E�̐��l�́A���ϕ����̍��������̕��z��\���W��Er�ɃK�X�g�e���W��Gf ���悶�ċ��߂�B
����
�@�S
[ ��� ]
1. �L�q�̒ʂ�B �i�{�s�ߑ�87���A��12������1454���j
2. �L�q�̒ʂ�B �i��12������1454���j
3. �L�q�̒ʂ�B�i��12������1454���j
4. Er�ł͂Ȃ��AEr��2���Gf���悶�ċ��߂�B�i��12������1454���j
[ No. 9 ]
�ۗL�����ϗ͌v�Z�Ɋւ��鎟�̋L�q�̂����A�ł��s�K���Ȃ��̂�I�сA�s�K���Ƃ��闝�R���q�ׂ��B
1. �K�v�ۗL�����ϗ͂̌v�Z�ɂ����ẮA�n�k�͂ɂ���Ċe�K�ɐ����鐅����Qud�̑傫�����A�e������1G�̐����͂Ƃ��Ă���B
2. �ÓI�d������͂ɂ��ۗL�����ϗ͂̌v�Z�́A�n�k���̉����ό`�����߂���̂ł͂Ȃ��A�ۗL�����ϗ͂ɒB���鎞�_�̕ό`�́A�n�k���̉����ό`�Ƃ͕K��������v���Ȃ��B
3. �\�������W��Ds�́A���z���̑Y���ό`�\�͂ɉ����āA���z���Ɋm�ۂ��ׂ����S���ł���B
4. �n�k���ɂ���Č��z���ɐ�����͂́A���̕��z�����X���X�ω����A�n�k�͂ɑ��錚�z���̋�������`�I�ɒ�`���邱�Ƃ͂ł��Ȃ����߁A�ۗL�����ϗ͂́A���炩���ߌ��߂�ꂽ���Ɋ�Â��v�Z���邱�ƂƂ��Ă���B
����
�@�R
[ ��� ]
1. �L�q�̒ʂ�B�i�Z�p������P. 341)
2. �L�q�̒ʂ�B�i�Z�p������P. 342)
3. Ds�͊e�K�̍\��������\�����̂Ƃ��āA���z���̍\���ϗ͏��v�ȍ\�����@�ɉ������������y�ъe�K���Ր��ɉ����Č��߂�ꂽ�K�v�ۗL�����σJ�̒ጸ�W���ł���B �i�Z�p������P.349)
4. �L�q�̒ʂ�B �i�Z�p������P. 344)
[ No. 10 ]
�S�R���N���[�g���ۗ̕L�����ϗ͌v�Z�Ɋւ��鎟�̋L�q�̂����A�ł��s�K���Ȃ��̂�I�сA�s�K���Ƃ��闝�R���q�ׂ��B
1. ���z�����Ր������҂��Đv����ꍇ�A���z���S�̂��ۗL�����ϗ͂ɒB����ȑO�ɂ���f�j��������Ȃ������ł͂Ȃ��A����`�ɒB����܂ł̒i�K�ł�����f�j���h�~����K�v������B
2. �A�w�ϗ͕ǂ̋r���������Ⓘ�ݍ��݂ɂ���]�n�̔j��`���ƂȂ�ꍇ�A�r���̕����Ⓘ�ݍ��݂��l�����đϗ͕ǂ̕��ގ�ʂ��߁ADs�̎Z����s���B
3. Ai ���z�Ɋ�Â��O�͕��z��p�����d������͂ɂ����Ds�Z�莞�ɕ���`���`�����Ă��Ȃ��K�̕���`�����߂���@�Ƃ��āA�]�ϗ͖@�i�d������͂ɂ�苁�܂镔�މ��͂ƕ��ޑϗ͂����Ƃɕ���`�����߂���@�j������B
4. �n�㕔���ɂ��ĕۗL�����ϗ͂��m�F����ꍇ�ł����Ă��A��b�̓v�͗v������Ă��Ȃ��B
����
�@�Q
[ ��� ]
1. �L�q�̒ʂ�B �i�Z�p������P. 348)
2. �A�w�ϐk�ǂ̗L���ɂ�����炸�����Ⓘ�ݍ��݂��������̂Ƃ���Ds���Z�肵�Ȃ���Ȃ�Ȃ��B �i�Z�p������P.402)
3. �L�q�̒ʂ�B�i�Z�p������P. 398)
4. �L�q�̒ʂ�B�i�Z�p������P. 434)