新規記事の投稿を行うことで、非表示にすることが可能です。
2024年08月09日
令和二年度修了考査 法適合確認 問題1
(1) 考査問題
令和2年度構造設計ー級建築士講習
修了考査(法適合確認)
問題1
一貫構造計算プログラムを用いたモデル化と構造計算に関する以下の設問に解答せよ。
[ No.1 ]
次に示す鉄筋コンクリート造耐力壁を含む架構の応力解析モデルに関する以下の①〜③の設問に解答せよ。
図1に示すような鉄筋コンクリート造耐力壁(EW)付きラーメン架構がある。1階の連スパン耐力壁を1層分の壁梁として上部構造の荷重を支持し、その荷重を全てA、E通りに設けた杭基礎に伝達する計画としている。この架構は、一貫構造計算プログラム内で、図2のようにモデル化される。この解析モデルを用いて、鉛直荷重時応力解析と長期の断面検定を実行する。その際、1FLと2FLの剛床仮定を解除する。
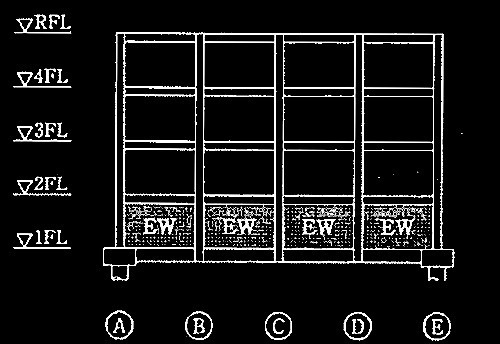
図1 耐力壁付きラーメン架構
↓ モデル化
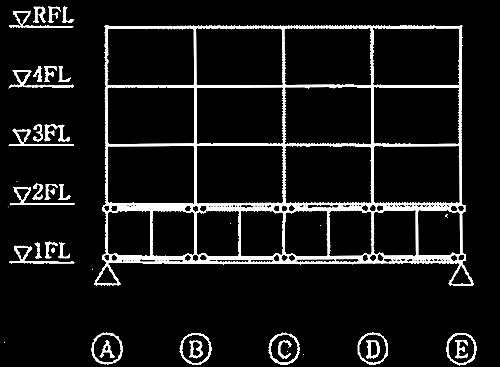
図2 応力解析モデル
ただし、耐力壁は図3に示す線材(壁エレメント置換モデル)としてモデル化され、同図中に示すとおり断面検定されるものとする。
壁 柱:耐力壁の壁板と等価な断面性能を有する柱材(せん断力に対して耐力壁として断面検定)
付帯柱:柱と同じ断面性能を有する両端ピンの柱材(軸力に対して断面検定)
付帯梁:梁の断面性能を100倍した梁材(断面検定の対象外)
剛な梁:断面性能が無限大の両端ピンの梁材(断面検定の対象外)
※ここに、断面性能とは、軸断面積A、せん断断面積As、断面二次モーメント I をさす。

↓ モデル化
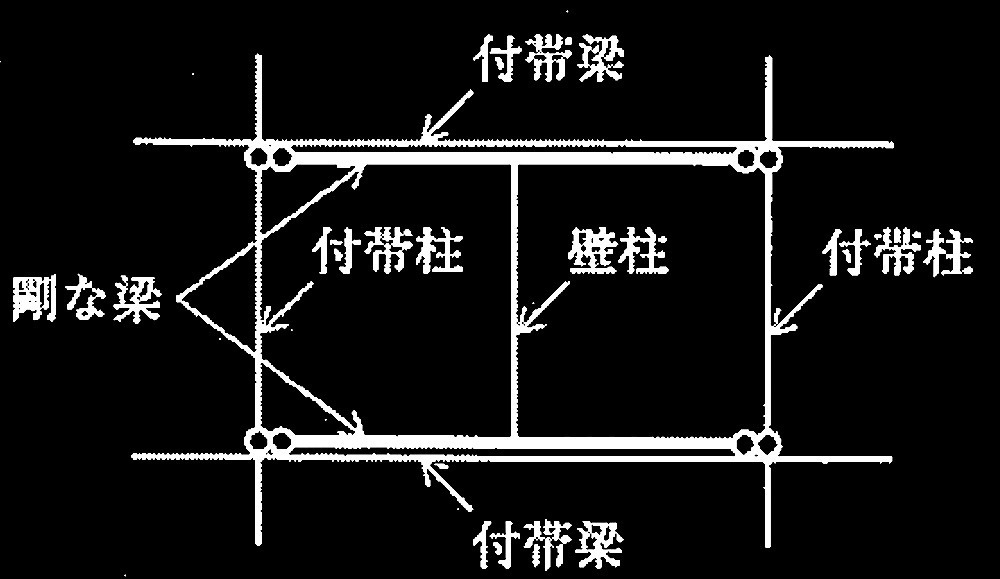
図3 耐力壁の壁エレメント置換モデル
① 壁エレメント置換モデルにおいて、付帯梁の剛性を増大(ここでは断面性能を100倍)させるのはなぜか、その理由を述べよ。
答え
[ 解答解説 ]
このモデル化では耐力壁の上下に想定している剛な梁および付帯柱の端部がピン接合となっているが、耐力壁の周囲に取りつく柱や梁などに生じる応力を適切に算定するため、耐震壁と付帯柱ならびに付帯梁による拘束条件を適切に評価するために付帯梁の曲げ剛性を増大させておく必要がある。
② 鉛直荷重時応力解析における、解析モデルの不都合点を一つ挙げ、その不都合点を解消する改善策を述べよ。
答え
[ 解答解説 ]
解析モデルは水平荷重による水平方向の曲げ・せん断力の算定の用のモデルとしては適切であるが、1階の耐震壁はA通りとE通りのみで支持され壁梁となっているため、鉛直荷重時の算定における鉛直方向の曲げ・せん断力に対する剛性については適切にモデル化されていない。
このような架構の場合は、耐力壁を板要素や鉛直方向のせん断剛性を同じとしたブレース置換によってモデル化して対応する。
もしくは、同様な考え方で適切にモデル化するためには、壁柱の代わりに壁梁、剛な梁の代わりに剛な柱、付帯梁ではなく付帯柱の剛性を増大させたモデル(現在のモデルを90゜回転させた形状)とする方法で対応する。
③ 長期の断面検定における、断面検定上の不都合点を一つ挙げ、その不都合点を解消する改善策を述べよ。
答え
[ 解答解説 ]
壁梁の長期応力による上端と下端の付帯梁に生じるはずの軸力が剛な梁に流れてしまうため軸力が生じない。
このような架構の場合は、耐力壁を板要素や鉛直方向のせん断剛性を同じとしたブレース置換によってモデル化して対応する。
もしくは、同様な考え方で適切にモデル化するためには、壁柱の代わりに壁梁、剛な梁の代わりに剛な柱、付帯梁ではなく付帯柱の剛性を増大させたモデル(現在のモデルを90゜回転させた形状)とする方法で対応する。
[ No.2 ]
図4に示すような鉄筋コンクリート造耐力壁(1〜3階、A-B間)付きラーメン架構がある。この架構の鉛直荷重時応力解析において、柱の軸変形を非考慮(軸剛性を無限大)とした。柱の軸変形を非考慮としたことについて、その課題(問題点・留意すべき事項等)を三つ簡潔に述べよ。
なお、基礎は十分な剛性を有しており、不同沈下は生じず、図のように柱脚はピン支持にモデル化できるものとする。
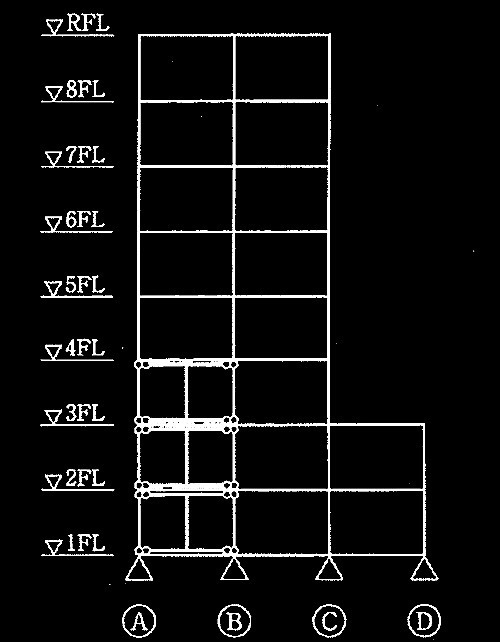
図4 耐力壁付きラーメン架構の応力解析モデル
※鉛直荷重時は柱の軸変形は考慮しない。
答え
[ 解答解説 ]
① 実際は1〜3階のA、B通りの柱の軸剛性が耐震壁の影響で大きく、他の通りよりも軸変形は小さいため、軸変形で梁に生じる部材角による梁応力、柱軸力ならびに基礎反力が正しく算定されない。
② 実際は高層部A-C間のB通り柱がA、C通り柱よりも大きく軸変形するため、軸変形で梁に生じる部材角による上層階の梁応力、柱軸力ならびに基礎反力が正しく算定されない。
③ 実際はD通り柱よりもC通り柱の1・2階柱の軸変形が大きいため、軸変形で梁に生じる部材角による2階、3階C-D間梁応力、柱軸力ならぴに基礎反力が正しく算定されない。
2024年08月08日
令和二年度修了考査 法適合確認 問題2
鉄筋コンクリート造建築物の耐震計算ルート3による設計に関する以下の設問に解答せよ。
[ No.1 ]
鉄筋コンクリート梁の種別の判定に関する以下の①〜③の設問に解答せよ。なお、対象とする梁(以下、「当該梁」という。)の諸元は図l、図2及び表1によるものとし、当該梁の種別判定では、接着する柱の種別は考慮しないものとする。
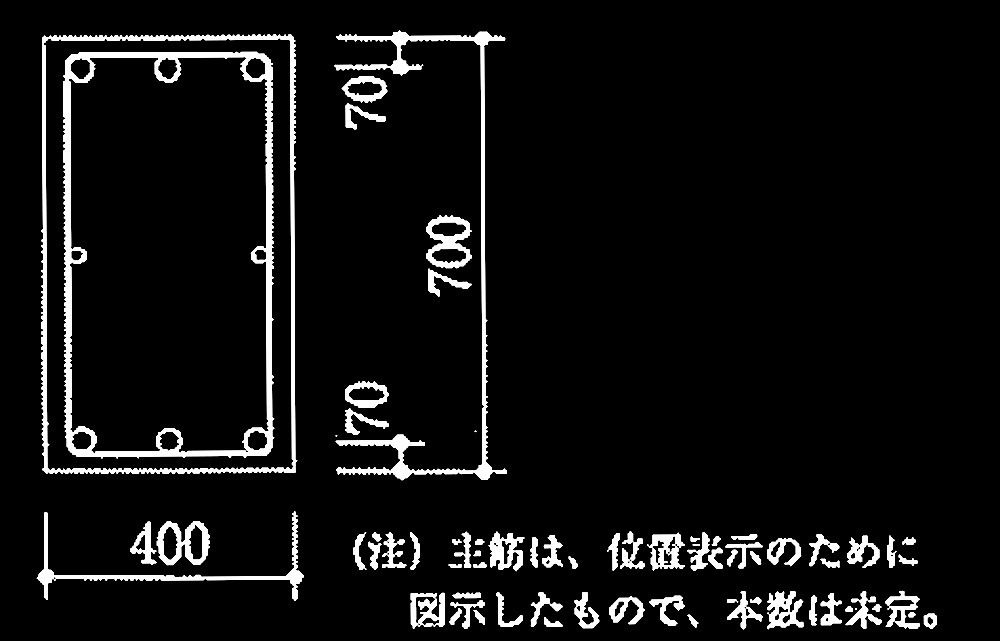
図1 梁断面 (単位:mm)
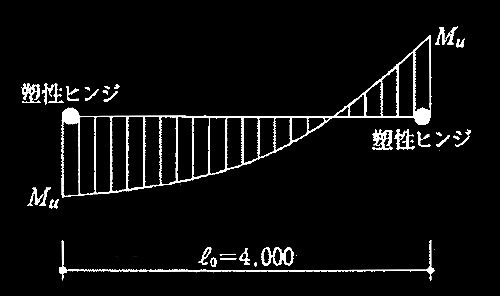
図2 梁の曲げ破壊時曲げモーメント分布 (単位:mm)
表1 当該梁の諸元(計算に用いる値)

【その他の諸条件】
(a) 梁の曲げ破壊時せん断力Qmuは、長期せん断力Qo、及び塑性ヒンジ発生時せん断力QMを用いて式(1)により算定する。ここで、QMは両端の曲げ終局モーメントMuの和を内法長さ ℓo で除した値とする。なお、床スラブの寄与は無視し、左端のMuと右端のMuは等しいものとする。
Qmu = Qo + QM 式(1)
ここに、QM = 2Mu/ℓo
(b) 梁の破壊モードは、梁のせん断終局耐力Qsuが式(2)を満足する場合には曲げ破壊(構造耐力上支障のある急激な耐力の低下のおそれがない。)とし、満足しない場合にはそれ以外の破壊(構造耐力上支障のある急激な耐力の低下のおそれがある。)とする。なお、付着の検討は別途行われているものとする。
Qsu ≧ Qo + 1.1QM 式(2)
① 当該梁の耐力等が次のように与えられる場合、当該梁の種別を昭和55年建設省告示第1792号に従って判定し、種別判定の根拠を簡潔に記述せよ。
【 耐力等の条件 】
長期せん断力 Qo = 0.020Fcbj
塑性ヒンジ発生時せん断力 QM = 0.035Fcbj
せん断終局耐力 Qsu = 0.062Fcbj
答え
[ 解答解説 ]
① Qo + 1.1QM = (0. 020+1.1 × 0.035) Fcbj = 0.0585 Fcbj (kN)
∴τu/Fc = 0.0585 ≦ 0.15
Qsu = 0. 062 Fcbj
∴ Qsu ≧ Qo + 1.1QM
以上よりこの梁の種別はFAとなる。
② 当該梁のせん断終局耐力Qsuが①の条件、Qsu = 0.062Fcbjとなるあばら筋の最小間隔を求めよ。梁のせん断終局耐力の算定式は式(3)によるものとする。

答え
[ 解答解説 ]
②「ただし、・・・」以下より式(3)は以下となる
Qsu = (0. 78 + 0. 85√(pw・σwy)) bj (kN)
そして、Qsu ≧ 0. 062 Fcbjより
(0.78+0.85√(pw・σwy) bj ≧ 0.062 Fcbj = 1.488 bj
0. 85√(pw・295) ≧ 0.708
pw ≧ (0.708 / 0.85)^ 2/295=0.00235
最小間隔を@とすると pw = 2 × 71/ b @≧0.00235
∴ @ 151.1 (mm)
③ 当該梁の種別がFDとなる引張主筋の最小本数を求めよ。その際、梁の曲げ終局モーメントMuは式(4)によるものとする。また、Qo及びQsuは①の[耐力等の条件 ] と同じ値とする。なお、主筋は一段筋とし、スラブ筋の寄与は無視する。

答え
[ 解答解説 ]
③ Qo, Qsuの値が①の耐力の条件と同じという事からFDとなるためには剪断破壊することが条件となる。
つまり、Qsu < Qo + 1.1QMとなることが条件となる。
QM > ((Qsu-Qo) /1.1) = ( 0.062 - 0.020 ) Fcb j /1.1=201966. 5N=202.0kN
QM=2Mu/ℓoなので、2Mu/ℓo> 202.0kN
∴ Mu > 202 × 4.0/2=404 kNm
上式と式(4)より
at = 404・106 / (0.9sσyd) =1899 mm2
∴ 4-D25 (2028 mm2)
●確認
Mu = 0.9・507・4・429・551/106=431
QM = 431・2/ 4.00=216
Qo = 0.020・24・400・551/103 = 106
Qo + 1.1QM = 106 + 1.1・216 = 344
Qsu = 0.062・24・400・551/103=328
[ No.2 ]
図3に示す鉄筋コンクリート造純ラーメン架構を対象に、非線形静的荷重増分解析(以下、「増分解析」という。)を実施して、保有水平耐力を計算した。図中の3箇所の1階柱(イ柱、ロ柱、ハ柱)について、以下の①〜③の設問に解答せよ。
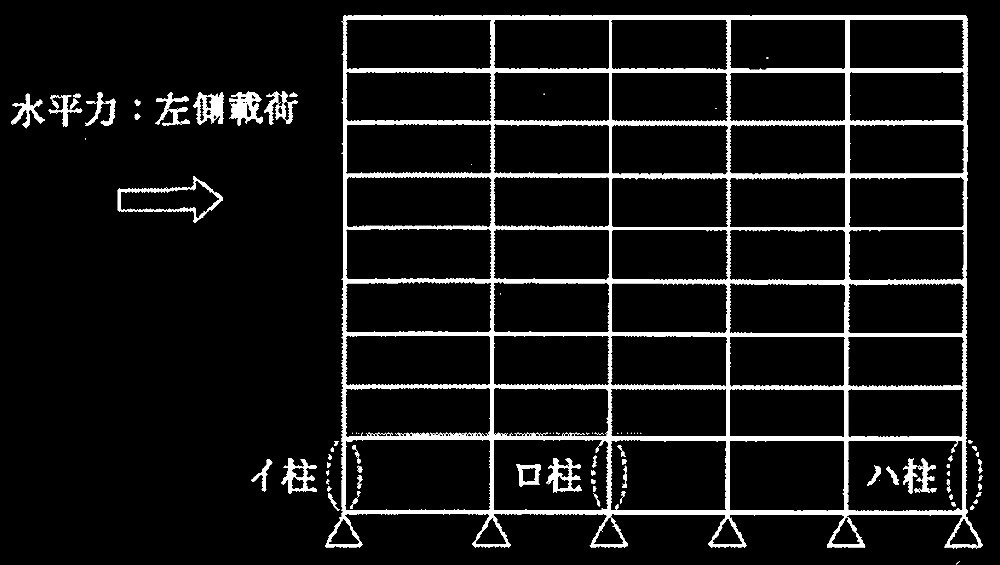
図3 解析対象の架構(純ラーメン構造)
【増分解析の条件及び解析結果】
(a) 増分解析の水平力は、一次設計用地震力の分布とし、図3に示すように左側から載荷した。
(b) 部材はせん断に対しては弾性とした。
(c) 増分解析では、柱の軸方向力Nと曲げ終局モーメントMuとの相関関係(N-Mu関係)を考慮した。図4に、3箇所の1階柱(A柱、B柱、C柱)の柱脚について、N-Mu関係は同一として増分解析の各ステップにおける軌跡をそれぞれ示す。なお、軸方向力は圧縮を正、引張を負とし、図中の括弧内の値は、該当ステップ時の軸方向力Nと柱脚曲げモーメントMaである。
(d) 増分解析終了時には、崩壊形を形成した。なお、 1階柱脚が曲げ破壊したが、 1階柱頭は曲げ破壊しなかった。
(e) 柱の破壊モードは、柱のせん断終局耐力Qsuが式(5)を満足する場合には曲げ破壊、満足しない場合にはせん断破壊とする。ここでは、 1階柱の柱脚塑性ヒンジ発生時せん断力QMは、式(6)による。その際、1階柱の曲げモーメントの反曲点高さは、図5に示すように 2/3 ho(ho:柱の内法高さ)とする。
Qsu ≧ 1.25QM 式(5)
QM =1.5Mu/ho 式(6)

図4 柱の軸方向力Nと曲げ終局モーメントMuとの相関関係
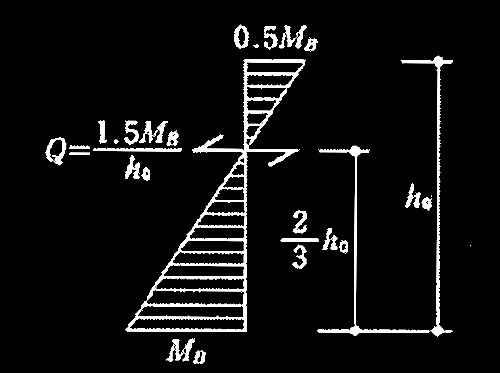
図5 1階柱の曲げモーメント分布
① 図4に示したA柱、B柱、C柱の軌跡は、それぞれ、図3のイ柱、口柱、ハ柱のどの柱に該当するかを推定し、その根拠を簡潔に記述せよ。
答え
[ 解答解説 ]
①
A柱:ハ柱 、軸力が次第に増加しているため
B柱:口柱 、軸力に変動がすくないため
C柱:イ柱 、軸力が次第に減少して最終的には引張になっているため
② 3箇所の1階柱(A柱、B柱、C柱)の破壊モードを曲げ破壊とするために必要なせん断終局耐力の下限値minQsuについて、下記の空欄に該当する数値を記入せよ。その際、柱のせん断終局耐力Qsuは軸方向力の変動に関わらず一定としてよい。
A柱のせん断終局耐力の下限値 minQsu = [ ] Mo/ho
B柱のせん断終局耐力の下限値 minQsu = [ ] Mo/ho
C柱のせん断終局耐力の下限値 minQsu = [ ] Mo/ho
答え
[ 解答解説 ]
②
技術基準解説書では、Ds算定時と保有水平耐力時に対する保証設計を行うこととしている。ここでは荷重増分解析中におけるM-N相関関係で最も不利な状況に対する検討とする。
A柱:1.5 × 1.00 × 1.25 = 1.88
B柱:1.5 × 0.80 × 1.25 = 1.50
C柱:1.5 × 0.60 × 1.25 = 1.13
③ 3箇所の1階柱(A柱、B柱、C柱)のうち、地震時に小さな変形において耐力低下が生じることが最も危惧されるのはどの柱か推定し、その根拠を簡潔に記述せよ。また、耐力低下を防止する対策として最も有効と考えられる方法を一つ簡潔に述べよ。
答え
[ 解答解説 ]
③
変形が小さい場合でも軸力比が大きい( Nu/No = 0.53 > 0.40)Aの柱が圧縮側コンクリートの圧壊によって耐力低下が生じやすい。
対策としては、帯筋を溶接型やスパイラル型にし、閉鎖型の副帯筋を用いてコアコンクリートを拘束する。また、帯筋や副帯筋を密にして主筋の座屈を防止する。
2024年08月07日
令和二年度修了考査 法適合確認 問題3
図1に示す2層の鉄骨ラーメン構造の建築物の崩壊メカニズムに関する以下の設問に解答せよ。なお、長期荷重による影響は無視するものとし、柱及び梁の部材断面、材種、基準強度F及び塑性断面係数Zpは、表1のとおりとする。
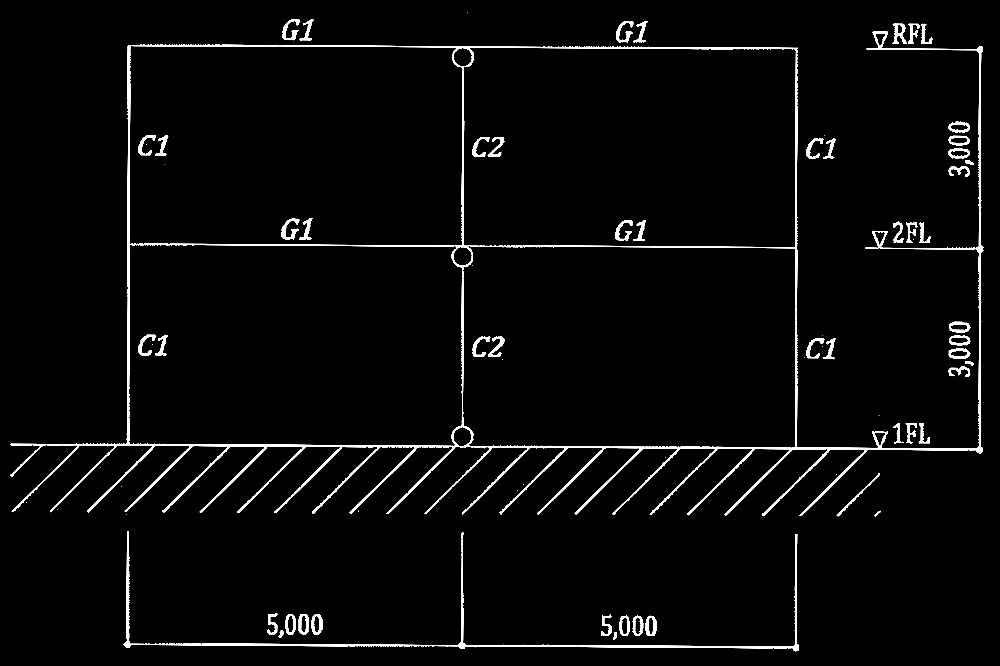
図1 骨組の解析モデル図(単位:mm、◯はピン接合を示す。)
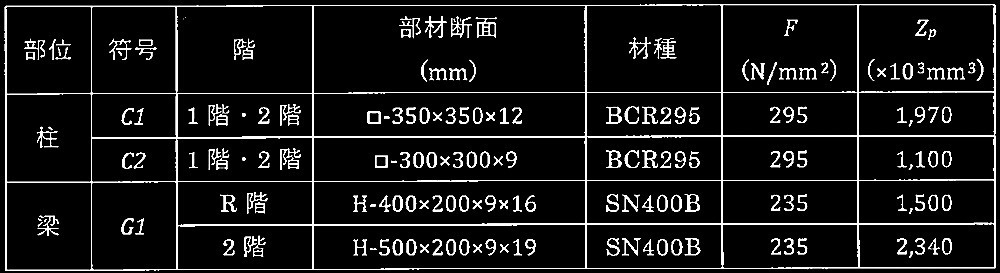
表1 柱及び梁の諸元
[ No.1 ]
表1に示した全ての柱及び梁の全塑性モーメントを算定せよ。なお、全塑性モーメント算定時の鋼材の降伏強度は基準強度Fの1.1倍とし、柱及び梁の全朔性モーメントは全断面有効と仮定し、柱の全塑性モーメントは軸力による低減はないものとする。解答は単位をkN・m とし、小数点以下を切上げて整数で示すこと。
答え
[ 解答解説 ]
・全塑性モーメントの算定
柱1,2FC1 cMp
= cF × cZp
= 295 × 1.1 × 1,970 × 103 / 10-6
= 640kN・m
柱1,2FC2cMp
= cF × cZp
= 295 × 1.1 × 1,100 × 103 / 10-6
= 357 kN・m
梁RG1 bMp
= bF × bZp
= 235 × 1.1 × 1,560 × 103 / 10-6
= 404 kN・m
梁2G1 bMp
= bF × bZp
= 235 × 1.1 × 2,340× 103 / 10-6
= 605 kN・m
[ No.2 ]
図2は、左側から水平力が作用したときの、崩壊メカニズム形成時の曲げモーメント図である。答案用紙のフレーム図に、全ての塑性ヒンジの発生位置を●で示せ。
塑性ヒンジが柱と梁のどちらに発生するかは、接合部に取り付く柱の全塑性モーメントの和と、梁の全塑性モーメントの和との比較により判断すること。ただし、梁は保有耐力接合がなされており、パネルゾーン及び部材の中間部に塑性ヒンジは発生しないものとする。
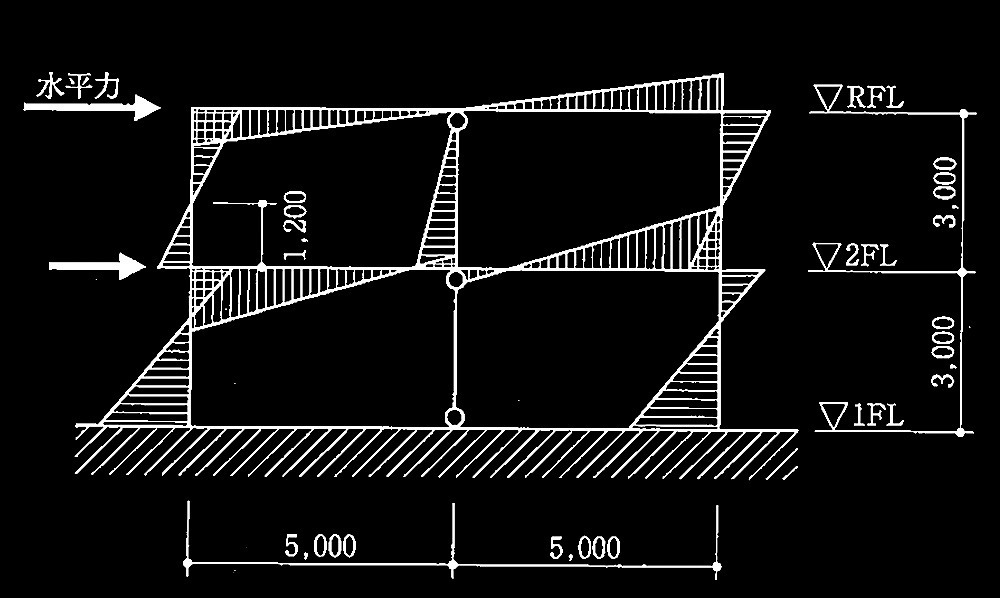
図2 崩壊メカニズム形成時の曲げモーメント図 (単位:mm)
答え
[ 解答解説 ]
・ヒンジの発生位置
RF 側柱 cMp(2FC1)
= 640 kN・m > bMp(RFG1)
= 404 kN・m → 梁端部
2F 側柱 cMp(2FC1) + cMp(1FC1)
= 639 kN・m + 639 kN・m
=1278 kN・m > bMp(2FG1)
= 605 kN・m → 梁端部
2F 中柱 cMp(2FC2)
= 357 kN・m < 2 × bMp(2FG1)
= 605 kN・m × 2
= 1210 kN・m → 柱脚部
崩壊メカニズム形成のため、1階C1柱脚にもヒンジが発生する。また、崩壊メカニズムとしては全体崩壊型、部分崩壊型のどちらかが想定されるが、図2の1階柱頭の曲げモーメントが柱脚に比べて小さいため、全体崩壊型とした。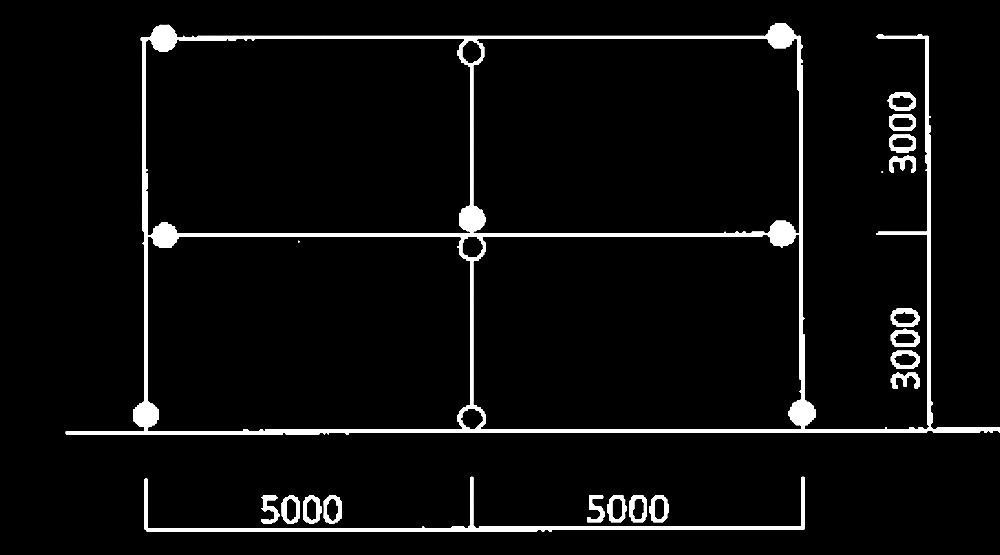
骨組のヒンジ発生位置を示す図(●がヒンジ発生位置)
[ No.3 ]
設問 [ No.2 ] の崩壊メカニズム形成時における右側の柱C1について、水平力によって生じる 2階の軸力2F(C1-R)Nu、及び1階の軸力1F(C1-R)Nuを求めよ。解答は圧縮を正、単位はkNとし、小数点以下を切上げて整数で示すこと。なお、塑性ヒンジの発生位置は節点位置としてよい。
答え
[ 解答解説 ]
問題[ No.1 ]で求めたヒンジ位置から軸力を算定する。
・2階軸力の算定
RFL梁端部にヒンジが発生することから、崩壊メカニズム形成時の柱付加軸力は下式となる。
2F(C1-R)Nu = 2 × bMp(RFG1)/梁スパン
=2 × 404kN・m/10m
= 81 kN
・1階軸力の算定
2階側柱は梁端部、中柱は2階柱脚にヒンジが発生することから、崩壊メカニズム形成時の柱付加軸力は下式となる。
1F(C1-L)NE = 2F(C1-R)Nu+ (bMp(2FG1) + cMp(2FC2) / 2) /梁スパン
= 81 kN+ (605 kN・m + 356 kN・m/ 2) / 5m
= 238 kN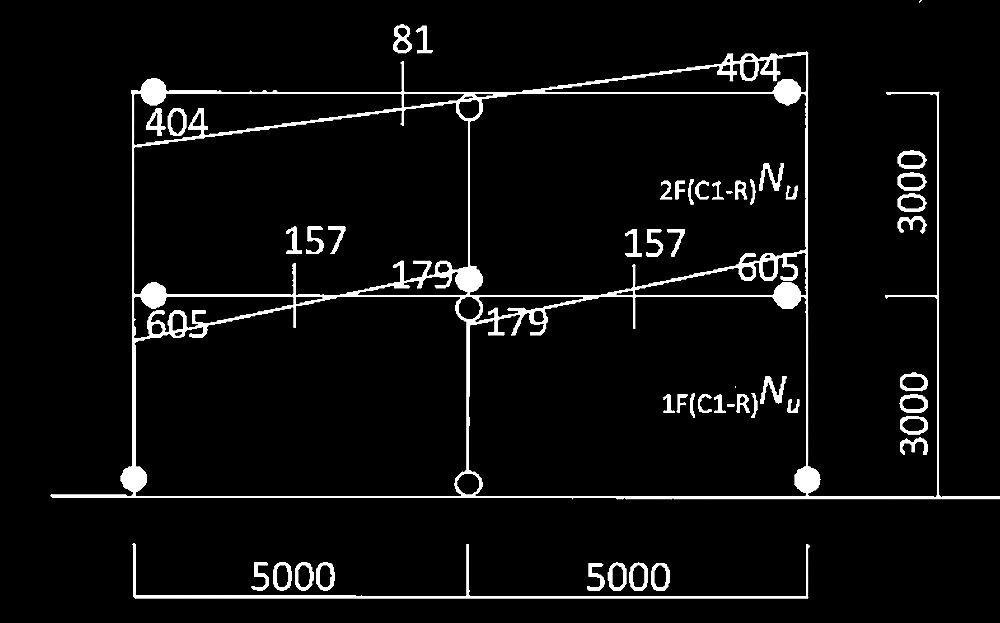
梁の曲げモーメント・せん断力図
[ No.4 ]
設問 [ No.2 ] の崩壊メカニズム形成時における2階の保有水平耐力2FQu、及び1階の保有水平耐力1FQu を求めよ。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。なお、 2階側柱の曲げモーメントの反曲点高さは、2FL+1,200mmとする。
答え
[ 解答解説 ]
問題 [ No.1 ]で求めたヒンジ位置から保有水平耐力を算定する。
・崩壊メカニズム時の曲げ応力及びせん断力分布は下図となる。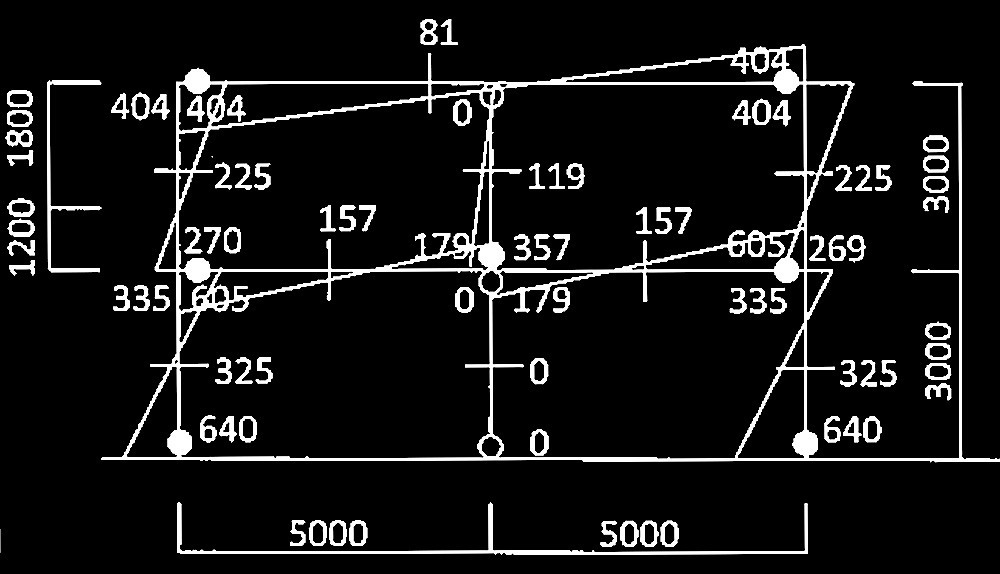
① 2階C1せん断力
404 kN /1.8m = 225kN
② 2階C1柱脚曲げモーメント
225 kN × 1.2m =270 kN
③ 2階C2せん断力
375 kN /3.0m = 119 kN
④ 1階柱頭曲げモーメント
つり合い条件より
605 kN - 270 kN =335 kN
⑤ 1階C1せん断力
(335kN + 640kN)/3m = 325 kN
・保有水平耐力は下式となる。
2FQu = 225 kN + 119 kN + 225 kN = 569 kN
1FQu = 325 kN + 0 kN + 325 kN = 650 kN
2024年08月06日
令和二年度修了考査 法適合確認 問題4
図1〜図3に示す2層2 × 2 スパンの鉄骨造骨組の設計に関する以下の設問に解答せよ。
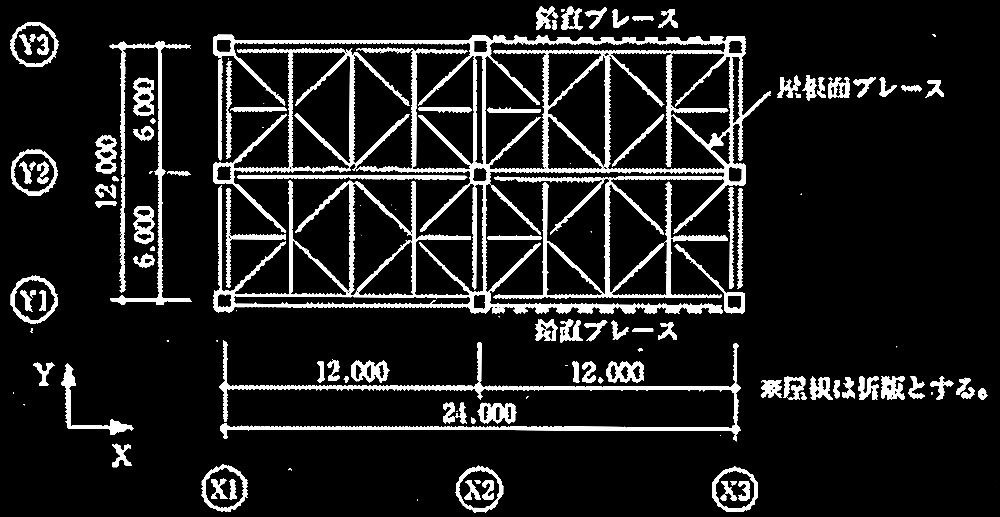
図1 R階伏図 (単位:mm)
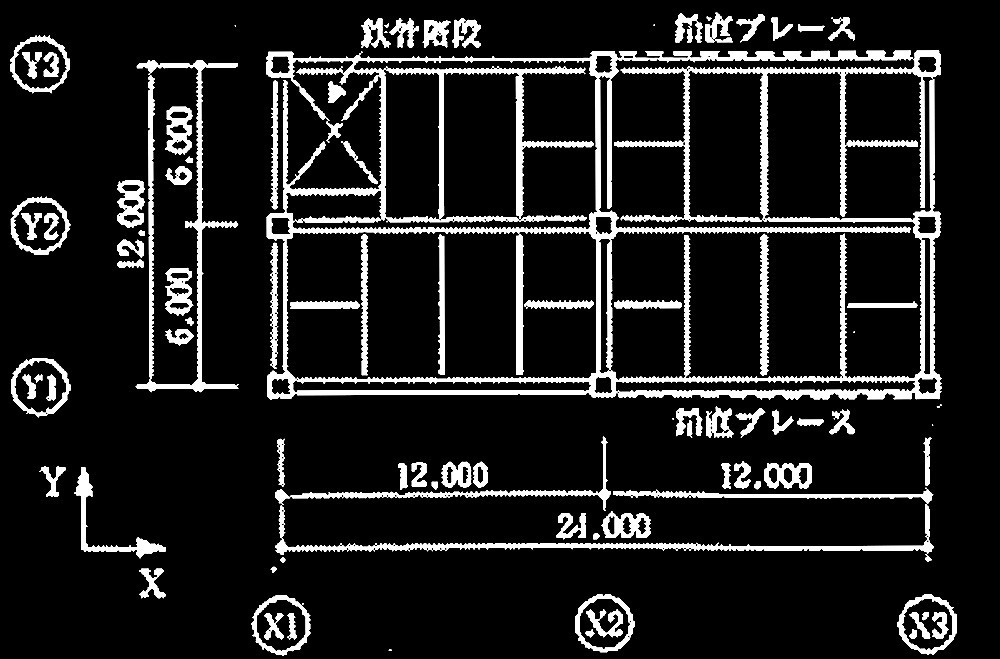
図2 2階伏図 (単位:mm)
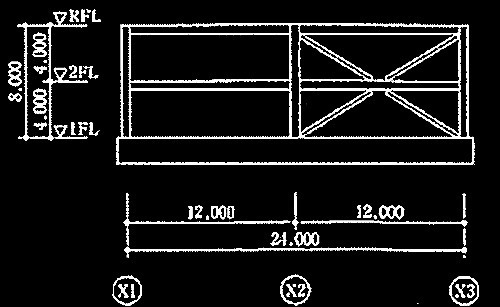
図3 Y1、Y3通り軸組図 (単位:mm)
[ No.1 ]
平成7 (1995)年兵庫県南部地震では、鉄骨造建築物の柱梁接合部における梁端部フランジの完全溶込み溶接部の脆性破壊が多く見られた。一般に、溶接接合部の脆性破壊は特定の条件が同時に満足される場合に限って生じると言われているが、その条件を3つ記述せよ。
答え
[ 解答解説 ]
(例)
・引張応力の存在
・切欠き部の欠損(応力・ひずみ集中源)の存在
・パス間温度管理不足などによる低靱性
[ No.2 ]
2階伏図において、X1通り、Y2〜Y3通り間の大梁には、鉄骨階段があるため、その間はスラブや小梁を設けることができない。このような場合の設計上の留意点及び対策を述べよ。
答え
[ 解答解説 ]
(例)
・解析モデルについて
留意点:他の大梁と異なりスラブがついていないことを、モデル化に適切に反映する。
対 策:モデル化において大梁の曲げ剛性割り増しを考慮しない。剛床仮定を解除する
・断面の検定について
留意点:階段部分に小梁が設けられないことに対して、横座屈長さを適切に評価する
対 策:横座屈長さを階段開口の長さで評価して、許容応力度の設定や保有耐力横補剛の検討を行う
留意点:X1-Y3通りの柱に対して大梁の軸力で地震力が伝達されることを考慮する
対 策:断面の検定において伝達される地震力に対する大梁の軸耐力の検討を行う
留意点:X1通りの外壁に加わる風圧力が大梁の弱軸方向に加わる可能性がある
対 策:大梁の弱軸方向の外力に対して、変形及び強度の検討を行う
外装の取り付け方次第では、ねじれ応力に対しての検討も行う
[ No.3 ]
2階伏図において、Y1通り、X1〜X2通り間の大梁は、小梁によって等間隔に横補剛されていると考えた場合、その補剛間隔が保有耐力横補剛の条件を満足するか否かを、下記の式(1)又は式(2)のいずれか片方の式を用いて検討せよ。どちらの式を用いるかは与条件により判断すること。

答え
[ 解答解説 ]
梁全長にわたって等間隔に横補剛されているため、式(1)を用いる。
・λy = 梁長さ / 弱軸まわりの断面2次半径
= 12,000mm / 70.4mm = 170.4
・nは横補剛(小梁)の箇所数 = 3
130 + 20 × n = 130 + 30 × 3 = 190
λy ≦ 130 + 20 × n より
保有耐力横補剛の条件を満足する。
[ No.4 ]
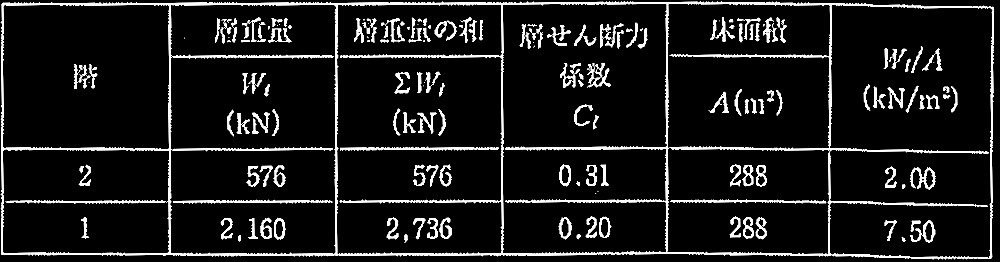
表1に一次設計用地震力算定用の層重量及び層せん断力係数を示す。X方向の地震力に対して、2階各フレームのせん断力の負担率を、Y1及びY3通りがそれぞれ40%、Y2通りが 20%とした場合、屋根面ブレース1本当たりの地震時設計上軸力を求めよ。なお、各通りの地震力算定には、単位床面積当たりの平均重量(Wi/A)を用い、屋根面ブレースは引張ブレースとし、各ブレースは均等に負担するものとする。
表1 一次設計用地震力算定用の層重量及び層せん断力係数
答え
[ 解答解説 ]
階全体の地震力及び、支配幅による各通りの地震力は下記となる。
・階全体の地震力:
ΣQ = ΣWi × Ci
= 576 kN × 0.31 = 178.6kN
・各通りの地震力:
Y1通り及びY3通り
支配面積 = 24m × 6m/2 =72m2
地震力 = Wi/A × 支配面積 × Ci
= 2.0 kN/m2 × 72 m2 × 0.31
= 44.6 kN
Y2通り
支配面積 = 24m × 6m = 144m2
地震力 = Wi/A × 支配面積 × Ci
= 2.0 kN/m2 × 144m2 × 0.31
= 89.3 kN
・各フレームの負担せん断力:
Y1通り及びY3通り
ΣQ の40% = 178.6 × 0.4 = 71.4kN
Y2通り
ΣQの20% = 178.6 × 0.2 =35.7 KN
・屋根面ブレースで伝達される地震力は、各通りの地震力と各フレームの負担せん断力の差で求める。
Y2通りから、Y1,Y3通りへ移行する地震力:
ΣQB = 71.4 kN – 44.6kN = 26.8 kN
屋根面ブレース1本あたりの負担地震力:
QB = ΣQB / ブレース台数
= 26.8kN / 4 = 6.7 kN
・屋根面ブレース1本当たりの地震時設計用軸力 NB
ブレース角度は 45° であるから、
NB = QB/cos45° =6.7kN / cos45° =9.5 kN
2024年08月05日
令和二年度修了考査 法適合確認 問題5
在来軸組工法による木造2階建て住宅の、地震力に対する耐力壁の設計に関する以下の設問に解答せよ。対象とする建築物の概要は以下に示すとおりで、図1に南側概略立面図を、図2に各階平面図を示す。図2中の太線部分は耐力壁を示しており、実線は壁の倍率 2.0、破線は壁の倍率1.0である。また、図2中に示したX、Yの矢印は地震時の水平力の加力方向を示している。
く建築物概要>
用 途 専用住宅
規 模 地上2階建て(小屋裏の利用なし)
延べ面積 116m2(1階:68m2, 2階:48m2)
構 造 在来軸組工法による木造
軒の高さ:6.1m、
最高高さ:7.3m、
階 高:1階及び2階ともに2.8m
仕上げ 屋根:瓦葺
外壁:サイデイングボード張り
建設地 多雪区域の指定のない区域(垂直積雪量:30cm)
地 盤 長期許容応力度:50kN/m2
その他 野地板及び床板:構造用合板直張り(いわゆる、剛床仕様)
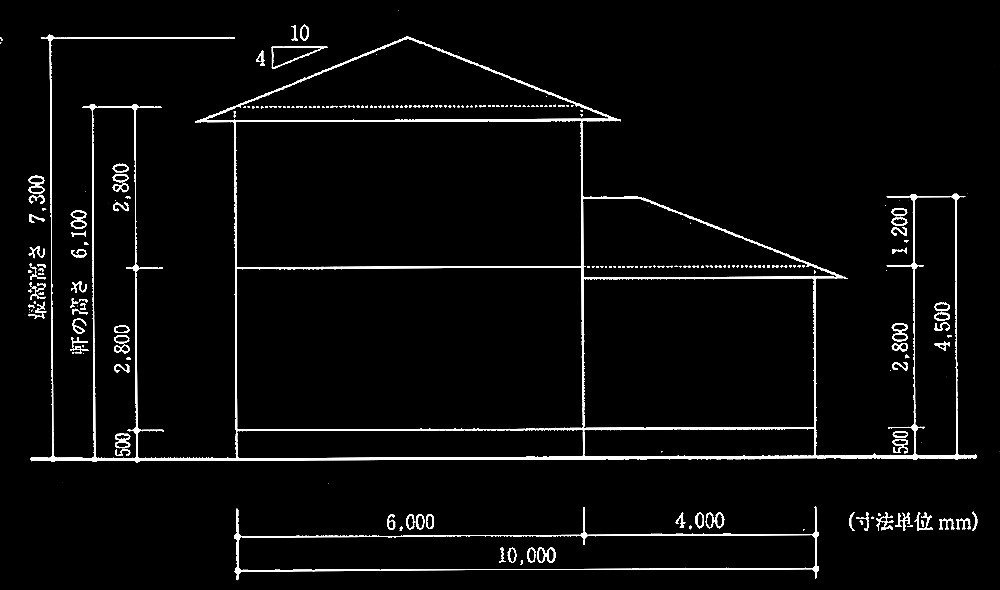
図1 南側概略立面図
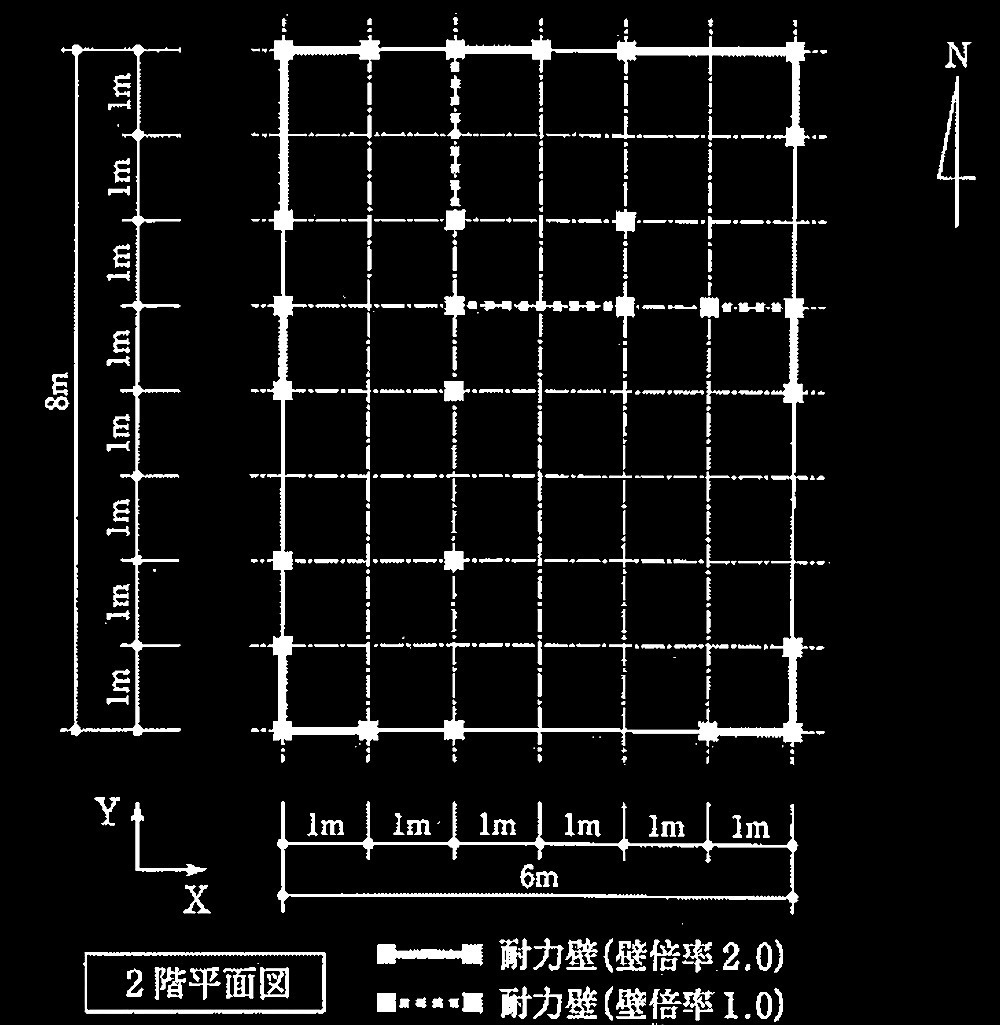

図2 各階平面図
表1 地震力用必要壁率 (m/m2)

[No.1]
この建築物の地震力に対する検討を、建築基準法施行令第46条の規定(いわゆる壁量計算)により行う場合について、以下の①及び②の設問に解答せよ。
①地震力に対する1階のX、Y方向の壁量が適合しているか否かを判定せよ。なお、地震力用必要壁率は、表1に示すとおりとする。
答え
[ 解答解説 ]
1階床面積
A= 10.0 × 5.0 + 6.0 × 3.0= 68.0m2
屋根仕上が瓦葺のため、地震力用必要壁率は重い屋根で算定する。
必要壁量 Lu= 68.0m2 × 0.33m/m2= 22.44m
X方向壁量
Lwx = (2.0m × 3枚 +1.0m × 6枚) × 2.0倍 + (2.0m + 1.0m) × 1.0倍
= 27.0m > 22.44m
∴ OK
Y方向壁量
Lwy = (2.0m × 2枚 + 1.0m × 4枚) × 2.0倍 + (2.0m × 2枚 + 1.0m × 3枚) × 1.0倍
=23.0m > 22.44m
∴ OK
以上より、地震力による壁量は1階は、X方向、Y方向共に適合している。
②四分割法により1階のX、Y方向の耐力壁配置が適合しているかを判定せよ。
答え
[ 解答解説 ]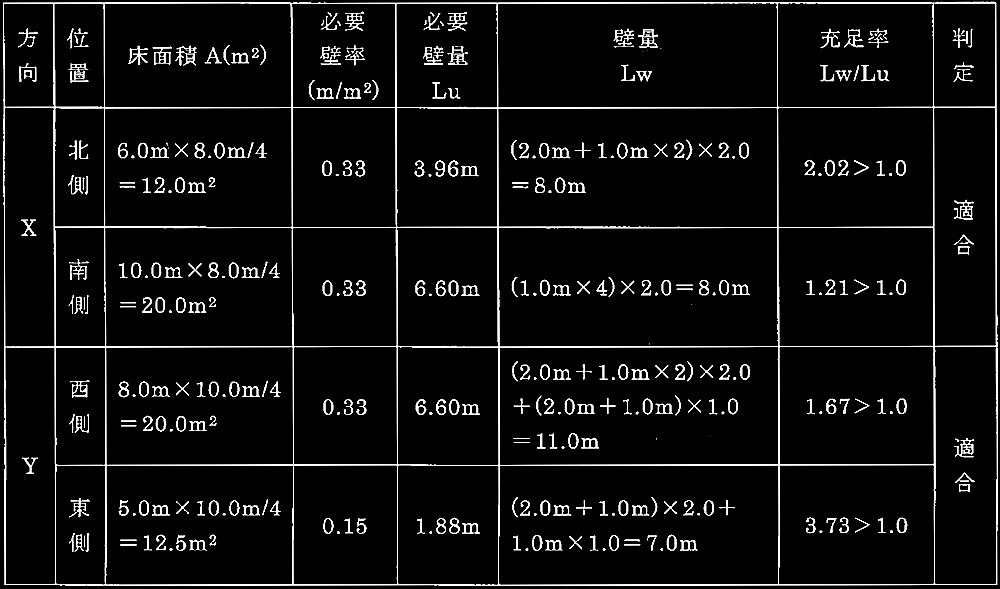
以上より、X・Y方向共に充足率が1.0を超えているため、壁率比に係わらず壁の配置は適合している。
[ No.2 ]
この建築物の地震力に対する耐力壁の検討を、許容応力度計算(構造計算)により行う場合について、以下の①及び②の設問に解答せよ。
①振動特性係数Rtを算出する際に用いる設計用1次固有周期Tを、昭和55年建設省告示 第1793号第2に示された式により求めよ。なお、建築物の高さは、軒の高さと最高高さの平均値を用いるものとする。
答え
[ 解答解説 ]
建築物の高さ
H= (7,300+ 6,100)/2= 6,700mm→6.70m
設計用一次固有周期
T= 6.70 × (0.02 + 0.01 × 1.0)=0.201秒
② 表2は地震力に対する安全性の検討を行ったものである。空欄(ア)〜(エ)に数値を記入し、判定欄の「適合」、「不適合」のいずれかを選べ。なお、表2は次の条件によるものとする。
1) 地震層せん断力係数 Ciは、Z =1.0、Rt =1.0、Co =0.2として算定している。
2) 壁倍率1.0の耐力壁の許容せん断耐力は、1.96 kN/mとして算定する。
3) ΣEQi は設計用せん断力を、ΣEPi は許容せん断耐力を表す。
表2 地震力に対する耐力壁の検討
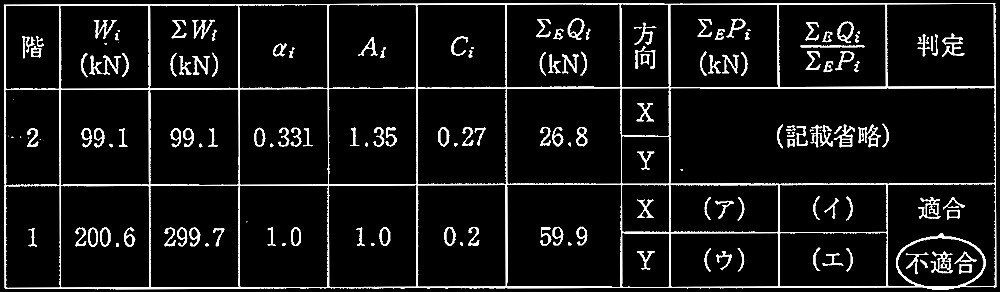
答え
[ 解答解説 ]
(ア) X方向 ΣEPi = 27.0m × 1.96kN/m = 52.92 kN
(イ) X方向 ΣEQi /ΣEPi = 59.9/52.92 = 1.13 > 1.00 NG
(ウ) Y方向 ΣEPi = 23.0m × 1.96kN/m = 45.08 kN
(エ) Y方向 ΣEQi /ΣEPi = 59.9/45.08 = 1.33 > 1.00 NG
以上より、X・Y方向共に地震力に対する耐力壁の検討は不適合である。
[ No.3 ]
木造建築物の地震力に対する検討を、設問 [ No.1 ]のような壁量計算による方法と、設問 [ No.2 ] のような許容応力度計算による方法で行った場合とでは、得られる判定結果(適合か不適合)が異なることもある。判定結果が異なる要因について述べ、木造建築物の設計に当たり、構造設計者としてどのように対応すべきかを簡潔に述べよ。
答え
[ 解答解説 ]
基準法の壁率が想定している建築物の重量より、最近の建築物重量は重い傾向があり、壁量計算が適合であっても詳細に建築物の重量を積算する許容応力度計算では不適合になる場合があるので、壁量計算による場合は余裕をもった壁量を確保する必要がある。