�}1�Ɏ���2�w2�X�p���̓S�������g�̐v�Ɋւ��鎟�̐ݖ�ɂ��ĉ���B�ϐk�v�Z���[�g��3�Ƃ��A���A����y�ы����̍ޗ������y�ђf�ʐ��\���̏����͕\1�`�\3�̂Ƃ���ł���B�Ȃ��A�����́A�\�ʓ��Ȃ����㎲���ƂȂ�悤�ɔz�u����A���ޒ������������Ɠ��f�ʂ̕��ނɂ������⍄����Ă�����̂Ƃ���B
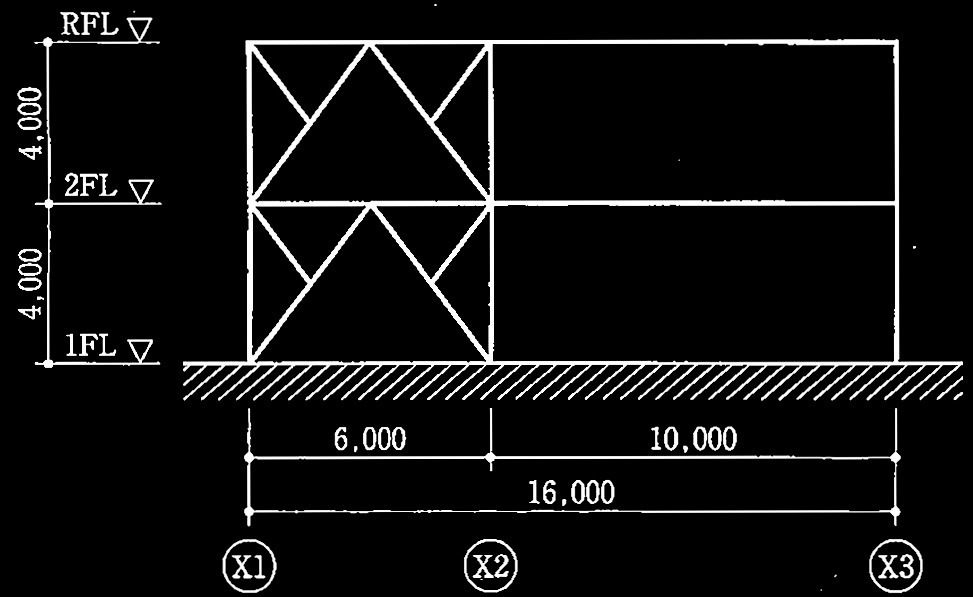
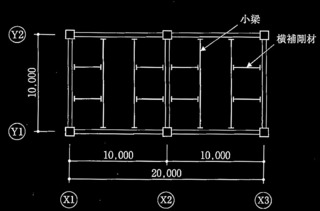
�}1 ���g�̃��f���}�i�P�ʁFmm)
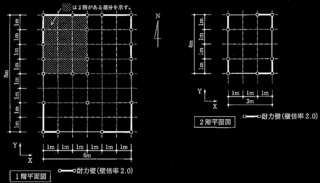
�\1 ���̏���

�\2 ����̏���

�\3 �����̏���


[ No.1 ]
�n�k���ɍ����x�����͂��J��Ԃ��钌���ڍ����̎d�����̗n�ڕ��ɂ́A�u�ԓI�ȋT��̓`�����Ɛ��j�������邽�߁A���x�̑����Ր����v�������B����[���ł̐Ɛ��j���h�~���A���肵���Y���ό`�\�͂��m�ۂ��邽�߁A�����ڍ����̎d�����̗n�ڂɂ��āA�u�\���v�v�y�сu�S������v���ꂼ��̒i�K�œ��ɗ��ӂ��ׂ��_���Ȍ��ɏq�ׂ�B
����
[ ��� ]
�u�\���v�v�ŗ��ӂ��ׂ��_�i��j
�E�،�����̌��ׂ̉���i���J�E�Ђ��ݏW�����̏����j
�@�m���X�J���b�v�H�@�̗̍p�Ȃ�
�E�����Ր��ޗ��̗̍p
�E���[���g���H�@�Ȃǂɂ��A�Y���q���W���n�ڈʒu�Ŕ������Ȃ��悤�ɂ���
�u�S������v�ŗ��ӂ��ׂ��_�i��j
�E�M�e�����Ȃǂ̕i�����m�ۂ��邽�߂̓��M�E�p�X�ԉ��x�̊Ǘ�
�E�V���[�g�r�[�h�̉����\�M�̕��p
[ No.2 ]
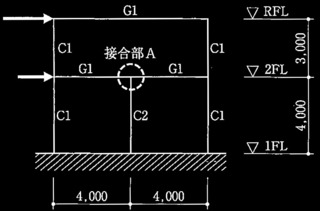
�}1�Ɏ����S�������g�����L(a)~(c)�̏����ɂ���ꍇ�ɂ��āA���̇@�y�чA�̐ݖ�ɉ���B
(a) �e���ނ̐ڍ����͕ۗL�����ϗ͐ڍ������Ă���B
(b) ���y�ё���̕�����́A�S�Ď��FA�����A����͑S�ĕۗL�ϗ͉��⍄����Ă���B
(c) ���r���͘I�o���r�ł��邪�A�ۗL�����ϗ͐ڍ������Ă���BDs�l�̊������͕K�v�Ȃ��B
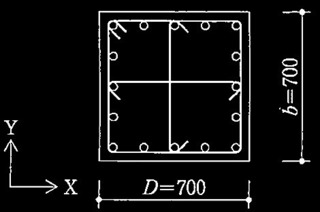
�@ 1�K�̋����ɂ��āA���ނƂ��Ă̎�ʂ����a55�N���ݏȍ�����1792���i�ȉ��A�u�����v�Ƃ����B�j�ɏ]���Ĕ��肵�A��ʔ���̍������Ȍ��ɋL�q����B
����
[ ��� ]
1�K�̋،������� L = ��(4,0002 + 3,0002) = 5,000 mm
�،����̍ג���
���� ���������@5,000 mm
��x = L / ix= 5,000 mm / 86.2 mm = 58.0
�㎲ �������� 5,000 mm/ 2 = 2,500 mm
��y= L / iy �� 2,500 mm/ 50.2 mm = 49.8
���ނ̍ג��� �� = max�i��x, ��y) = 58.0
⇨���a55�N���ݏȍ�����1792���E��3 �i�ŏI��������19�N5��18�����y��ʏȍ�����596���j���
(495 / �� F = 32.3) < ( ��= 58.0�j < (890/�� F =58.1)�ł��邩��A
���ގ��BB
�A 1�K�̕��ތQ�Ƃ��Ă̎�ʂ������ɏ]���Ĕ��肵�A�e�K�̍\�������W��Ds�l�����߂�B�܂��A���ތQ�Ƃ��Ă̎�ʔ���̍����y��Ds�l�̎Z�荪�����Ȍ��ɋL�q����B�Ȃ��ABu�� 0.4�Ƃ���B
����
[ ��� ]
���y�т͂�̕��ތQ�Ƃ��Ă̎�� A
���y�т͂�̑S���ނ�FA�ނł��邱�Ƃ���A��A =1.0 �� 0. 5
�� ���y�т͂�̕��ތQ�Ƃ��Ă̎�ʂ�A
�،����̕��ތQ�Ƃ��Ă̎�� B
�����̑S���ނ�BB��
�� �����̕��ތQ�Ƃ��Ă̎�ʂ�B
���y�т͂�̕��ތQ�Ƃ��Ă̎��A�A�����̕��ތQ�Ƃ��Ă̎��B�A0.3��(��u = 0.4) �� 0.7
⇨ ���a55�N���ݏȍ�����1792���E��3 �i�ŏI��������19�N5��18�����y��ʏȍ�����596���j���
Ds�l�@0.3
[ No.3 ]
�}2�̂悤��2�K��X2~X3�ʂ�̑���́A���������ɐ�������݂���v�����ł��邽�ߑS���ɂ킽��ϓ��Ԋu�ʼn��⍄�����邱�Ƃ��ł��Ȃ��B���̑Ή���Ƃ��āA�����[����1�ӏ������⍄����ꍇ�ɂ��āA���̇@�y�чA�̐ݖ�ɉ���B
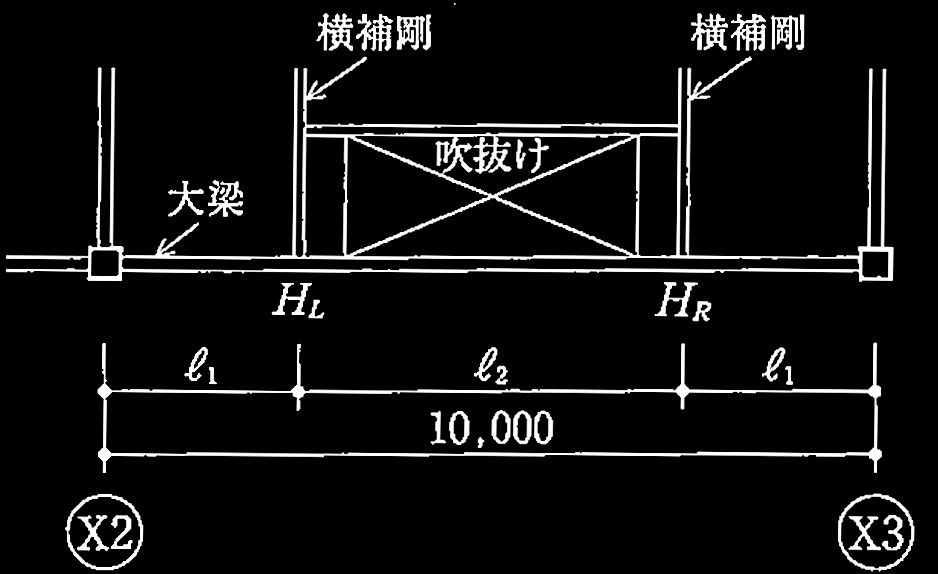
�}2 2�KX2�`X3�ʂ�̑�����͂̕��ʐ}�i�P�ʁFmm�j
�@ X2�ʂ肩�牡�⍄�ނ̈ʒu�܂ł̍ő勗�� ℓ1�������ɂ�苁�߂�B�Ȃ��A������ 400�j���[�g�����Y�f�|�̗��̉�������h�~���邽�߂ɁA���̒[���ɋ߂������ɉ��⍄��݂���Ƃ��̏������ł���B

�i�o�T�F2015�N�x�Ō��z���̍\���W�Z�p�������j
����
[ ��� ]
iy = 47.4 mm
Af = 200 × 22 = 4400 mm2
h = 500 mm
ℓb �� 250 × Af/h = 2200 mm
����
ℓb �� 65 × iy = 3081 mm
���t�F�C�X�ʒu�Ƀq���W���ł���Ƃ����ꍇ�A
ℓ1��2200 + 350/2 = 2375 mm
�A ���E�̉��⍄�ނ̈ʒu���@�ŋ��߂� ℓ1�Ō��肵�A���̈ʒu�����ꂼ��HL�AHR�Ƃ���Ƃ��AHL�`HR�Ԃɂ͉��⍄���s�v�ł��邱�Ƃ��v�Z�ɂ�莦���B�������A���⍄�����p�̋Ȃ����[�����g���z�ɂ́A���S�� ��= 1.2���悶�����̂�p������̂Ƃ��AMp�̎Z��ɗp����ޗ����x�́A����x F�l��1.1�{�Ƃ���B�܂��A�����d�͖���������̂Ƃ���B�Ȃ��AH�`�f�ʕ��ނ̒������e�Ȃ����͓x�͎��ɂ�苁�߂���̂Ƃ���B

�i����13�N���y��ʏȍ�����1024����1��O���n�\1(1)(��)�j
����
[ ��� ]
���[�~�����̗��[���̋Ȃ����[�����g
��Mp = 1.2 × Zp × 1.1F
=1.2 × (2,600 × 103)mm3 × 1.1 × 235N/mm2 × 10-6 = 8.07 × 108N�Emm = 807kN�Em
���t�F�C�X�ʒu�ŗ��[����Mp�ƂȂ�Ƃ��̗��[������ℓ1�̈ʒu�ł̋Ȃ����[�����g
�����@�X�p�� 10,000mm �|350mm = 9,650 mm
Mℓ1 = 807 kN�Em × (9,650 mm �| 2,200 mm × 2) / 9,650 mm= 439 kN�Em
HL�`HR�Ԃ̒[���Ȃ����[�����g����q��M1 = M2�ƂȂ�Ƃ���HL�`HR�Ԃ̒Z�����e�Ȃ����[�����gMs
M1 = M2 = 439 kN�Em
�Ȃ����[�����g���z�����ȗ��Ȃ̂�M2/M1= 1.0
�� C = 1.75 + 1.05 × 1.0 + 0.3 × 1.02 = 3.10
�� C= 2.3
�� = 1500/�� (235/1.5) = 120
ℓb = 10,000 mm – 2,375mm × 2
�@= 5,250mm (HL�`HR�Ԃ̒����j
ib= 54.0mm
Af= 200mm × 22 mm = 4,400 mm2
h= 500 mm
fb1 = 235 x (2/3 – 4/15 × (5250 / 54.0)2 / (2.3 × 1202)) = 139 N/mm2
fb2��89000/(5250 x 500 / 4400) = 149 N/mm2
fb = max(fb1,fb2) = fb2��149 N/mm2
����ĒZ�����e�Ȃ����[�����gMs�́A
Ms= Zx × 1.5 × fb
= (2,330 × 103) mm3 × 1.5 × 149 N/mm2 = 4.89 × 108 N�Emm = 521 kN�Em
Mℓ1(439kN�Em) < Ms(521 kN�Em)�ƂȂ�A���̗��[����Mp�ɒB����Ƃ��̗��[������ℓ1�̈ʒu�ł̋Ȃ����[�����gMℓ1�́A�Z�����e�Ȃ����[�����gMs��菬�����B
HL~HR�Ԃɂ͉��⍄�͕s�v�ł���B