2024�N09��09��
�ߘa�l�N�x�C���l�� �\���v�i�L�q���j���R
���R
�ꏊ�ł��S�R���N���[�g�g��Y�̐v�Ɋւ��鎟�� [ No.1 ]�`[ No.3 ] �̐ݖ�ɉ���B�n�Ս\���ƍY�̐��@���̏����͐}1�̂Ƃ���ł���B
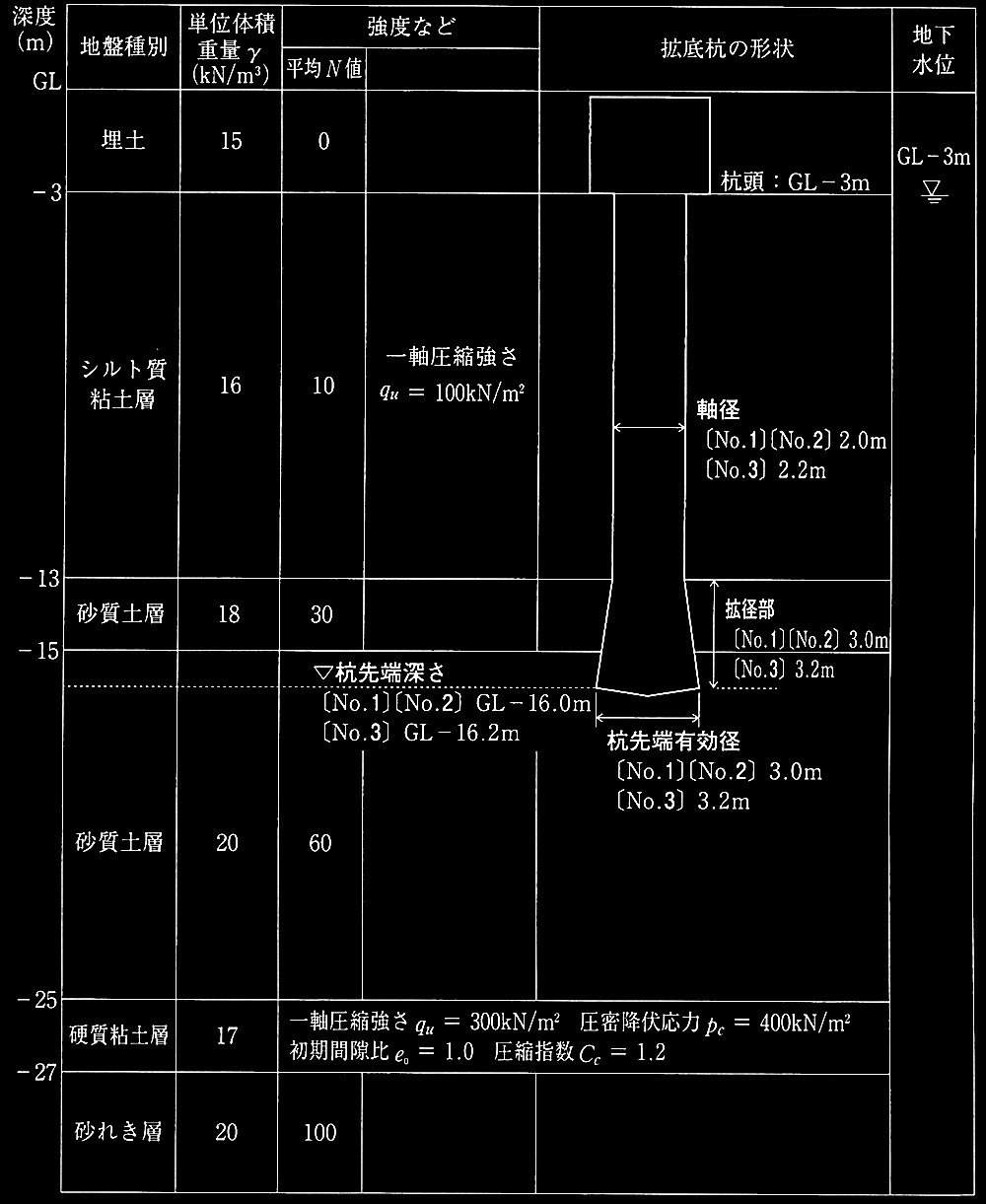
�}1 �n�w�\���ƍY�̏���
[ No.1 ]
�Y����GL–3m�A�Y��[�[����GL–16 m�Ƃ����ꏊ�ł��R���N���[�g�g��Y�i���a�F2m�A�Y��[�L���a�F3m�j���Ɍ���[��R�� Rp�y���Ɍ����ʒ�R��Rf�����L�̂��ꂼ��̎��ɂ��Z�肵�A�����̌��ʂ�p���Ď�(1)�ɂ���������e�x���� R��L���Z�肹��B
�������AGL–25�`27m�̍d���S�y�w�͈ꎲ���k�������\���ɂ���A�Y�̎x���͂͂��̏�̍��w�Ō��܂���̂Ƃ���B�܂��A�g�a���̎��ʒ�R�͍͂l�����Ȃ����̂Ƃ���B

����
[ ��� ]
�v�Z�͗L������3���ōs���A���ʂ��L������3���Ŏ����B�����́A�l�̌ܓ��Ƃ���B
R��L = 1/3 × ( Rp + Rf )�@�@��(1)
�Y��[�L���a = 3m���AGL�|13m�`GL�|19m�Ԃ̕���N�l�́A
N = (30 + 30 + 60 + 60 + 60 + 60)/6 = 50
�Ɍ���[��R��Rp�́A
Rp = 100 × N•Ap
�@ =100•50•(3.0/2)2×��
�@ = 35,325��35,300 (kN)
Rfs = 3.3Ns•Ls•��
�g�ꕔ�̎��ʒ�R�͍͂l�����Ȃ����߁A
Ls = 0 �� Rfs = 0 (kN)
Rfc = 0.5qu•Lc•��
�@ = 0.5•100•10•2.0��
�@ = 3,140 �� 3,140 (kN)
�Ɍ���[��R��Rf�́A
Rf =Rfs + Rfc = 0 + 3,140 = 3,140 (kN)
���������āA�������e�x����R��L�́A
R��L =1/3 × (35,300 + 3,140)
�@�@= 12,813��12,800 (kN)
[ No.2 ]
�������͂��}1�� [ No.1 ]�̍Y���ɍ�p����Ƃ��AGL–25�`27m�̈ʒu�̍d���S�y�w�̈��������̉\�����ȉ��̎菇�Ō�������B
�@ ���n�Ղ̍d���S�y�w��ʈʒu�iGL–25 m)�̉����L�����̓�o�f�����߂�B�������A�n�����ʈȐ[�̓y�̒P�ʑ̐Ϗd�ʂ͐����P�ʑ̐Ϗd�ʂ�p���A���̒P�ʑ̐Ϗd�ʂ�10 kN/m3�Ƃ���B
����
[ ��� ]
�����L�����̓�'o�́A�n�\�ʁiGL�}0m�j����d���S�y�w��ʈʒu�iGL�|25m�j�̊e�n�Ղ̒P�ʑ̐Ϗd�ʃ� × �w�� t �̘a�ł���B
�����ŁA�n�����ʈȐ[�ƂȂ�V���g���S�y�w�A�����y�w�̒P�ʑ̐Ϗd�ʂ͐����P�ʑ̐Ϗd�ʂ�p����B
�Ёfo = 15 × 3 �@�i���y�j
�@�@+ (16 �| 10) × (13 �| 3) �@�V���g���S�y�w(GL�|3�`�|13m)
�@�@+ (18 �| 10) × (15 �| 13) �@�����y�w(GL�|13�`�|15m)
�@�@+ (20 �| 10) × (25 �| 15) �@�����y�w(GL�|15�`�|25m)�@�@�@
�@= 221 (kN/m2)
�A �Y��[�ʂɒ�������12,000 kN�������z�ɍ�p���A����ɐ[��������1:2�i���F�����j�ʼnd�����U�����Ɖ��肵���ꍇ�̍d���S�y�w��ʈʒu�̑������̓�p�����߂�B
����
[ ��� ]
�Y��[�`�d���S�y�w��ʂ܂ł̐[��d = 25�|16 = 9m
�d�̕��U���l�������Ƃ��A�d���S�m�w��ʂɂ����Ē������͂���p����ʐ�AP'�́A
A�fp = {( 9/2 + 3 + 9/2)/2}2•��
�@ = 113.04 ��113 (m2)
�������̓�p��12,000/113 = 106.2��106 (kN/m2)
�B �@�y�чA���A�Y�̒������͂��l�������d���S�y�w��ʈʒu�̉����L�����̓Ёf�����߂�B
����
[ ��� ]
�Ёf = �Ёfo + ��p
�@= 221+106 = 327 (kN/m2)
�C �Ёe�ƍd���S�y�w�̈����~������ pc���r���A���������̉\���̗L���肵�A���̍������Ȍ��ɋL�q����B
����
[ ��� ]
�Ёf = 327 < pc= 400 (kN/m2)���A���������͐����Ȃ��B
���R�F�Y�̒������͂��l�������d���S�y�w��ʈʒu�ɂ����鉔���L�����͈͂����~�����͈ȉ��ł��邽�߁B
[ No.3 ]
�Y���� [ No.1 ]�Ɠ���GL–3m�̂܂܂Ƃ��A�Y��[�[����GL–16.2m�A���a��2.2m�A�Y��[�L���adp��3.2m�ɂ��ꂼ��[ No.1 ]����ύX�������ʁA�Ɍ���[��R��Rp��40,600 kN�A�Ɍ����ʒ�R��Rf ��3,450 kN�ƎZ�肳�ꂽ�B
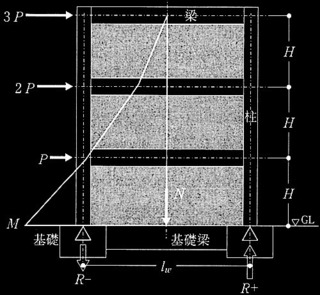
���̍Y���ɒ�������14,000 kN����p����Ƃ��̍Y�̒����ʓ��Ɋւ���ݖ�@�`�B�ɉ���B�������A�Y�̂͏\���Ɏ��������傫���A���̈��k�ʂ����邱�Ƃ��ł��A���Y���ʒ�R�͂ƒ����ʂ̊W�͐}2�Ɏ����悤�ȃo�C���j�A�ɁA�Y��[�dPb�ƍY��[������Sb�̊W�͐}3�Ɏ����Ȑ��A��(2)�ŕ\�������̂Ƃ���B
�܂��A�S�y�w�̎��ʒ�R�͂̐܂�_Sf��6mm�Ɖ��肷��B

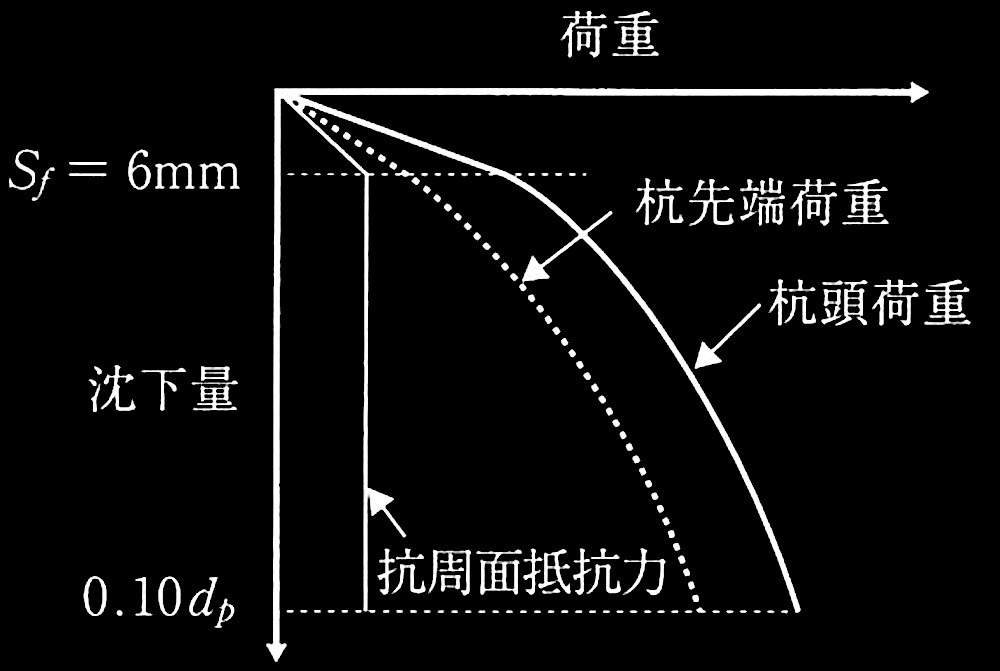
�}2 �d–�����ʊW�i�͎��}�j
�@�@
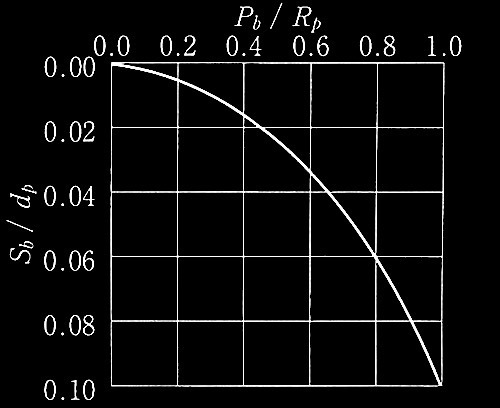
�@�@�}3 �Y��[�d–�Y��[�����ʊW
�@�@(a = 0.23�An = 2.7)
�@ �Y��[�����ʂ�Sf(= 6mm)���A�Y���ʒ�R�͂��Ɍ����ʒ�R��Rf�ɒB���Ă���Ɖ��肵���Ƃ��̍Y��[�dPb�����߂�B
����
[ ��� ]
�������� = �Y���ʒ�R�� �{ �Y��[�d
�ł���B
�����ŁA�Y���ʒ�R�͂��Ɍ����ʒ�R��Rr�ɒB���Ă��邱�Ƃ���A�������� NL = Rf + Pb
���������āA
�Y��[�d Pb = 14,000 �| 3,450
�@�@�@�@�@�@ = 10,550��10,600 (kN)
�A ��(2)��dp, Pb. Rp, a, n�������āA�Y��[������Sb�����߂�B
����
[ ��� ]
(Sb/dp)/0.1 = ��Pb/Rp +(1�[��)(Pb/Rp)n�@��(2)
dp = 3.2 (m), Pb = 10,550 (kN), Rp = 40,600 (kN), ��= 0.23, n = 2.7��������Sb�����߂�ƁA
Sb = 0.1•3.2 (0.23 × 10,600/40,600 + (1- 0.23)(10,600/40,600)2.7) = 0.0258 (m)
����āA
Sb = 25.8 (mm)
�B �A�ŋ��߂��Y��[������Sb��Sf(= 6mm)�Ƃ��r���āA�@�ōY���ʒ�R�͂��Ɍ����ʒ�R��Rf�ɒB���Ă���Ɖ��肵�����Ƃ��A�Ó��ł��邩�ۂ��f���A���̍������Ȍ��ɋL�q����B
����
[ ��� ]
Sb = 25.8 > Sf =6.0 (mm)���A
�@�ōY���ʒ�R�͂��Ɍ����ʒ�R��Rf�ɒB���Ă���Ɖ��肵�����Ƃ͑Ó��ł���B
���R�F�Z�o����Sb�̒l�́A��������iSb>6.0mm�j�Ɛ������邽�߁B
���̋L���ւ̃g���b�N�o�b�NURL
https://fanblogs.jp/tb/12703963
���u���O�I�[�i�[�����F�����g���b�N�o�b�N�̂ݕ\������܂��B