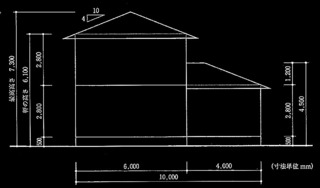
図1〜図3に示す2層2 × 2 スパンの鉄骨造骨組の設計に関する以下の設問に解答せよ。
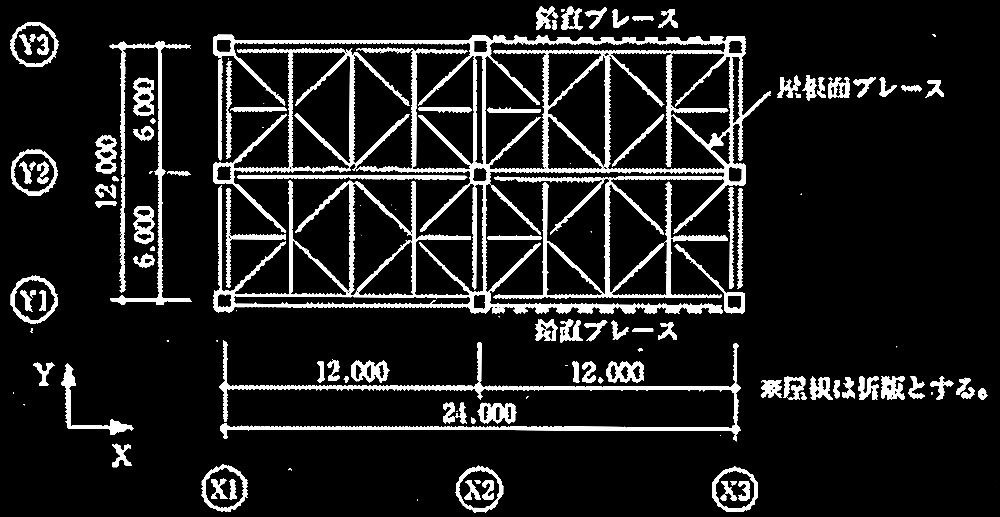
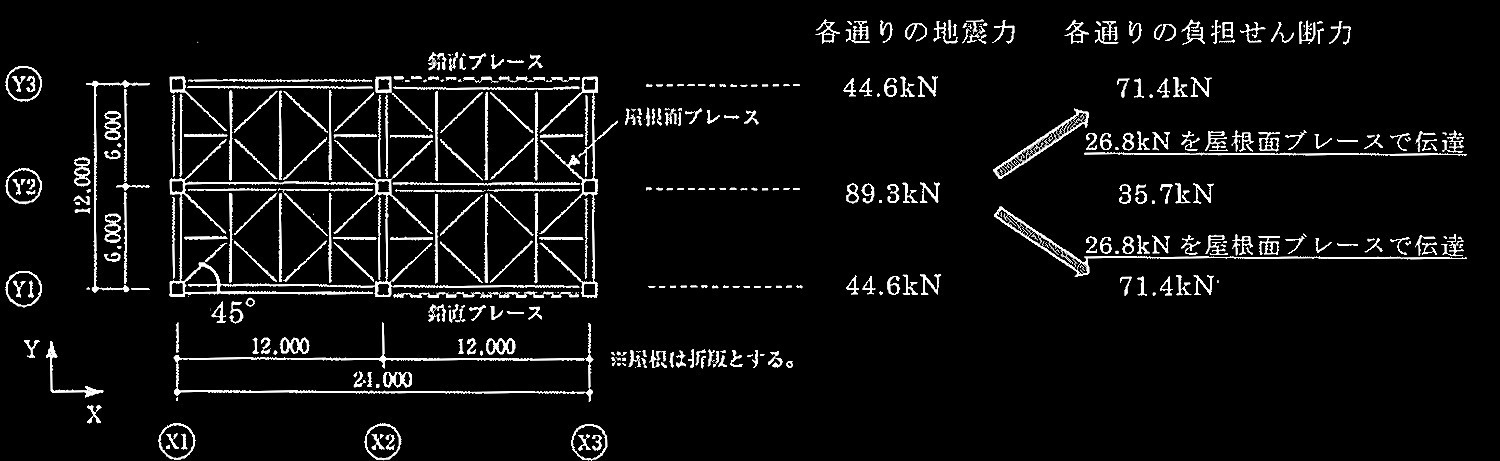
図1 R階伏図 (単位:mm)
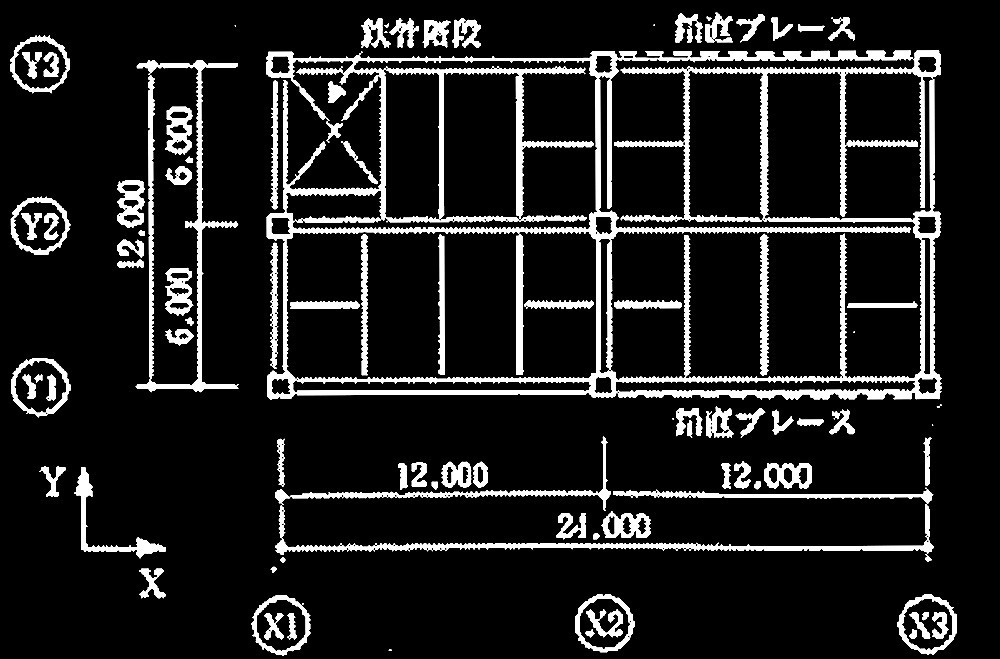
図2 2階伏図 (単位:mm)
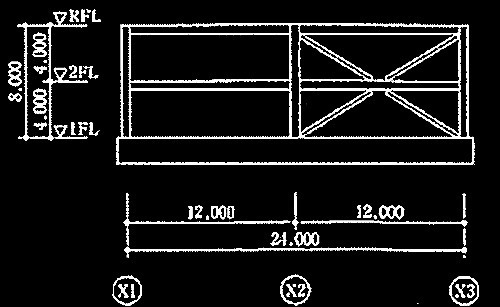
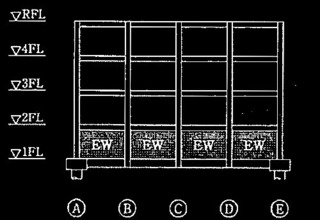
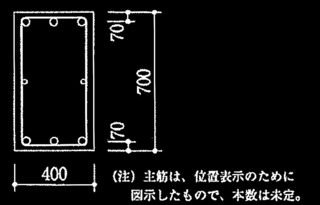
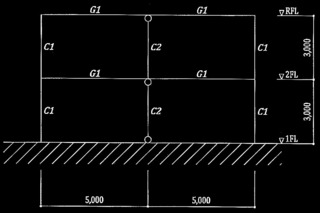
図3 Y1、Y3通り軸組図 (単位:mm)
[ No.1 ]
平成7 (1995)年兵庫県南部地震では、鉄骨造建築物の柱梁接合部における梁端部フランジの完全溶込み溶接部の脆性破壊が多く見られた。一般に、溶接接合部の脆性破壊は特定の条件が同時に満足される場合に限って生じると言われているが、その条件を3つ記述せよ。
答え
[ 解答解説 ]
(例)
・引張応力の存在
・切欠き部の欠損(応力・ひずみ集中源)の存在
・パス間温度管理不足などによる低靱性
[ No.2 ]
2階伏図において、X1通り、Y2〜Y3通り間の大梁には、鉄骨階段があるため、その間はスラブや小梁を設けることができない。このような場合の設計上の留意点及び対策を述べよ。
答え
[ 解答解説 ]
(例)
・解析モデルについて
留意点:他の大梁と異なりスラブがついていないことを、モデル化に適切に反映する。
対 策:モデル化において大梁の曲げ剛性割り増しを考慮しない。剛床仮定を解除する
・断面の検定について
留意点:階段部分に小梁が設けられないことに対して、横座屈長さを適切に評価する
対 策:横座屈長さを階段開口の長さで評価して、許容応力度の設定や保有耐力横補剛の検討を行う
留意点:X1-Y3通りの柱に対して大梁の軸力で地震力が伝達されることを考慮する
対 策:断面の検定において伝達される地震力に対する大梁の軸耐力の検討を行う
留意点:X1通りの外壁に加わる風圧力が大梁の弱軸方向に加わる可能性がある
対 策:大梁の弱軸方向の外力に対して、変形及び強度の検討を行う
外装の取り付け方次第では、ねじれ応力に対しての検討も行う
[ No.3 ]
2階伏図において、Y1通り、X1〜X2通り間の大梁は、小梁によって等間隔に横補剛されていると考えた場合、その補剛間隔が保有耐力横補剛の条件を満足するか否かを、下記の式(1)又は式(2)のいずれか片方の式を用いて検討せよ。どちらの式を用いるかは与条件により判断すること。

答え
[ 解答解説 ]
梁全長にわたって等間隔に横補剛されているため、式(1)を用いる。
・λy = 梁長さ / 弱軸まわりの断面2次半径
= 12,000mm / 70.4mm = 170.4
・nは横補剛(小梁)の箇所数 = 3
130 + 20 × n = 130 + 30 × 3 = 190
λy ≦ 130 + 20 × n より
保有耐力横補剛の条件を満足する。
[ No.4 ]
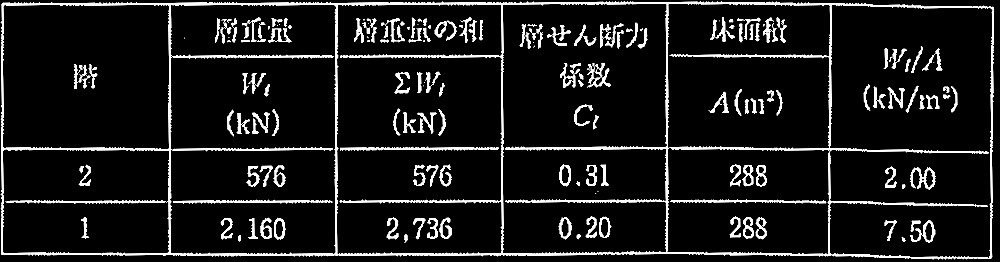
表1に一次設計用地震力算定用の層重量及び層せん断力係数を示す。X方向の地震力に対して、2階各フレームのせん断力の負担率を、Y1及びY3通りがそれぞれ40%、Y2通りが 20%とした場合、屋根面ブレース1本当たりの地震時設計上軸力を求めよ。なお、各通りの地震力算定には、単位床面積当たりの平均重量(Wi/A)を用い、屋根面ブレースは引張ブレースとし、各ブレースは均等に負担するものとする。
表1 一次設計用地震力算定用の層重量及び層せん断力係数
答え
[ 解答解説 ]
階全体の地震力及び、支配幅による各通りの地震力は下記となる。
・階全体の地震力:
ΣQ = ΣWi × Ci
= 576 kN × 0.31 = 178.6kN
・各通りの地震力:
Y1通り及びY3通り
支配面積 = 24m × 6m/2 =72m2
地震力 = Wi/A × 支配面積 × Ci
= 2.0 kN/m2 × 72 m2 × 0.31
= 44.6 kN
Y2通り
支配面積 = 24m × 6m = 144m2
地震力 = Wi/A × 支配面積 × Ci
= 2.0 kN/m2 × 144m2 × 0.31
= 89.3 kN
・各フレームの負担せん断力:
Y1通り及びY3通り
ΣQ の40% = 178.6 × 0.4 = 71.4kN
Y2通り
ΣQの20% = 178.6 × 0.2 =35.7 KN
・屋根面ブレースで伝達される地震力は、各通りの地震力と各フレームの負担せん断力の差で求める。
Y2通りから、Y1,Y3通りへ移行する地震力:
ΣQB = 71.4 kN – 44.6kN = 26.8 kN
屋根面ブレース1本あたりの負担地震力:
QB = ΣQB / ブレース台数
= 26.8kN / 4 = 6.7 kN
・屋根面ブレース1本当たりの地震時設計用軸力 NB
ブレース角度は 45° であるから、
NB = QB/cos45° =6.7kN / cos45° =9.5 kN