新規記事の投稿を行うことで、非表示にすることが可能です。
2023年04月21日
08034 大人のさび落とし 図形と方程式 領域での最大・最小
大人のさび落とし
図形と方程式 領域での最大・最小
01
領域を 表す式が与えられていて
その領域内を
点(x、y)が 動くとき
y+2xの 最大 ・ 最小を
求めてちょうだい。

02
まず 領域を 見える様に
絶対値が 苦手な方も
けっこう いらっしゃいますが
慣れだからさ
絶対値が ついてるがために
答は 正なんですが
絶対値が付いてないと
中味がじゃナイスカ
負の時と 正の時があるですので

03
少し整理して
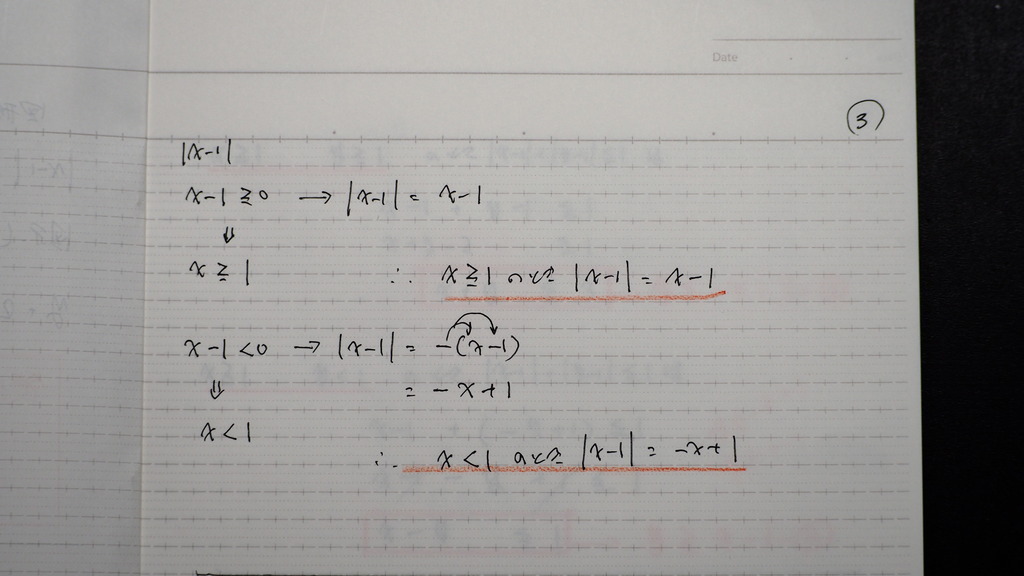
04
こんな感じに
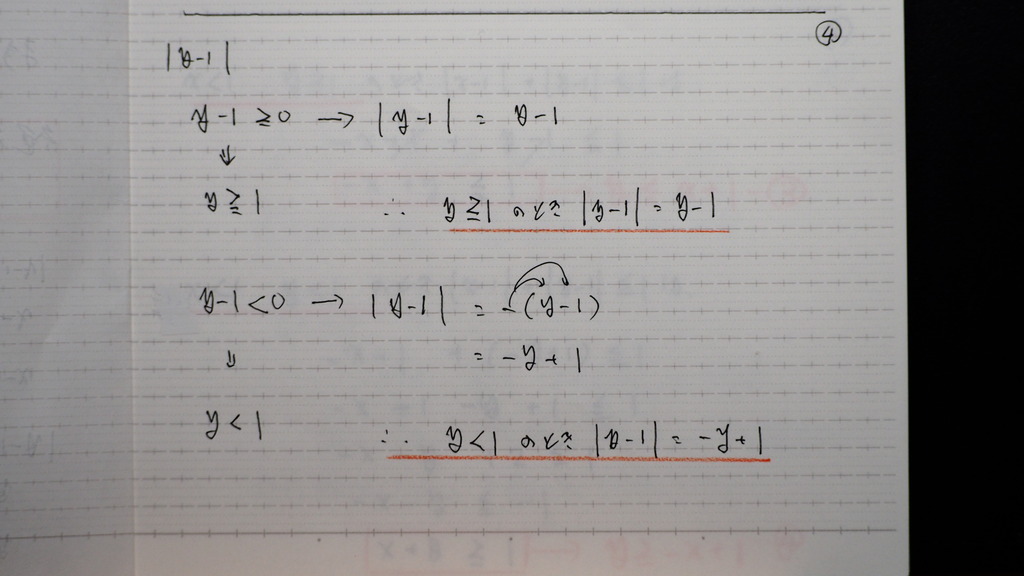
05
さらに 少し整理して
傾きと y切片が わかる形にして

06
わたしんとこは
子供は
学校も出ずに
毛皮を着て
猫っていうんですが
9匹のメス
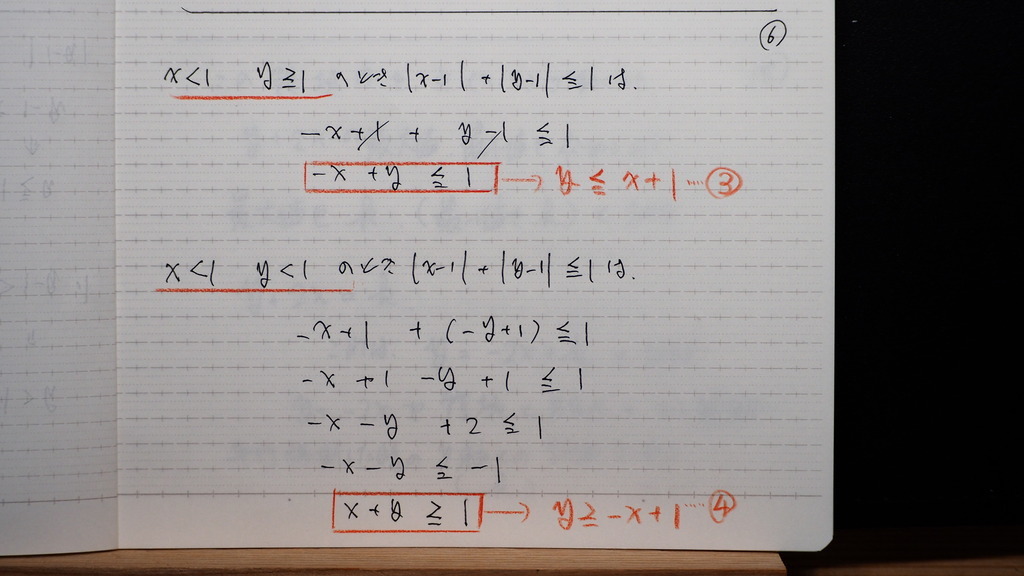
07
話を 元に戻して
こんな感じに
整理できました
これが
与式の 表す領域ですよ
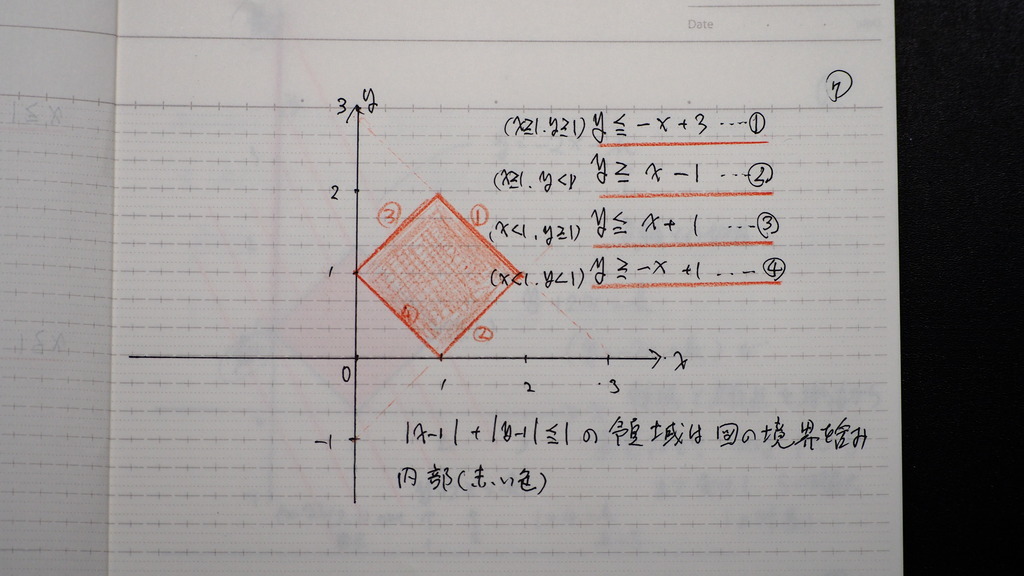
08
ここから
y+2xの 最大・最小を
求めるんですが
=kと置いて
式を ちょっと 書き換えると
kは
y切片で
出てくるとわかるので

09
y=-2x+kを
領域を通る様に
( x、y) が 領域内を
動くとき
kが 最大と 最小に なるとこを
見ると

10
答は こんな感じで
さっきの 横道ですが
我々世代は
息子 娘が 大人になってるか
遅かった人は
学生 真っ只中か
な感じですか
コロナの ダメージから
何とか 這い上がりたい
この頃ですね
身も 体も 心も 経済も

11
るいだい
ラーメン大学で
味噌バタ コーントッピングって
いま いくらかな
タクシー乗ってますか?
すみません
にたような 問題です

12
大雑把に ここら辺のなかの
後 二つ 不等式を
書き込むと
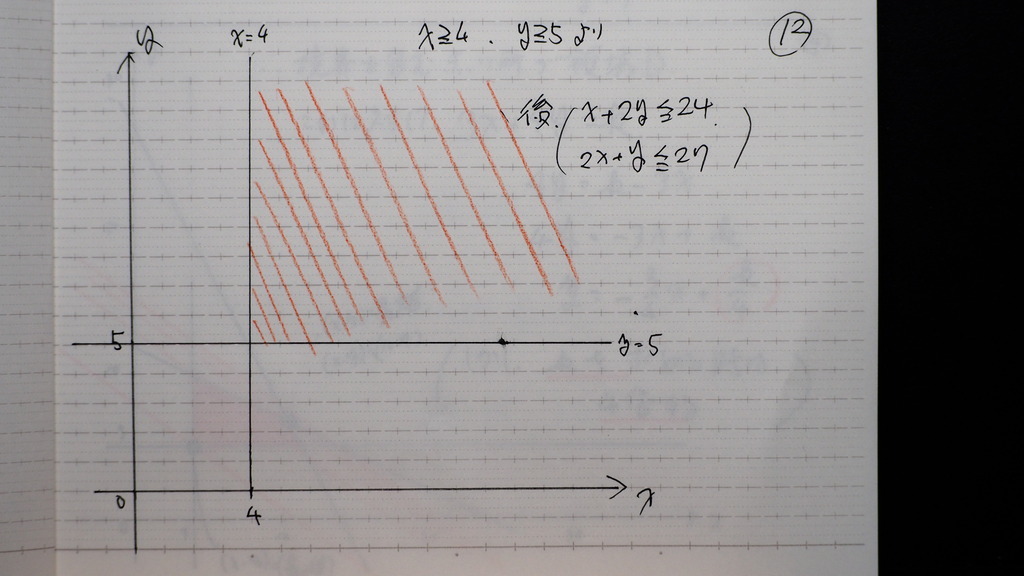
13
こんなだから

14
こんな感じか
ここと ここを 通るとき
最大 最小

15
数字が 偉く 大きくなってるけど
式変形したときに
最大 ・ 最小 を
求める
直線の式の y切片が
k/4 になってるので
元の 式に x、yを
代入したらば
4倍だからさ
これでいいんだけど
高校とかの 物理で
なんかの 問題を
解いていて
答が すごく おおきく 成っちゃって
せんせ 曰く 偉い 大きいな
誰か 電卓 持ってるか?
勉強するとき 別に
使ってもいいからさ
あ だいじょうぶだな

16
また 少し 横に行ってましたが
これです

17
これも 類題
領域を 求めて
最大・ 最小のとこが
表現が 変わっただけ

18
先ず 領域を
求めて
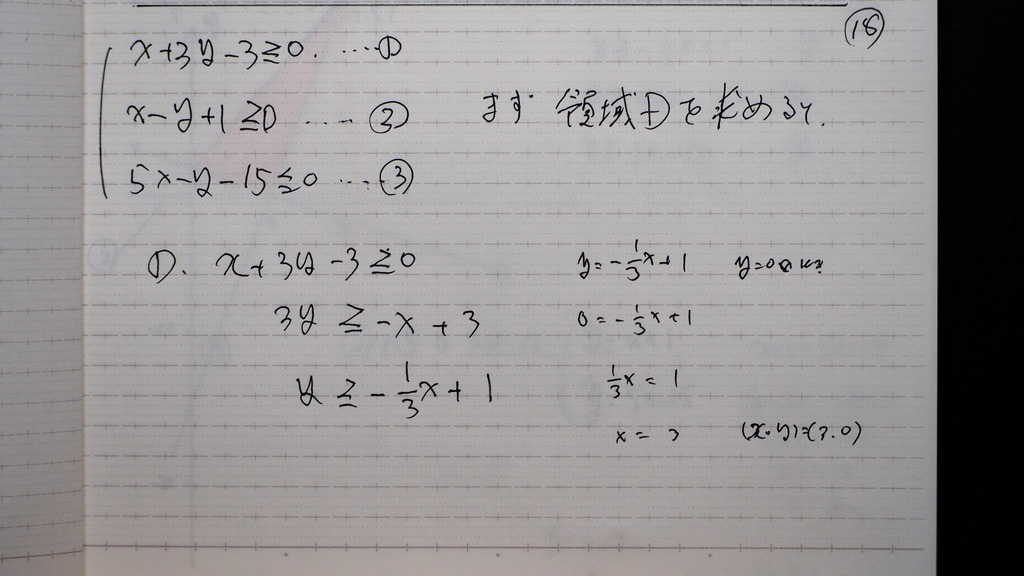
19
傾きと切片が わかる形で
グラフを 作ると
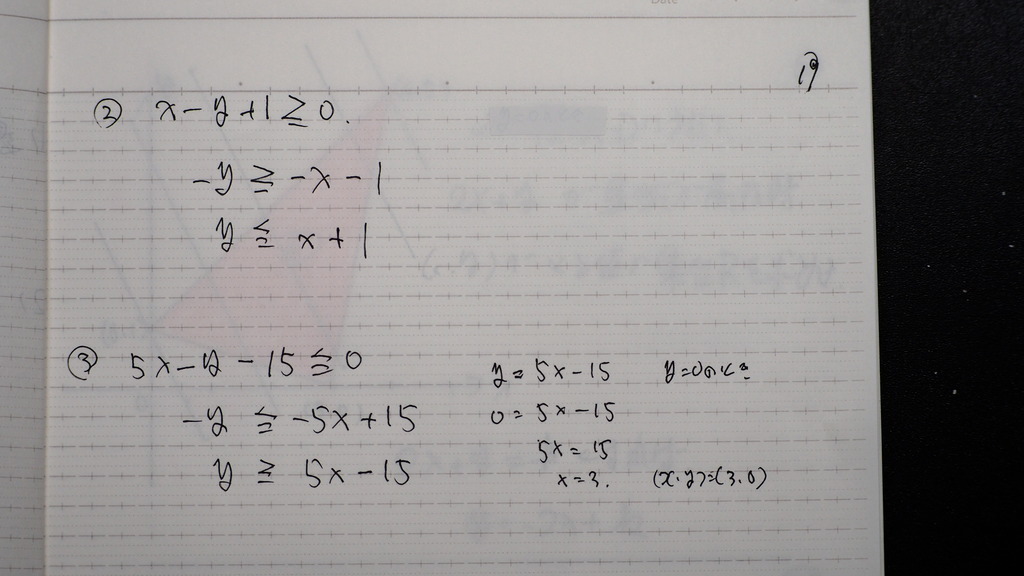
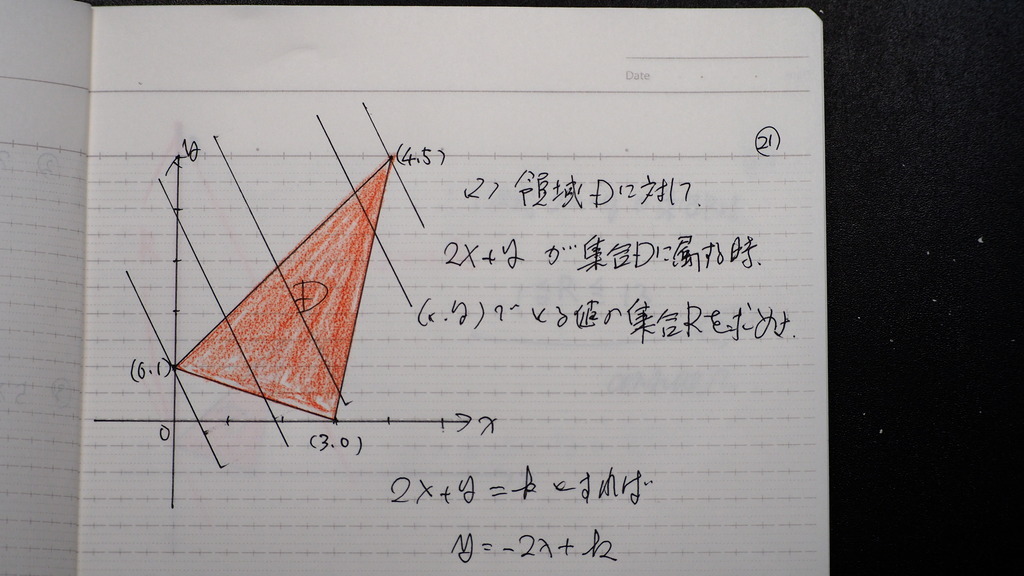
20
こんなで
②と③の 交点は(4,5)
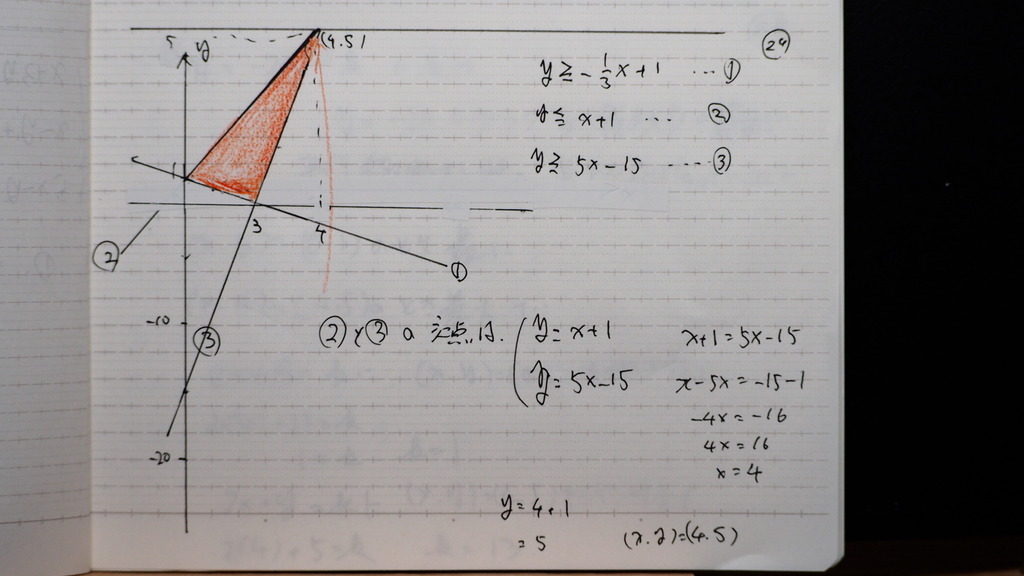
21
一次 式に領域の (x、y)を
代入してくと
y切片が
変わってくる
その 軌跡が y軸に できるんですが
それが R じゃナイスカ
22
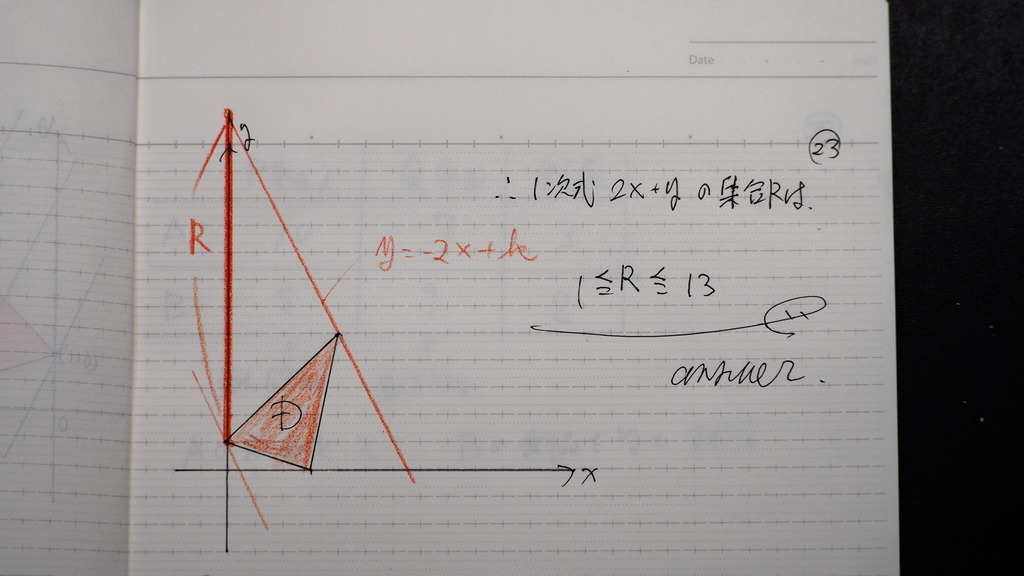
ここから ここまでを
計算して

23
こんな感じで
集合R だから R{ t | 1 レスザンイコール t レスザンイコール 13}
って書かないといけない。
24
ある工場で
製品を 2種類作っているんだって
ソレゾレ 同じ2つの原料を
割合を 変えて 作っていて
1単位作るのための 必要度と
利益は
表のようになっているんだって
最大利益を
出すには
ソレゾレ 何単位づつ
作ったらよいか

25
これがさ
表

26
表を 縦に見て
A と Bで
Pは 65キログラム
Qは 84キログラム
まで
利益を kとすれば

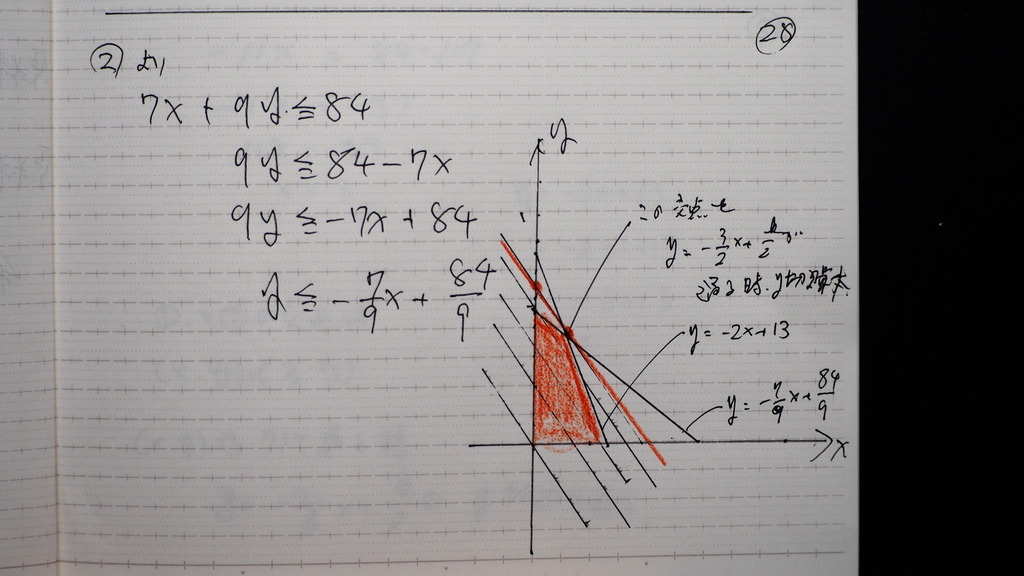
27
グラフにして

28
最大 利益を 出すには
2つの式の 交点になってるとこの
x、y の 値を
代入すると
29
交点は
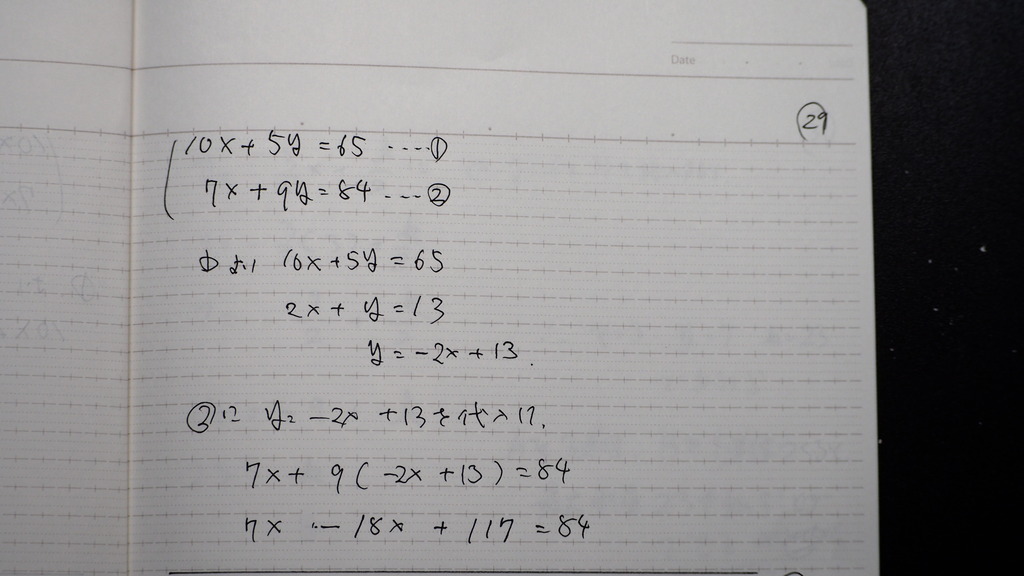
30
(3,7)
であるので
xは A yはB
としたので
Aを3単位 Bを7単位
作ると
最大利益になる

31
こんな感じですか

お疲れ様です。
図形と方程式 領域での最大・最小
01
領域を 表す式が与えられていて
その領域内を
点(x、y)が 動くとき
y+2xの 最大 ・ 最小を
求めてちょうだい。
02
まず 領域を 見える様に
絶対値が 苦手な方も
けっこう いらっしゃいますが
慣れだからさ
絶対値が ついてるがために
答は 正なんですが
絶対値が付いてないと
中味がじゃナイスカ
負の時と 正の時があるですので
03
少し整理して
04
こんな感じに
05
さらに 少し整理して
傾きと y切片が わかる形にして
06
わたしんとこは
子供は
学校も出ずに
毛皮を着て
猫っていうんですが
9匹のメス
07
話を 元に戻して
こんな感じに
整理できました
これが
与式の 表す領域ですよ
08
ここから
y+2xの 最大・最小を
求めるんですが
=kと置いて
式を ちょっと 書き換えると
kは
y切片で
出てくるとわかるので
09
y=-2x+kを
領域を通る様に
( x、y) が 領域内を
動くとき
kが 最大と 最小に なるとこを
見ると
10
答は こんな感じで
さっきの 横道ですが
我々世代は
息子 娘が 大人になってるか
遅かった人は
学生 真っ只中か
な感じですか
コロナの ダメージから
何とか 這い上がりたい
この頃ですね
身も 体も 心も 経済も
11
るいだい
ラーメン大学で
味噌バタ コーントッピングって
いま いくらかな
タクシー乗ってますか?
すみません
にたような 問題です
12
大雑把に ここら辺のなかの
後 二つ 不等式を
書き込むと
13
こんなだから
14
こんな感じか
ここと ここを 通るとき
最大 最小
15
数字が 偉く 大きくなってるけど
式変形したときに
最大 ・ 最小 を
求める
直線の式の y切片が
k/4 になってるので
元の 式に x、yを
代入したらば
4倍だからさ
これでいいんだけど
高校とかの 物理で
なんかの 問題を
解いていて
答が すごく おおきく 成っちゃって
せんせ 曰く 偉い 大きいな
誰か 電卓 持ってるか?
勉強するとき 別に
使ってもいいからさ
あ だいじょうぶだな
16
また 少し 横に行ってましたが
これです
17
これも 類題
領域を 求めて
最大・ 最小のとこが
表現が 変わっただけ
18
先ず 領域を
求めて
19
傾きと切片が わかる形で
グラフを 作ると
20
こんなで
②と③の 交点は(4,5)
21
一次 式に領域の (x、y)を
代入してくと
y切片が
変わってくる
その 軌跡が y軸に できるんですが
それが R じゃナイスカ
22
ここから ここまでを
計算して
23
こんな感じで
集合R だから R{ t | 1 レスザンイコール t レスザンイコール 13}
って書かないといけない。
24
ある工場で
製品を 2種類作っているんだって
ソレゾレ 同じ2つの原料を
割合を 変えて 作っていて
1単位作るのための 必要度と
利益は
表のようになっているんだって
最大利益を
出すには
ソレゾレ 何単位づつ
作ったらよいか
25
これがさ
表
26
表を 縦に見て
A と Bで
Pは 65キログラム
Qは 84キログラム
まで
利益を kとすれば
27
グラフにして
28
最大 利益を 出すには
2つの式の 交点になってるとこの
x、y の 値を
代入すると
29
交点は
30
(3,7)
であるので
xは A yはB
としたので
Aを3単位 Bを7単位
作ると
最大利益になる
31
こんな感じですか
お疲れ様です。