新規記事の投稿を行うことで、非表示にすることが可能です。
2023年03月28日
08031 大人のさび落とし 図形と方程式 領域(2)
図形と方程式 大人のさび落とし
01
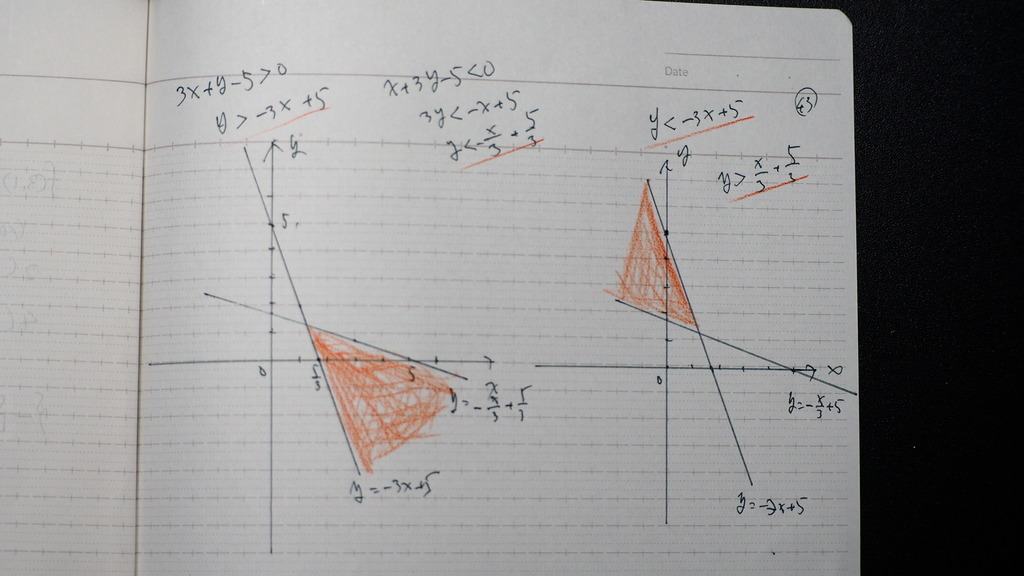
次の ような 不等式の 領域を
図示せよ
直線 y=mx+2が 2点
A(3,2) B(-1、4)
を 結ぶ線分と 交わるときの
mの範囲を 求めよ

02
可能性としてじゃナイスカ
プラス・マイナス
マイナス・プラス
であるから
まず 大きく 2つに場合分け

03
集合M と 集合N とするでしょ
Mの中の➀②
Nの中の③④
の 共通領域 を
合わせたものが
求める 領域になるので
➀キャップ②:M
③キャップ④:N
M カップ N
(➀キャップ②) カップ (③キャップ④)

04
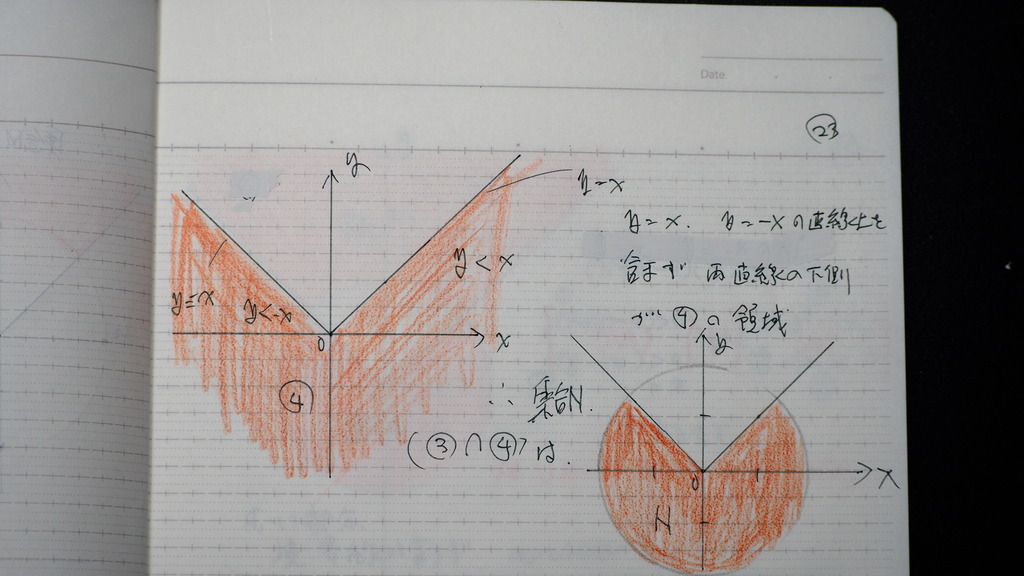
集合Mの ②の方は
円の方程式で
中心が 原点 半径 1の
周上 および 内部
➀の方は
絶対値があるので
絶対値を プラスで 外すとき
絶対値を マイナスで 外すとき

05
プラスで 外すとき
マイナスで 外すとき
絶対値の 中味の Aを
挟む かたちにして
Aの 符号を
正にすると
なるでしょ

06
であるから
集合Mの方の
共通領域は
これらの 共通部分

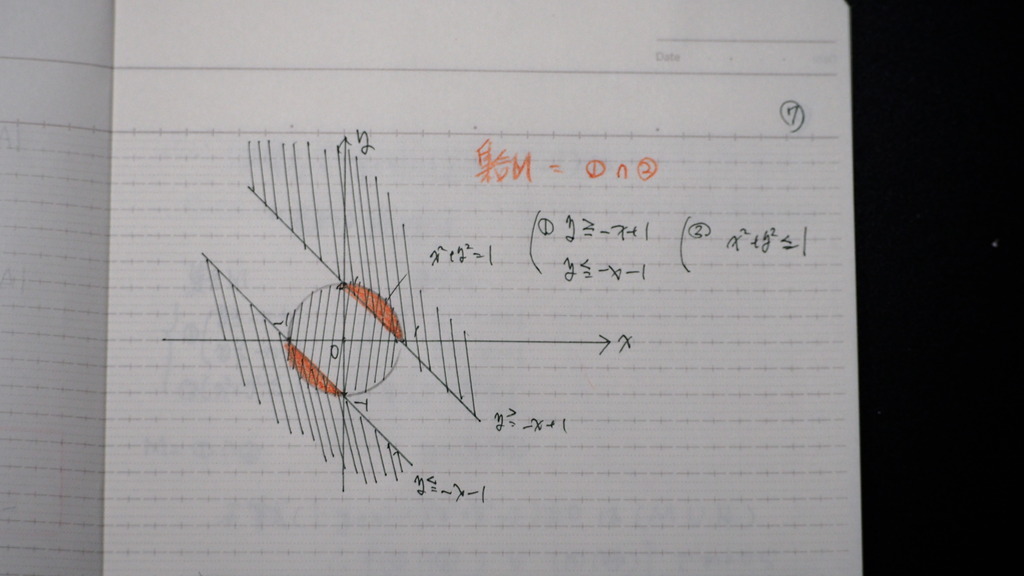
07
ここです
円の 内部と
直線の 下と 上
08
集合Nの方は
絶対値は
こんな感じで
こんどは円の外側

09
であるから
まとめると
与式は
二つの 可能性に 場合分けで来て
その M と N の 集合を
合わせたものが
領域になるから

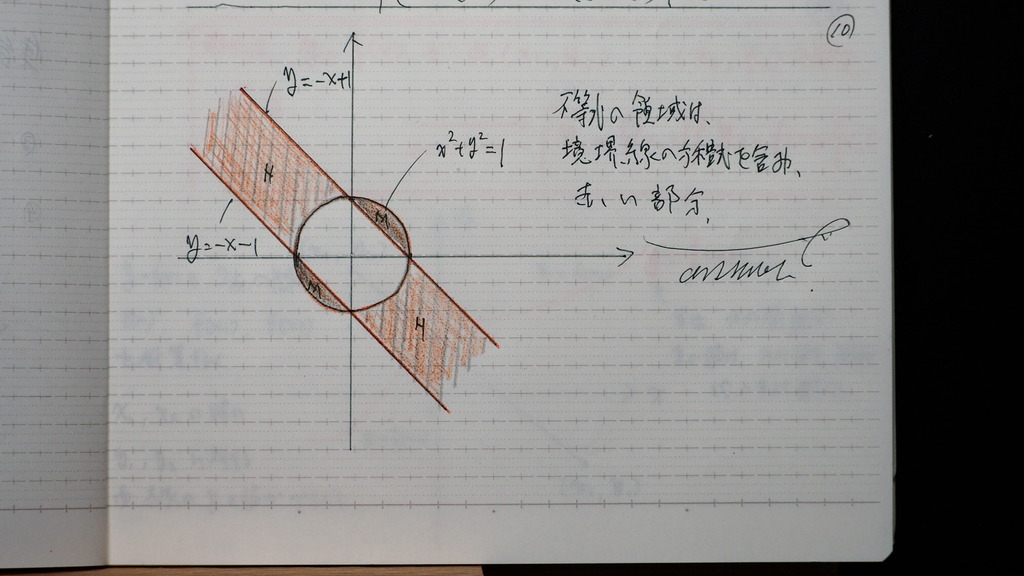
10
こんな 形で
境界線を 含み 赤い所
堺 の 字が
間違ってました
こっち 界
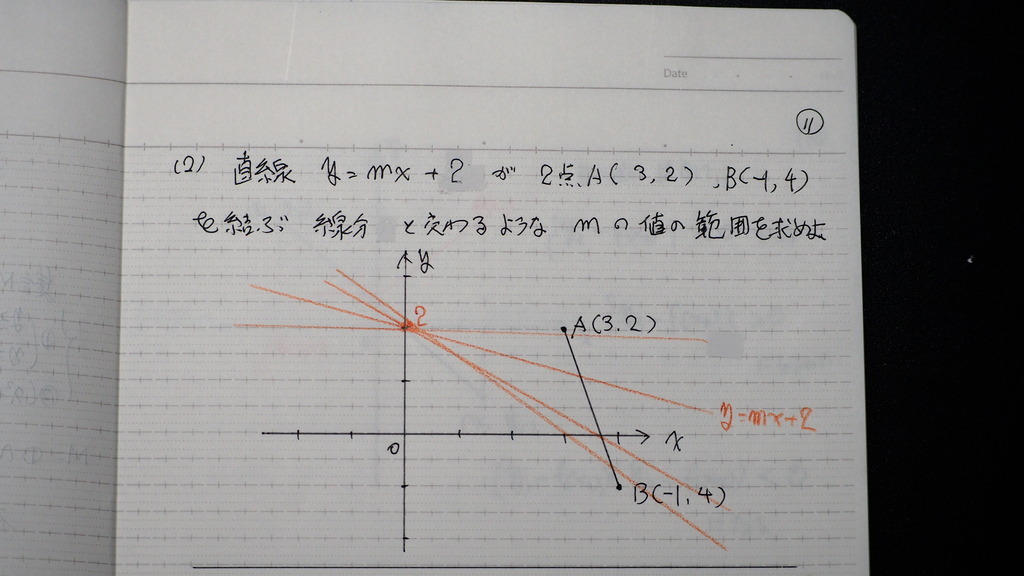
11
かっこ 2は
直線が 線分と 交わると
その時に
12
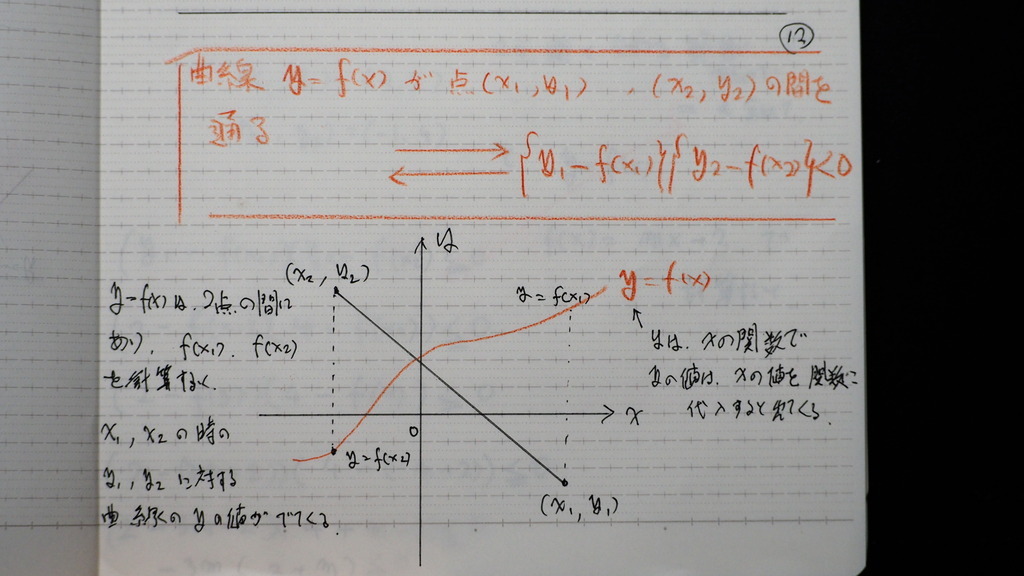
曲線が 線分を 突っ切てると
線分の 両端の 座標
の x と y の yは
曲線上の xに 対応する
曲線上のy つまり f(x)
と 大きさを
比べると
y1-f(x1)
y2-f(x2)
一方の端が プラスならば
他方の端は マイナス
であるから
曲線 直線が 線分と 交わる領域は
この二つの 積が
マイナス か 等しい所
13
こんな感じに表現できるので
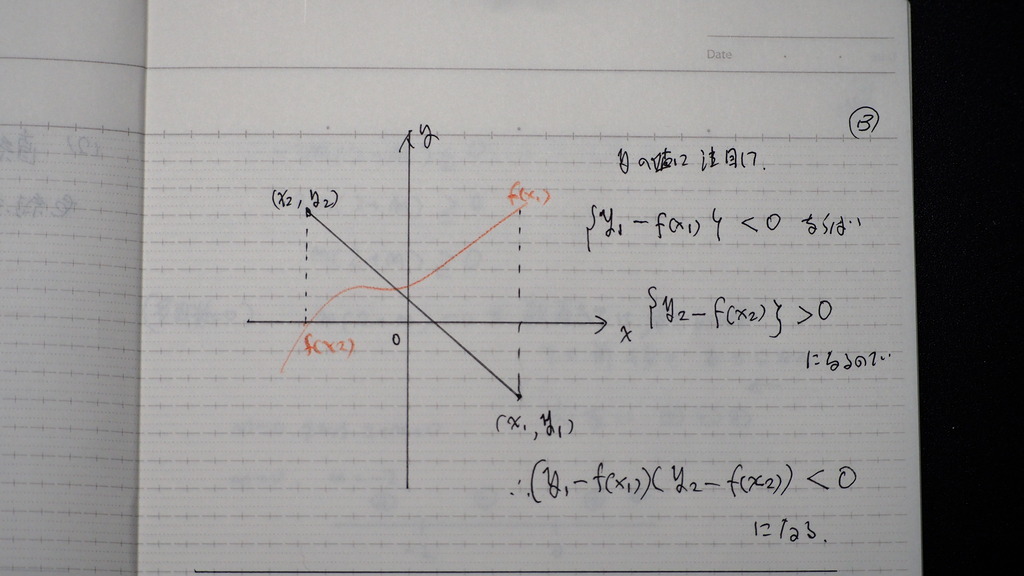
14
これを 計算するじゃナイスカ

15
不等式が
わかんなくなった時は
各因数が ゼロ になるとこを
数直線に 書き込んで
その前後を
交互に
左 ← 右
右から左に
+ - +

16
不等式が
ゼロ 以上になってるとこは
ここ
これが m の 値の範囲
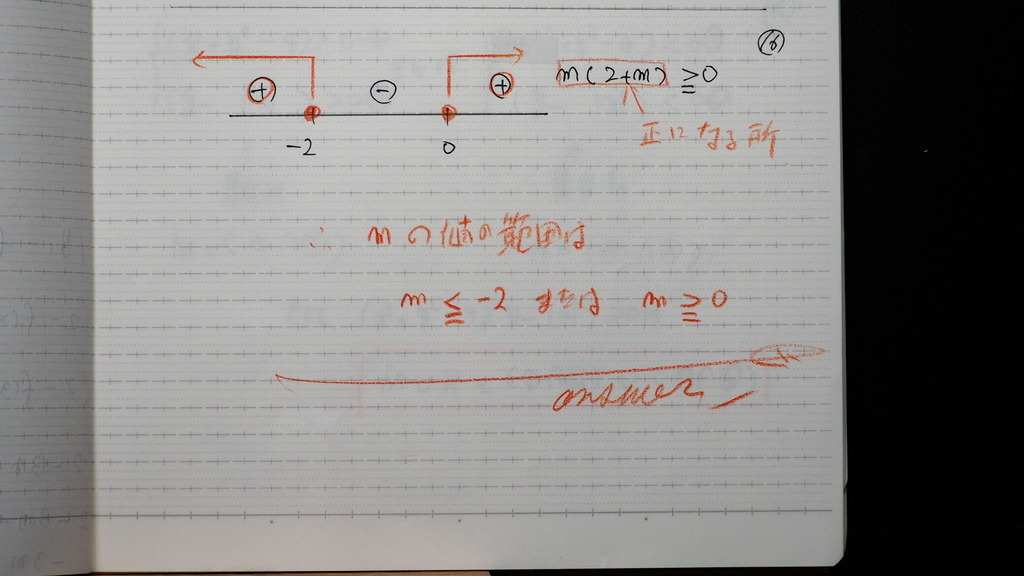
17
では 類題行ってみましょう

18
場合分け
それぞれの 共通領域を
合わせたものが
求める 領域

19
集合Mの方は
円の 方程式は
円の外側

20
絶対値は
こんな感じに なるので
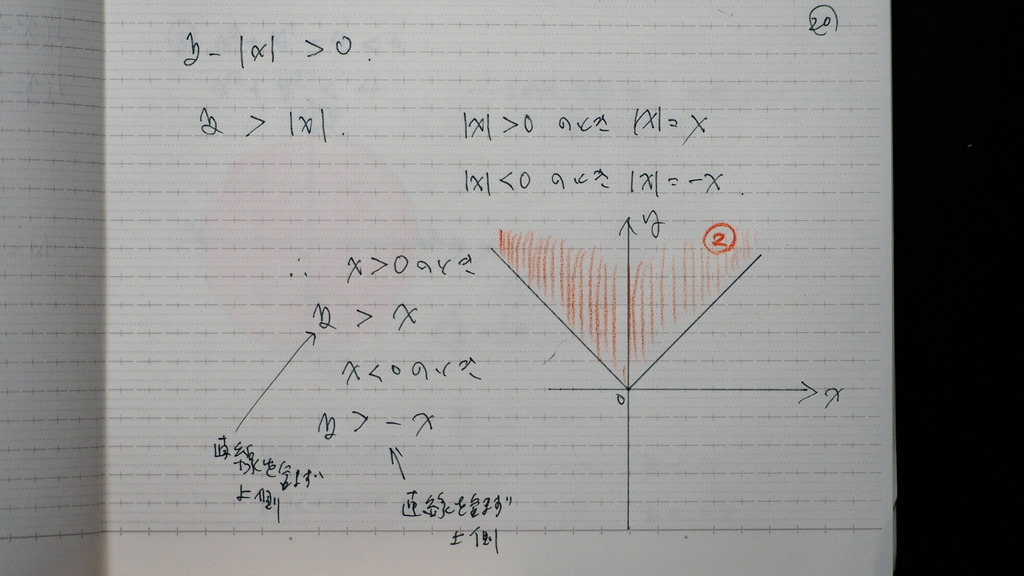
21
場合分け 集合Mは
ここ 赤い所
境界線含まず
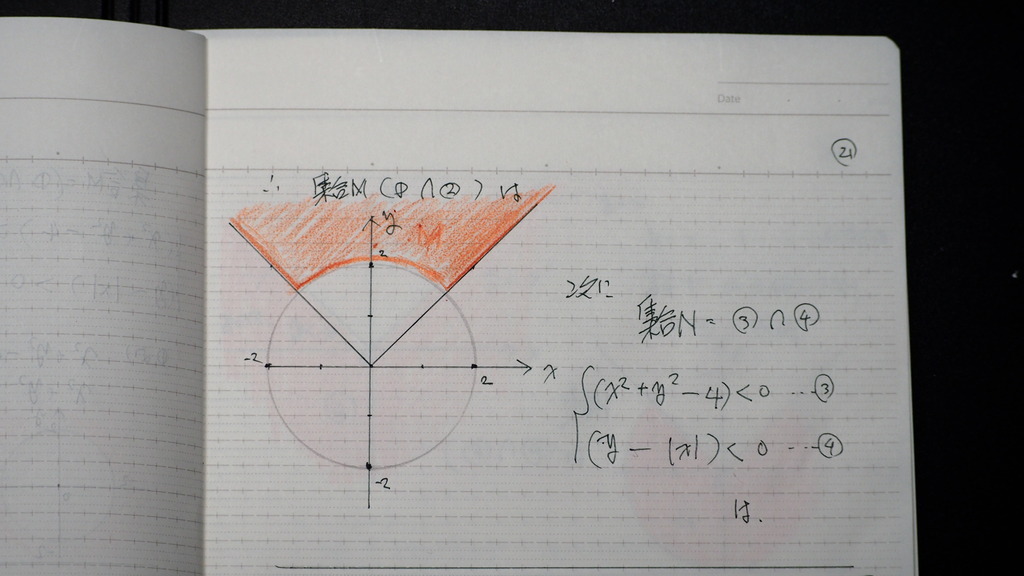
22
集合Nは
円の内部と

23
こんな感じなので
24
まとめると
与式は
大きく 2つに 場合分けで来て
それぞれの 共通部分を
合わせると
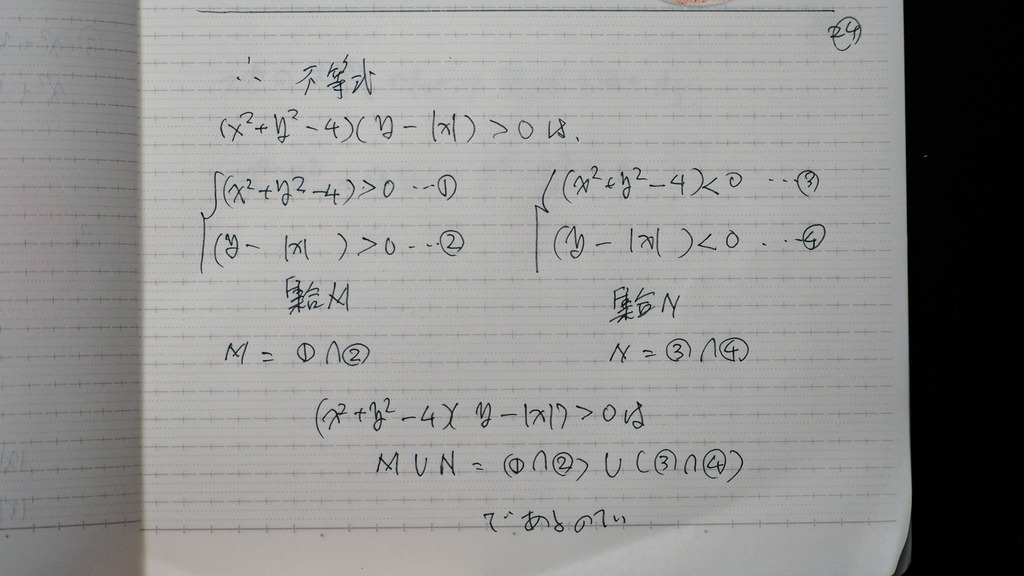
25
こんな感じに
なるですよ
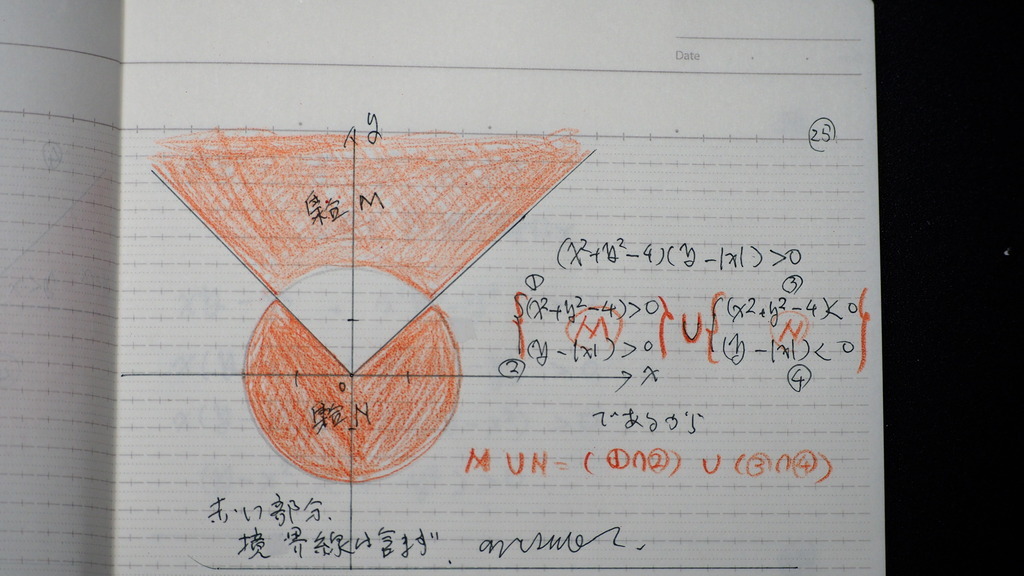
26
次の
不等式のあらわす
領域を 図示せよ

27
先ず 因数分解
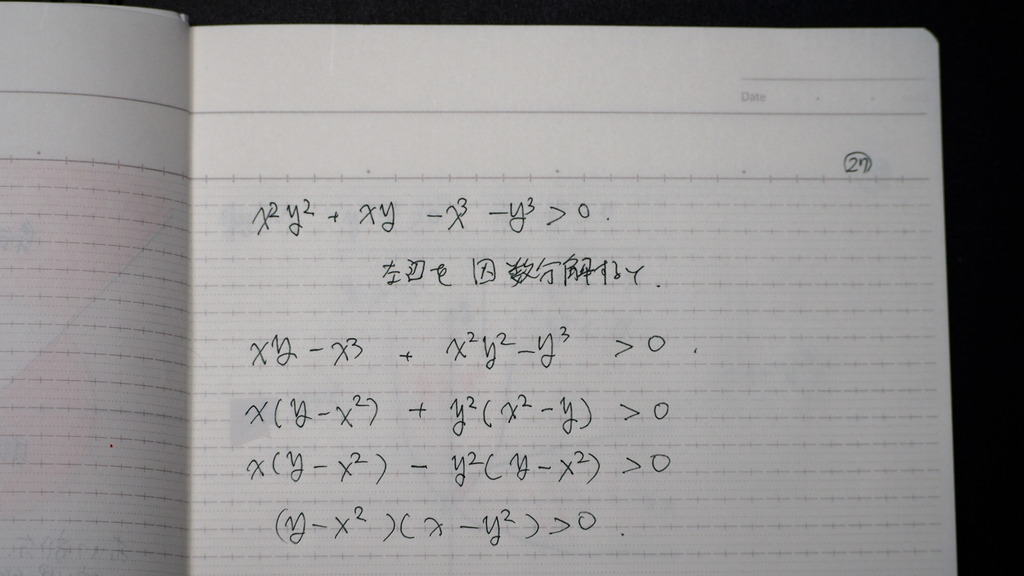
28
因数分解が できれば
場合分け
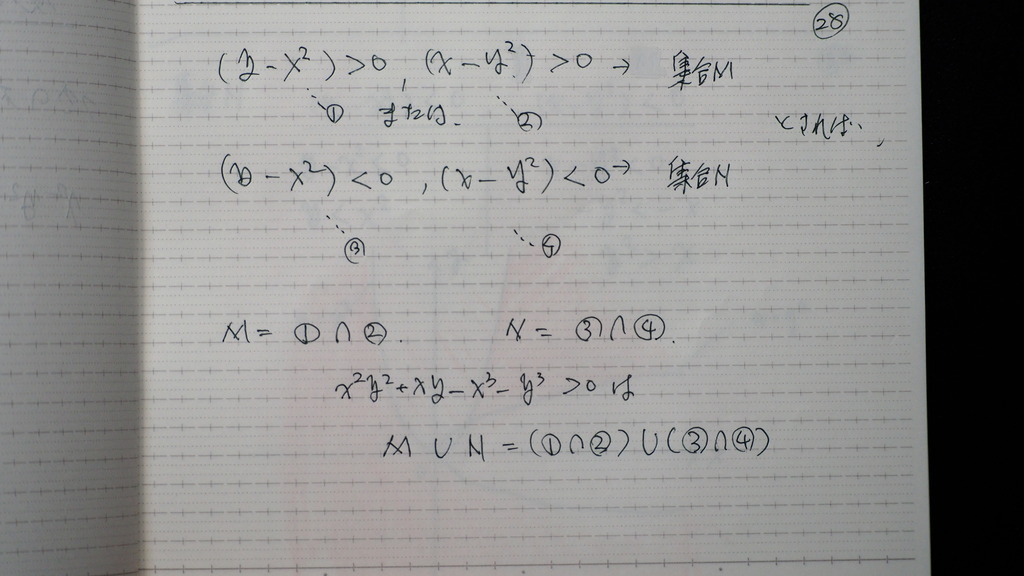
29
集合 ん~
大丈夫かな
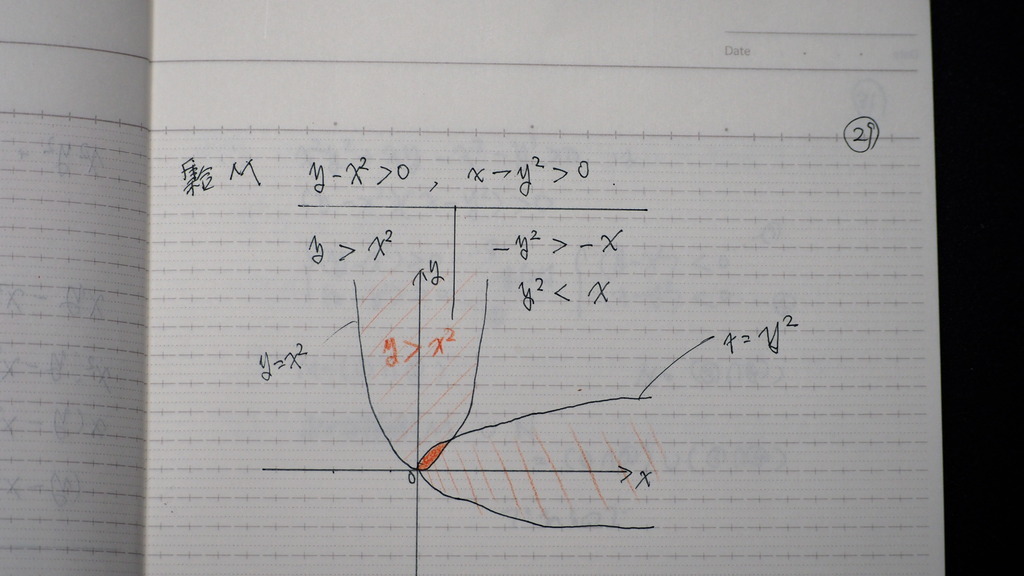
30
こう言うさー
問題なんだけどさ
いま やってるんはさ
すうがくだ~からさ
え わかってる
それなら い いんだけどさ
ホントに 大丈夫かな
だから なんなんだ
赤い所
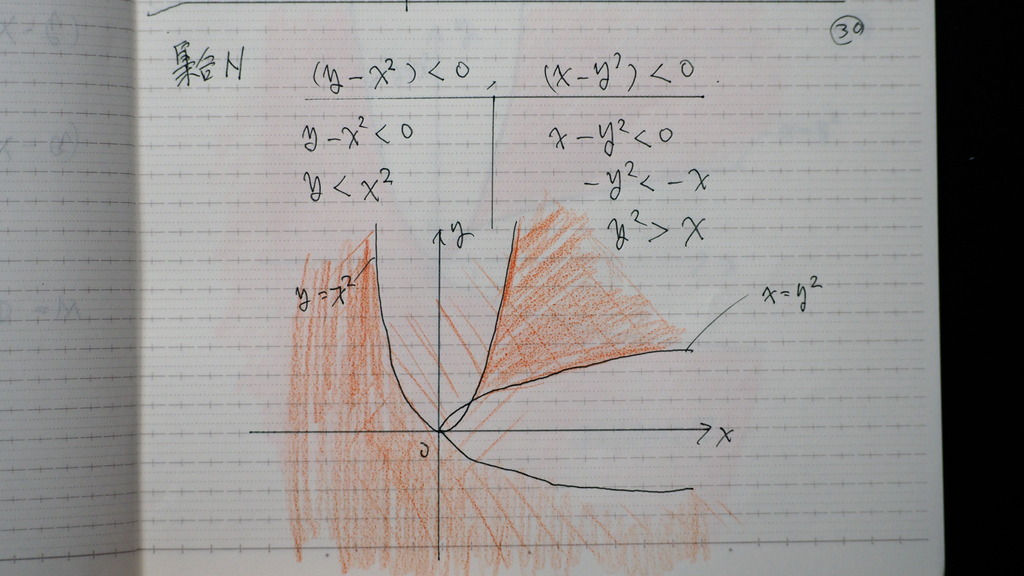
31
だから
まとめると
なので

32
これだ
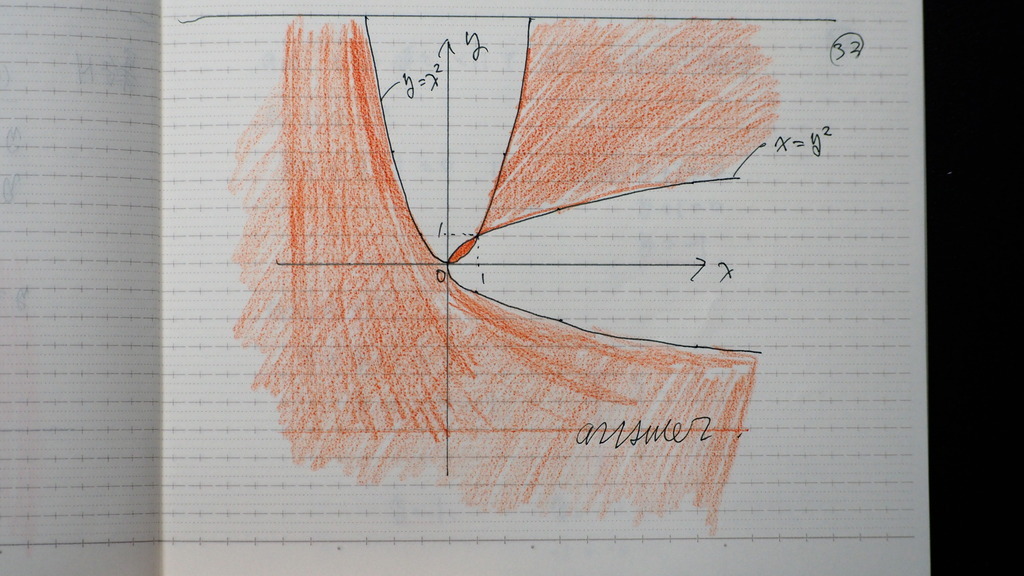
33
ぐわいわり
えーと
問題
読んでいただいて

34
定点の座標から
どんな 値でも いいって言ってるから
都合のいいとこを
2っつ 持ってきて

35
コレダ
で
与式を 変形と言うか
f(x)= に替えてじゃナイスカ
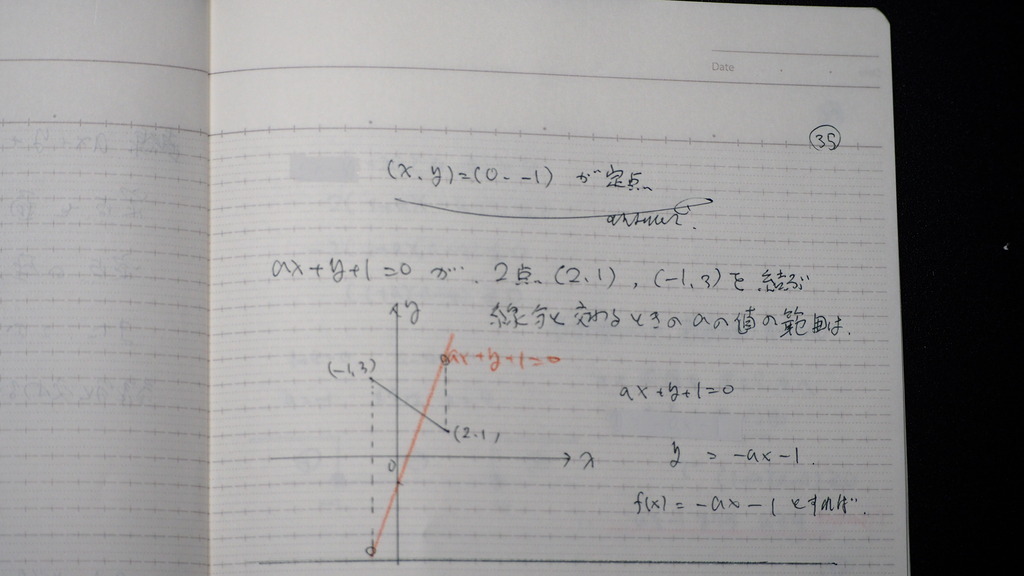
36
直線が 線分と交わるときの
領域の 求め方で

37
これを 解けば

38
最後は
2点が 在って
一方が 円の 内側
他方が 円の 外側
になる
円の 中心座標の 領域を
求めよ
円の 方程式は これなんだって
そこで

39
f(x、y)= にすれば
で
2点を代入したものが
領域の 外と 内 なので
積が マイナス
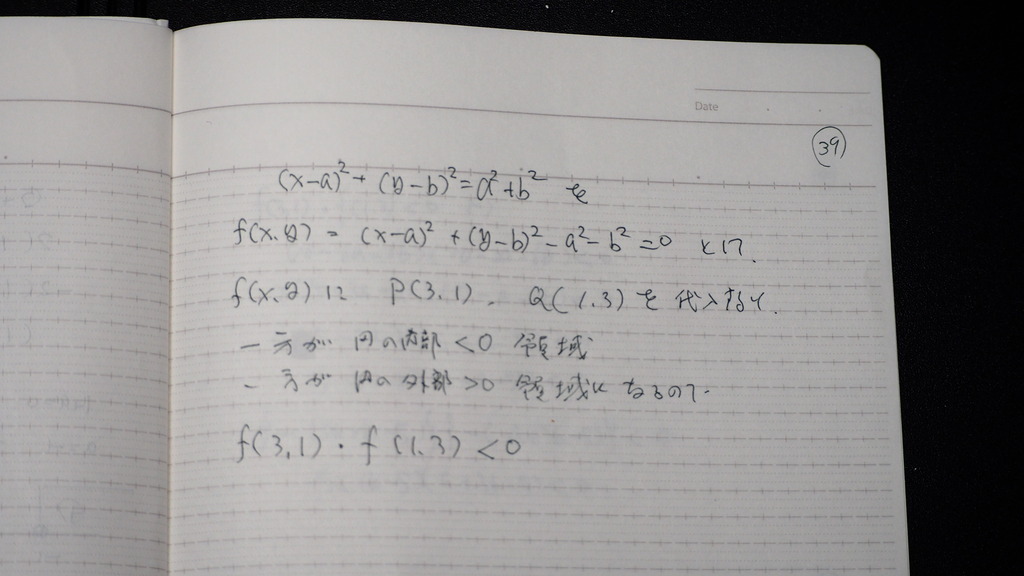
40
これを 計算すると
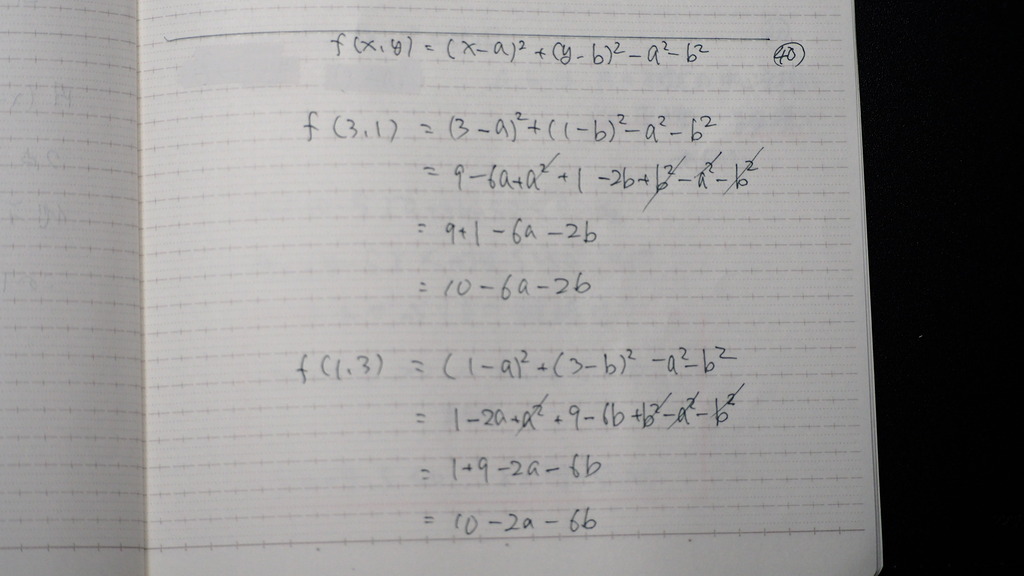
41
二つの 積が マイナス
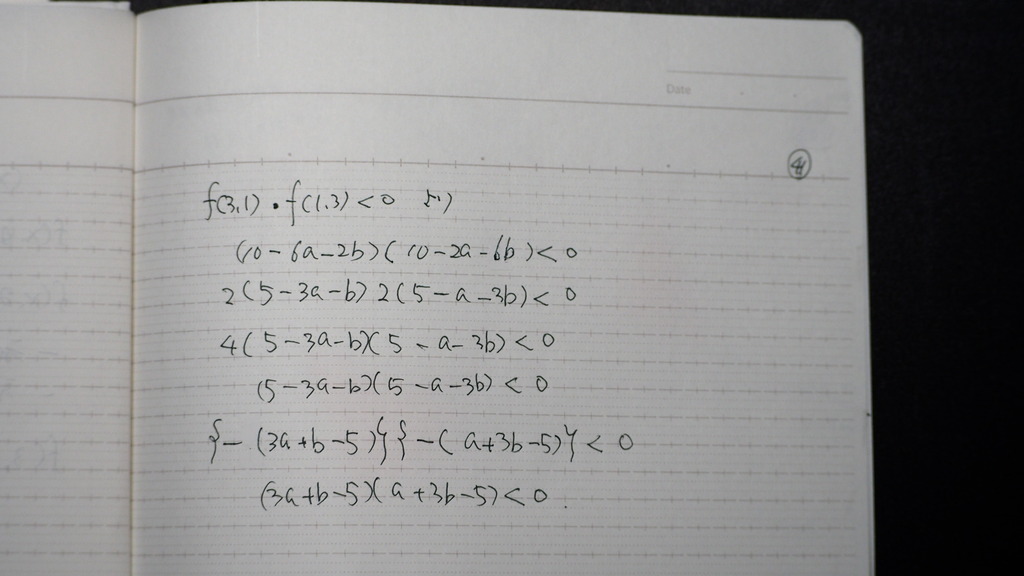
42
ところで
ここでいうところの
a,bは
それぞれ
円の 中心の
x座標 y座標
であるので
x、y を a,bに 代入して
今までのように
領域を
場合分けして
求めると

43
それぞれ
こんなだから
44
こんな感じに なるんだって

お疲れ様です。
01
次の ような 不等式の 領域を
図示せよ
直線 y=mx+2が 2点
A(3,2) B(-1、4)
を 結ぶ線分と 交わるときの
mの範囲を 求めよ
02
可能性としてじゃナイスカ
プラス・マイナス
マイナス・プラス
であるから
まず 大きく 2つに場合分け
03
集合M と 集合N とするでしょ
Mの中の➀②
Nの中の③④
の 共通領域 を
合わせたものが
求める 領域になるので
➀キャップ②:M
③キャップ④:N
M カップ N
(➀キャップ②) カップ (③キャップ④)
04
集合Mの ②の方は
円の方程式で
中心が 原点 半径 1の
周上 および 内部
➀の方は
絶対値があるので
絶対値を プラスで 外すとき
絶対値を マイナスで 外すとき
05
プラスで 外すとき
マイナスで 外すとき
絶対値の 中味の Aを
挟む かたちにして
Aの 符号を
正にすると
なるでしょ
06
であるから
集合Mの方の
共通領域は
これらの 共通部分
07
ここです
円の 内部と
直線の 下と 上
08
集合Nの方は
絶対値は
こんな感じで
こんどは円の外側
09
であるから
まとめると
与式は
二つの 可能性に 場合分けで来て
その M と N の 集合を
合わせたものが
領域になるから
10
こんな 形で
境界線を 含み 赤い所
堺 の 字が
間違ってました
こっち 界
11
かっこ 2は
直線が 線分と 交わると
その時に
12
曲線が 線分を 突っ切てると
線分の 両端の 座標
の x と y の yは
曲線上の xに 対応する
曲線上のy つまり f(x)
と 大きさを
比べると
y1-f(x1)
y2-f(x2)
一方の端が プラスならば
他方の端は マイナス
であるから
曲線 直線が 線分と 交わる領域は
この二つの 積が
マイナス か 等しい所
13
こんな感じに表現できるので
14
これを 計算するじゃナイスカ
15
不等式が
わかんなくなった時は
各因数が ゼロ になるとこを
数直線に 書き込んで
その前後を
交互に
左 ← 右
右から左に
+ - +
16
不等式が
ゼロ 以上になってるとこは
ここ
これが m の 値の範囲
17
では 類題行ってみましょう
18
場合分け
それぞれの 共通領域を
合わせたものが
求める 領域
19
集合Mの方は
円の 方程式は
円の外側
20
絶対値は
こんな感じに なるので
21
場合分け 集合Mは
ここ 赤い所
境界線含まず
22
集合Nは
円の内部と
23
こんな感じなので
24
まとめると
与式は
大きく 2つに 場合分けで来て
それぞれの 共通部分を
合わせると
25
こんな感じに
なるですよ
26
次の
不等式のあらわす
領域を 図示せよ
27
先ず 因数分解
28
因数分解が できれば
場合分け
29
集合 ん~
大丈夫かな
30
こう言うさー
問題なんだけどさ
いま やってるんはさ
すうがくだ~からさ
え わかってる
それなら い いんだけどさ
ホントに 大丈夫かな
だから なんなんだ
赤い所
31
だから
まとめると
なので
32
これだ
33
ぐわいわり
えーと
問題
読んでいただいて
34
定点の座標から
どんな 値でも いいって言ってるから
都合のいいとこを
2っつ 持ってきて
35
コレダ
で
与式を 変形と言うか
f(x)= に替えてじゃナイスカ
36
直線が 線分と交わるときの
領域の 求め方で
37
これを 解けば
38
最後は
2点が 在って
一方が 円の 内側
他方が 円の 外側
になる
円の 中心座標の 領域を
求めよ
円の 方程式は これなんだって
そこで
39
f(x、y)= にすれば
で
2点を代入したものが
領域の 外と 内 なので
積が マイナス
40
これを 計算すると
41
二つの 積が マイナス
42
ところで
ここでいうところの
a,bは
それぞれ
円の 中心の
x座標 y座標
であるので
x、y を a,bに 代入して
今までのように
領域を
場合分けして
求めると
43
それぞれ
こんなだから
44
こんな感じに なるんだって
お疲れ様です。