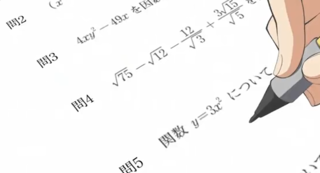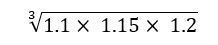航空ロールアウト

関数電卓で数検（実用数学技能検定）の問題を解いてみる。
（ちなみに、実際の検定試験では電卓は使用できない。単に関数電卓を使ってみるだけである。）

問題は公式HPから拝借した。

1級の問題である。

問題1：

2018n≣2(mod 1000)を満たす正の整数nの最小値を求めなさい。

方程式であるのでSOLBER（ソルバー）機能にて解く。
だか、しかし。解くことができない。
MOD（割り算の余り）を使用するためである。
関数電卓で余りのみを求めることはできずに、商と余りの両方セットでの結果となる。
答えが１変数になる関数でないとソルバ機能の式としては使用できない。


問題2：

tan( 2Arctan(1/3) + Arctan(1/12) )の値を求めなさい。ただし、Arctan x はtan x の逆関数を表し,-π/2＜Arctan x＜π/2とします。

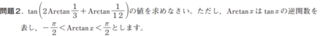
関数電卓に式通りに入力すれば回答が得られる。
使用する関数は、tan、Arctanである。
なお、問題文にも説明があるように、Arctanとは、アークタンジェントであり、tanの-1乗（tan^-1）である。