今日は、中3会員が、期末テストの範囲になっている2次関数(yがxの2乗に比例する関数)の応用問題に取り組んでくれました♪
<こんな問題でした>
【問題】
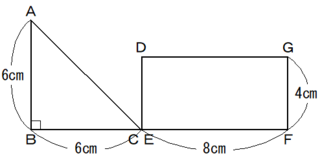
下の図のような直角二等辺三角形ABCと長方形DEFGがあり、直角二等辺三角形の頂点Cが長方形DEFGの辺EF上を点EからFまで秒速1cmで動きます。x秒後の2つの図形の重なった部分の面積をyc㎡とするとき、次の問いに答えなさい。
(1) 0≦x≦4 のとき、yをxの式で表しなさい。
(2) 4≦x≦6 のとき、yをxの式で表しなさい。
(3) 0≦x≦8 のときのyの変化をグラフに表しなさい。
<制限時間10分>
【思考の順番】
(1) 0≦x≦4 のとき、重なった部分の形は直角二等辺三角形になる。点Cは毎秒1cmで進むので、x秒後のDC=xcm、高さもxcmだから…。
(2) 4≦x≦6 のとき、重なった部分の形は台形になる。下底=xcm、高さ=4cmだけど、上底は???
(3) (1)(2)から0≦x≦6 の範囲のグラフが書けます。問題は 6≦x≦8 のときの面積です。x=7くらいの様子を書いてみるとイメージしやすい!
【答え】
(1) y=1/2x∧2
(2) y=4xー8
(3) 下図
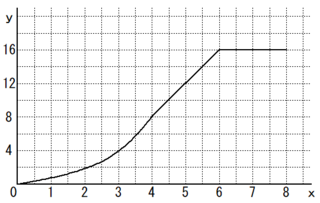
<ポイント>
点の移動と面積の問題は、底辺と高さが同時に変化するときは2次関数、どちらか一方が変化するときは1次関数、どちらも変化しないときは横一直線のグラフになります。
ということで、受験生は志望校合格に向けて1つでも2つでも「わかる」を積み上げていきましょう!
冬休みからでもお手伝いできます ^∀^b
スタップ首藤
【このカテゴリーの最新記事】