(1)考査問題
構造設計
(選択理由記述式4肢択ー問題)
[ No.1 ]
図1のように一様断面の完全弾塑性体の連続梁があり、A点は固定、B点はピンローラー支持されている。C点にαP、D点にPの鉛直下向きの荷重が作用している。Pを漸増させていくと、αの大きさによって、図2に示す機構a、または図3に示す機構bの崩壊機構が形成さる。これらの図中のPuは崩壊機構が形成されるときのPである。次の記述のうち、誤っているものを1つ選び、誤りとする理由を述べよ。なお、αは正(+)の係数、梁の全塑性モーメントはMpとする。
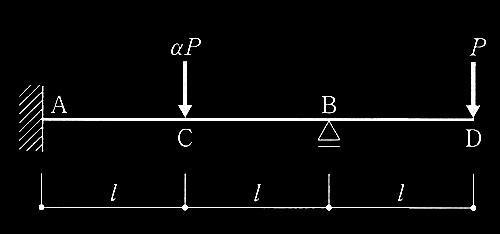
図1
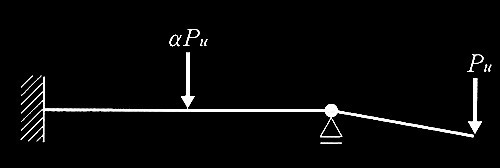
図2 機構a
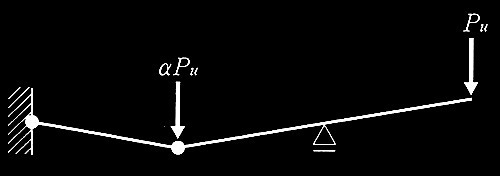
図3 機構b
1. 機構aのPuは、Mp/ℓである。
2. B点の曲げモーメントの値は、αに関係なくPℓである。
3. 機構bのPuは、3Mp/|(α - 1)ℓ|である。
4. α = 2 のときの崩壊機構は、機構bである。
答え
4
[ 解答解説 ]
1.記述の通り。
機構aのヒンジ発生点Bの曲げモーメントはPuで表すとMp=Pu × ℓから、Pu = Mp/ℓとなる。
2.記述の通り。
B−D間は片持ち梁であり、B点の曲げモーメントは必ずPℓとなる。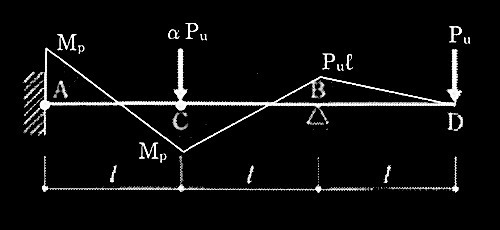
3.記述の通り。
せん断力の釣合いから方程式を求める。
機構bではA点とC点はヒンジであるので、AC間のせん断力はQu=2Mp/ℓ
BC間のせん断力は (Mp + Puℓ)/ℓ で、この合計がC点の外力と釣合うので
2Mp/ℓ + (Mp + Puℓ)/ℓ= αPu
よって、
Pu = 3Mp/{ (α-1) ℓ}
となる。
4.
α=2のときの機構bとなるPuは3Mp/ℓであり、機構aとなるPuのM/ℓより大きい。故に、破壊機構はaとなる。
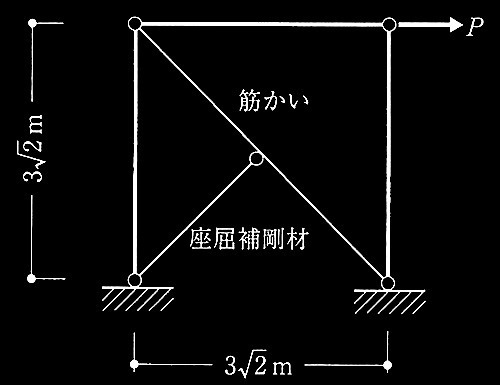
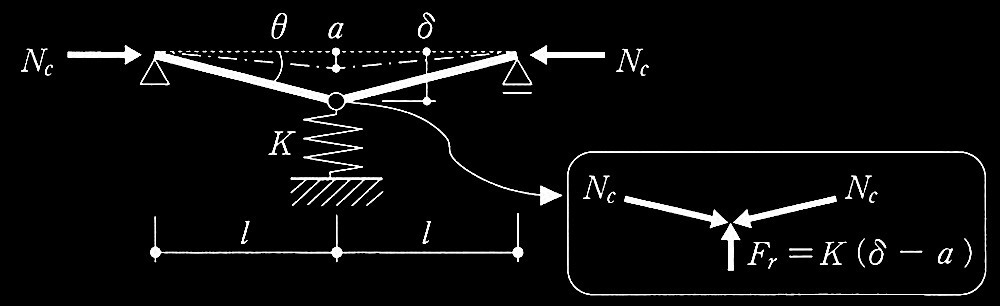
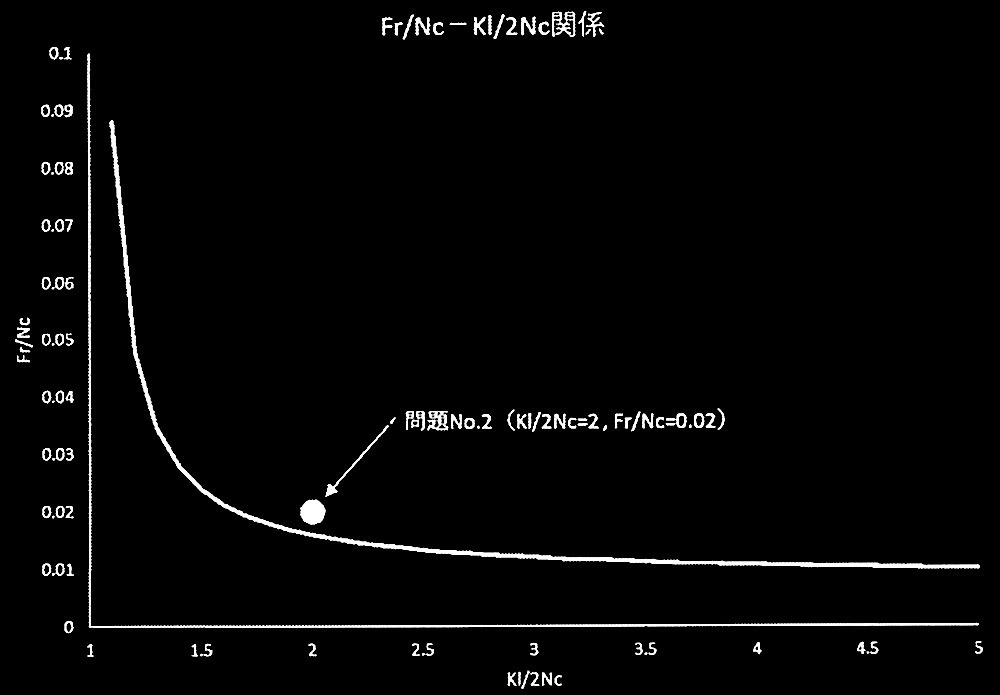
[ No.2 ]
鉄筋コンクリート造に関する次の記述のうち、最も不適当なものを選び、不適当とする理由を述べよ。
1. 床スラブの長期たわみは、両辺固定の場合、弾性計算によって得られる値のおよそ12〜18倍となる。
2. すべての層のDsが0.3となる鉄筋コンクリート造建築物の大地震時の最大応答層間変形角は、荷重増分解析における必要保有水平耐力時の層間変形角と同等である。
3. 連層耐力壁の地震時の変形は、低層建築物では曲げ変形よりせん断変形の占める割合が大きく、高層建築物では曲げ変形の占める割合が大きくなる。
4. 鉄筋コンクリート造の柱では、鉛直荷重によってコンクリートに圧縮クリープが生じ、コンクリートの圧縮応力が徐々に減少していく。
答え
2
[ 解答解説 ]
1.記述の通り。
(テキスト第II編第3章8-3たわみ 長期たわみP. 354)
2.Dsの値によらず(架構形式によらず)保有水平耐力計算における増分解析の結果は、保有水平耐力時、必要保有水平耐力時ともに架構の最大応答変形とは必ずしも一致しない。よって誤り。
(テキスト第II編第2章2-2耐震設計法P. 179)
3.記述の通り。
4.記述の通り。
テキストには鉄筋の圧縮のところに「コンクリートの収縮ひずみとクリープひずみ分を考慮しても降伏ひずみを超えないように設定されている」という記述があり、鉄筋の圧縮応力が増加することが示されている。
(テキスト第II編第3章3-2鉄筋の材料特性P.275)
[ No.3 ]
構造計画•構造解析に関する次の記述のうち、最も不適当なものを選び、不適当とする理由を述べよ。
1. べた基礎の設計における基礎梁の設計用荷重は、建築物自重によって地盤に作用する接地圧から最下柱脚より下部の基礎躯体重最を差し引いた分を地反力とした上向きの鉛直荷重としてよい。
2. 鉄骨造の建築物において、1階を無柱空間とするために2階の設備階を1層分の鉄骨トラス梁として設計する場合には、建築物のすべての階の床を剛床と仮定して構造解析を行ってよい。
3. 構造計画にあたっては、建築物の建設地域や規模により使用できる施工技術が異なるため、施工性についても考慮する必要がある。
4. 大きなスパンに曲げ剛性が十分に大きい中空スラブを用いる場合、スラブの支持条件は、周辺固定とするのではなく周辺大梁のねじり剛性を考慮して設定し、スラブの応力計算を行う必要がある。
答え
2
[ 解答解説 ]
1.記述の通り。
2.上下階の梁はトラスの弦材となるため軸変形を考慮しなければならない。剛床とした場合、軸変形が拘束され鉛直変位が過小評価となるため、不適当。
(テキスト第 Ⅰ 編第4章3.2トラス梁のモデル化と剛床仮定P. 84)
3.記述の通り。
(テキスト第II編第1章3-2与条件の把握と整理P. 139)
4. 記述の通り。
(テキスト第II編第3章8-2床スラブP. 353)
[ No.4 ]
耐震設計に関する次の記述のうち、最も不適当なものを選び、不適当とする理由を述べよ。
1. 限界耐力計算では、極めて稀に発生する地震による加速度によって建築物の各階に作用する地震力を計算し、当該地震力が保有水平耐力を超えないことを確かめる。
2. エネルギーの釣合いに基づく耐震計算では、極めて稀に発生する地震に対して各階の主架構の保有エネルギー吸収量と必要エネルギー吸収量を比較し、安全性を検討する。
3. 保有水平耐力計算では、保有水平耐力を計算する対象の崩壊形には、全体崩壊形や部分崩壊形のほかに、局部崩壊形がある。
4. 許容応力度計算では、作用荷重により部材に生じる応力を線形解析により算定して、部材の断面に生じる最大応力度が材料強度以下であることを確認する。
答え
4
[ 解答解説 ]
1.記述の通り。
限界耐力計算は、地震動の要求スペクトル(各階に生じる地震力)と構造物の耐カスペクトル(保有水平耐力)を比較して、耐震安全性を検討する方法で、地震力と保有水平耐力の定義は施行令第82条の5の五に記載されている。
(テキスト第II編第2章2-2耐震設計法P. 179)
2.記述の通り。
(テキスト第II編第2章2-2耐震設計法P. 184)
3.記述の通り。
(テキスト第II編第2章2-2耐震設計法P. 177)
4.最大応力度が許容応力度以下であることを確認する。
(テキスト第II編第2章2-2耐震設計法P. 176)
[ No.5 ]
鉄骨構造に関する次の記述のうち、最も不適当なものを選び、不適当とする理由を述べよ。
1. 鋼材の応カーひずみ関係では、鋼材強度が高くなると、一様伸び(引張強さに対応するひずみ)と破断伸びは、ともに低下する。
2. 鋼材の強度は、一般に、ひずみ速度依存性があり、ひずみ速度が速くなると降伏点が低下する。
3. 構造部材の接合部を高カボルト接合と溶接接合の併用継手とする場合、高カボルトを締め付けた後に溶接を行う場合には、それぞれの許容耐力の和をその接合部の許容耐力とすることができる。
4. 伸び能力のあるアンカーボルトの降伏により終局耐力が決定される露出柱脚の履歴特性は、スリップ型の性状を示す。
答え
2
[ 解答解説 ]
1.記述の通り。
(テキスト第II編第3章2-1鋼材の特性P. 251)
2.ひずみ速度が速くなると強度は増大するため、不適当。
(テキスト第II編 第3章2-1鋼材の特性P. 252)
3.記述の通り。
4.記述の通り。
[ No.6 ]
鉄筋コンクリート造の構造設計に関する次の記述のうち、最も不適当なものを選び、不適当とする理由を述べよ。
1. 柱部材の材端部の横補強筋量を増すと、圧縮側のコアコンクリートを拘束する効果があるので、曲げ破壊後の塑性変形性能が向上する。
2. コンクリートのヤング係数は、ほぼ圧縮強度の立方根に比例するので、構造解析における部材剛性の算定では、設計基準強度に対応したヤング係数を用いる。
3. 柱及び梁部材の付着割裂強度は、横補強筋の降伏点が大きいほど上昇する。
4. 圧縮軸力と曲げモーメントを同時に受ける柱において、中立軸が柱断面の外に出る場合は、曲げひび割れは発生しない。
答え
3
[ 解答解説 ]
1.記述の通り。
(テキスト第II編第3章3-8部材の変形性能P.287)
2.記述の通り。
(テキスト第II編第1章2-2鉄筋コンクリートP. 131)
3.テキストには直接的な記載はないが、日本建築学会「鉄筋コンクリート構造計算規準 同解説 2018」の付着応力度の検討に用いる横補強筋のパラメータは、全断面積と間隔のみで降伏点は関係がないため不適当。テキストには付着長さの減少に伴う付着割裂破壊の説明の記述がある。(テキスト第II編第3章3-8部材の変形性能P. 286)
4.記述の通り。
中立軸が柱断面の外に出る場合は、全断面が圧縮領域にあるということである。
[ No.7 ]
木質構造の構造設計等に関する次の記述のうち、最も不適当なものを選び、不適当とする理由を述べよ。
1. 一般に、木材の圧縮、引張、曲げの基準強度は、圧縮が最も大きく、引張が最も小さい。
2. 面材耐力壁の許容せん断耐力は、①降伏耐力Py、②終局耐力と靭性を考慮した特性値、③最大耐力Pmaxの2/3、④1/200rad時等の特定変形角時の耐力、のうち最小値から求めることとしている。
3. 低層小規模建築物の偏心率の計算には、壁の剛性を評価する指標として、耐力の指標である壁倍率を用いることが多い。
4. 鋼材板挿入ドリフトピン接合の耐力算定で、木材の繊維の方向と力の方向が異なる場合には、ハンキンソン式により降伏耐力を求める。
答え
1
[ 解答解説 ]
1.木材の基準強度は曲げが最大であり、不適当。
(テキスト第11編第1章2-3木材P. 135)
2.記述の通り。
記述の内容は耐力壁の許容せん断耐力の算定方法の内、実験による方法について記述したもの。その他に、大臣認定を受けた壁倍率を許容耐力に換算する方法と、面材とくぎのすべり特性の関係から算出する方法がある。
(テキスト第11編第3章1-3鉛直架構のモデル化と靭性P. 232)
3.記述の通り。
(テキスト第11編第3章1-4共通事項P. 243)
4.記述の通り。
(テキスト第11編第3章1-4共通事項P. 240、247)
[ No.8 ]
免震構造•制振構造に関する次の記述のうち、最も不適当なものを選び、不適当とする理由を述べよ。
1. 免震部材の機能には、支承機能、減衰機能、復元機能があり、弾性すべり支承は支承機能のほか減衰機能を有するが、転がり支承は摩擦係数が非常に小さいので減衰機能はほとんどない。
2. 弾塑性ダンパーを用いた免裳構造においては、ダンパーの数を増やすほど応答加速度の低減効果が高まるわけではない。
3. 弾塑性ダンパーを配置した制振構造においては、ダンパーを付加する前の水平剛性が大きい骨組より、水平剛性が小さい骨組のほうが、ダンパーによる応答加速度の低減効果は大きい。
4. 粘性ダンパーを配置した制振構造においては、ダンパーの数を増やすほど、応答変位及び応答加速度は小さくなる。
答え
4
[ 解答解説 ]
1.テキストの転がり支承の記述には、一定の低摩擦係数の特性を有するとなっているが、実際の転がり支承の摩擦係数は非常に小さく、減衰機能はほとんどないため、記述の通り。
「(テキスト第II編第3章6-1免震構造 P.321)
2.記述の通り。テキストの免震構造の部分にはこのような記載はないが、4の制振構造の記述にもあるようにダンパーの付加によって固有周期が短くなり、応答化速度はかえって増加するという現象が免震構造でも起こるため。
(テキスト第II編第3章6-2制振構造P. 328)
3.記述の通り。
(テキスト第II編第3章6-2制振構造P. 325)
4.ダンパーを付加することでダンパー付加剛性により固有周期が短くなるため、付加するダンパー量が多すぎると、加速度応答はかえって増加してしまう。そのため最も不適当。(テキスト第II編第3章6-2制振構造P.328)
[ No.9 ]
地盤•基礎に関する次の記述のうち、最も不適当なものを選び、不適当とする理由を述べよ。
1. 標準貫入試験を実施すると地盤のN値が求められるだけでなく、同時に採取した試料を分析して、液状化判定に必要な粒度分布などの物理特性を求めることができる。
2. 粘性土のせん断強さを求める室内試験のうち、サンプリングによる試料の乱れの影響を小さくするために行う3軸圧縮試験(非圧密非排水試験(UU試験))では、内部摩擦角(せん断抵抗角)と粘着力が得られるが、基本的には内部摩擦角は無視し粘着力のみを評価して設計に用いる。
3. 地盤改良工法の一つに振動締固め工法があるが、この工法は軟弱な粘性土を含む地盤に対して強度及び剛性を増大させる効果がある。
4. 一般に液状化の可能性を検討するのは、地表から20m以浅の飽和砂地盤で、細粒分含有率が35%以下、粘土分含有率が10%以下の沖積層または埋立て地盤である。
答え
3
[ 解答解説 ]
1.記述の通り。
(テキスト第II編第3章7-3地盤調査P. 336)
2.記述の通り。
(テキスト第II編第3章7-2地盤に関する基礎知識P. 334)
3.締固めは、主に緩い砂質地盤に対して行うものであり、最も不適当。
(テキスト第II編第3章7-4基礎構造計画P.340)
4.テキストにあるように、液状化判定の対象とすべき地盤の条件には、「沖積層または埋め立て地盤」という言葉はなくなっているが、より不適当な記述があるのでそちらが回答と考える。
(テキスト第II編第3章7-2地盤に関する基礎知識P. 333)
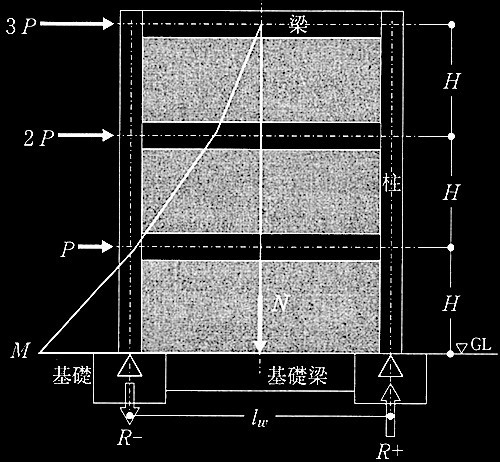
[ No.10 ]
建築物の耐震診断・耐震補強に関する次の記述のうち、最も不適当なものを選び、不適当とする理由を述べよ。
1. 「既存鉄筋コンクリート造建築物の耐震診断基準 同解説(2017年改訂版)」の第1次診断用靭性指標Fを求めるときの極脆性柱とは、柱内のり寸法(ho)と柱せい(D)の比(ho/D)が2以上の独立柱をいう。
2. 既存鉄筋コンクリート造建築物の現地調査によるコンクリートコアの圧縮強度の平均値が 13.5 N/mm2を下回り、かつ設計基準強度の3/4以下の場合は、材料や施工等に問題があると考えられるため、改築も視野に入れた総合的な検討が必要になる。
3. 体育館、公民館、工場など大スパン架構の既存鉄骨造建築物の耐震診断において、屋根面で十分に荷重伝達ができない場合には、適宜、平面骨組に分け、構面単位で構造耐震指標 Isi 及び保有水平耐力に係る指標 qiを評価するなど、荷重伝達と各部の挙動を考慮した検討が必要になる。
4. 木造住宅の精密診断法の一つである保有耐力診断法では、耐力要素の耐力を累加し、それに「剛性率による低減係数」及び「偏心率と床の仕様による低減係数」を乗じて、上部構造の保有する耐力を算定することとしている。
答え
1
[ 解答解説 ]
1.不適当。
記載の定義は「極短柱」のことであり、「極脆性柱」はその中でもせん断破壊が曲げ破壊より先行するもののことである。
2.記述の通り。
3.記述の通り。
(テキスト第1I編第4章3-2耐震性の判定P. 387)
4.記述の通り。
(テキスト第1I編第4章4-3精密診断法P. 390)