問題3
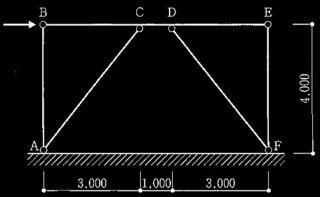
図1に示すような、1層の鉄筋コンクリート造平面架構を考える。図のように梁BCの中心軸に沿って、水平方向に荷重Pを加えたところ、図1に示すように梁の両端と両柱の柱脚に降伏ヒンジが生じた。なお、梁の降伏位置は図1に示す通り柱面、柱の降伏位置は柱底面であるとする。また、梁の終局モーメントは108kN•mである。柱の終局モーメントMuと作用している軸力Nの間には、図2及び式(1) に示すような相関関係がある。コンクリートの設計基準強度は18N/mm2、梁の有効せいdは断面せいDに対して d = 0.9D、柱の引張鉄筋比ptは 0.7%、地震地域係数Z、振動特性係数Rt、及び形状係数Fesはすべて1.0とする。また、柱•梁部材はともに、せん断破壊等の脆性的な破壊に対しては十分な安全率を有しているものとする。次の[ No.1 ]~[ No.3 ]の設問について解答せよ。
く平面架構の諸元>
柱:600 mm × 600 mm
梁:梁幅B 300mm × 断面せいD 500mm
屋上階の重量:360kN(その他の部分の重さは無視する)
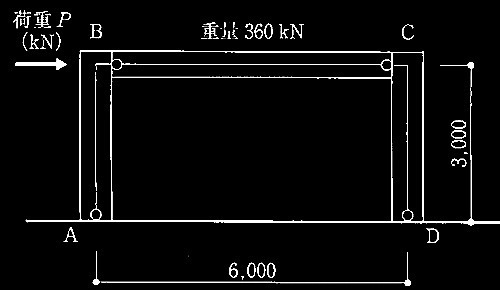
図1 平面架構(単位:mm)
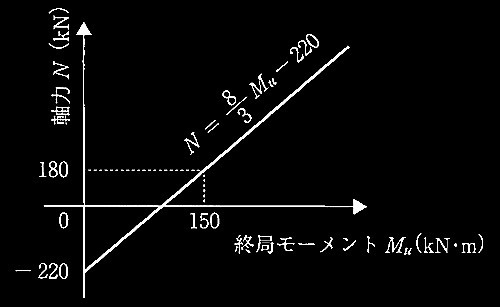
図2 柱の終局モーメントMuと軸力Nの関係
[ No.1 ]
次の記述の空欄 [ ① ] ~ [ ⑧ ] に入る数値を記入せよ。
荷重Pが作用することによりすべての降伏ヒンジが形成されて崩壊メカニズムが形成されたとき、柱ABには引張方向に、柱DCには圧縮方向に変動軸力 N = [ ① ] kNが作用する。柱AB及び柱DC に作用している軸力はそれぞれ、NAB = [ ② ] kN、NDC = [ ③ ] kNとなる。図2及び式(1)より、柱AB及び柱DCの終局モーメントMu はそれぞれ、MuAB [ ④ ] 、MuDC = [ ⑤ ] kN•mとなる。よって、崩壊メカニズム時に柱AB及び柱DCが負担する水平力はそれぞれ、PAB = [ ⑥ ] kN、PDC = [ ⑦ ] kNとなり、この架構の保有水平耐力Qu = [ ⑧ ] kNとなる。
答え
[ 解答解説 ]
梁が終局曲げモーメントに達した際の応力概念図を以下に示す。
なお、以降の計算において、軸力は圧縮側を正とする。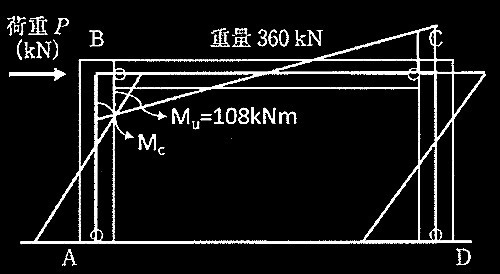
梁の終局曲げモーメントMuは問題文より108kNmであり、これが柱フェイス位置で作用するものと考えると、柱内法スパンは6m – 0.6m = 5.4mであることから、大梁のせん断力は以下となる。
QGu = 108 × 2 / 5.4 = 40kN
このせん断力が柱に対する変動軸力となるので、
① NE = 40kN
柱の長期軸力NLは重量が360kNであることから、
NL = 360 / 2 =180kN
よって柱AB及び柱DCに作用する軸力は以下のようになる。
②NAB = 180 – 40 = 140kN
③NDC = 180 + 40 = 220kN
柱の終局曲げモーメントは式(1)をMuについて展開すると、以下のように求められる。
④柱AB : MuAB = 3/8 × (NAB + 220) = 135kNm
⑤柱DC : MuDC = 3/8 ×(NDC + 220) = 165kNm
柱頭部の梁芯位置における曲げモーメントは柱AB,柱DC共に、
Mc = Mu + QGu × 0.3m
= 108 + 40 × 0.3
= 120kNm
柱脚部の曲げモーメントは前述の④、⑤となるので、柱AB及び柱DCに作用する水平力は、即ち柱のせん断力となるため、
⑥ 柱AB : PAB = (120 + 135) / 3.0 = 85kN
⑦ 柱DC : PDC = (120 + 165) / 3.0 = 95kN
(せん断力算出用の階高を梁芯からとしている点に注意)
よって、この架構の保有水平耐力は、
⑧Qu = 85 + 95 = 180kN
となる。
[ No.2 ]
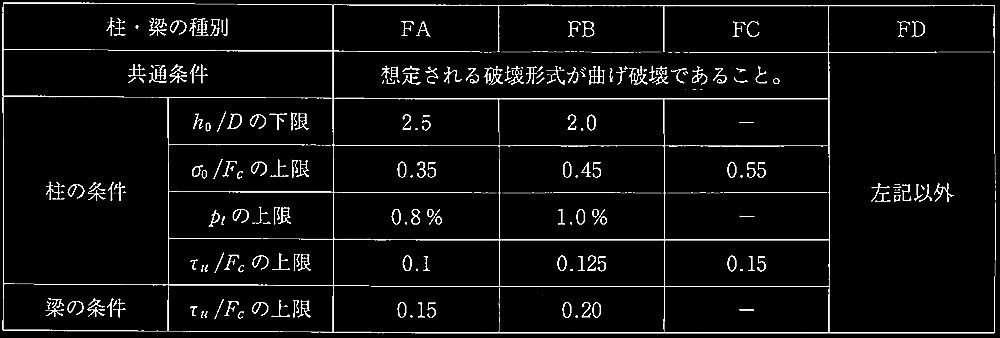
この架構の必要保有水平耐力Qunを求めよ。なお、部材種別判定は表2に従う。ただし、τuの計算において長期荷重によるせん断応力は無視してよい。また、構造特性係数Dsは、柱・梁の部材群の種別に応じて、A:0.30、B:0.35、C:0.40、D:0.45である。
表2 部材種別判定表
答え
[ 解答解説 ]
柱及び梁の部材ランクを判定する。
柱について
ho/D = (3000 –250) / 600 = 4.58
σo/Fc = (220000 / 6002) /18 = 0.0340
Pt = 0.7%
τu/Fc = (95000/6002)/18 = 0.0147 < 0.10
以上より、柱はFAランク
梁について
τu/Fc = (40000/300/500)/18 = 0.0148 < 0.15
以上より、梁はFAランク
以上より架構のランクはFAとなり、構造特性係数Ds = 0.30となる。
よって必要保有水平耐力Qunは以下のようになる。
Qun = Z•Rt•Ai•Co•Ds•Fes•W
= 1.0 × 1.0 × 1.0 × 1.0 × 0.30 × 1.0 × 360
= 108kN
[ No.3 ]
ptが小さい柱の場合、破壊形式は曲げ破壊が先行し、部材は表2のFA又はFBに分類される。しかし、ptが大きくなると部材が表2のFDに分類されるような破壊形式になる。ptの上限はこの破壊形式の防止を目的として規定されている。その破壊形式とその力学的特徴を簡潔に記述せよ。
答え
[ 解答解説 ]
黄色本 P395 「6.4.4(2) 鉄筋コンクリート造の構造特性係数Dsの算出方法」 参照
c)柱のせん断力に起因するもう一つの脆性破壊の形式として,異形鉄筋を主筋とする柱の付着割裂破壊がある。一般に鉄筋コンクリート造部材の曲げ補強筋として用いられる異形鉄筋とコンクリートとの付着性能は非常によく,鉄筋がコンクリートから抜け出すことはまずない。しかしながら,抜け出さない代わりに,鉄筋周囲のコンクリートを局部的に破壊し,結果的に抜出しと同じくコンクリートと鉄筋がばらばらになる状態に至る。これを付着割裂破壊と呼ぶが、この破壊形式は抜出しとは異なり,引張側のかぶりコンクリート部分が剥落するので逆向きの曲げ応力の下では部材せいの減少による耐力低下も生じる。
この破壊形式は、引張鉄筋の存在応力の材長方向の変化が大きい時,すなわち,曲げ応力とせん断力とがともに大きい時に, 1本の引張鉄筋に対するコンクリート断面の幅が小さい部材で生じる。具体的には,引張側で多数の鉄筋が一列に並ぶ部材で引張側のかぶりコンクリートが
【破壊形式】
付着割裂破壊
【力学的特徴】
引張鉄筋の存在応力の材長方向の変化が大きい時、即ち、曲げ応力とせん断力とがともに大きい時に、1本の引張鉄筋に対するコンクリート断面の幅が小さい部材で生じる。鉄筋周囲のコンクリートを局部的に破壊し、コンクリートと鉄筋がばらばらになる破壊状態となる。