2024�N08��28��
�ߘa�O�N�x�C���l�� �\���v�i�L�q���j���P
���P
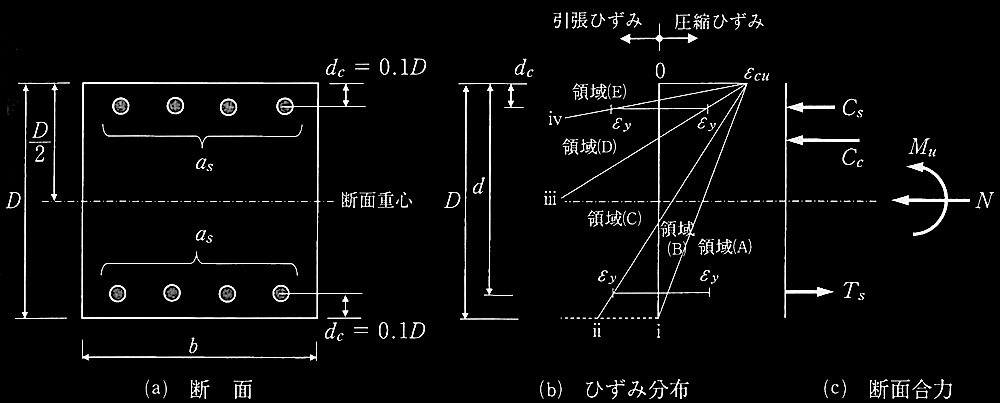
�}1(a)�Ɏ����A�����`�f�ʂ����S�R���N���[�g�������A�f�ʏd�S�ʒu�ɍ�p�����莲��N�i���k�𐳂Ƃ���j�̉��ŏI�NjȂ����[�����gMu�ɒB����ꍇ���l����B�I�NjȂ����[�����gMu�́A�}1 (b)�̂Ђ��ݕ��z�Ɏ����悤�ɁA�R���N���[�g���k���Ђ��݂��I�ǂЂ��� ��cu�ɒB�����Ƃ��̒f�ʏd�S���̃��[�����g�Ƃ���B�Ђ��ݕ��z�Ƃ��Ď��͂̑傫���ɉ������T�^�I�ȕ��z i �`iv���l���A�����̂Ђ��ݕ��z�Ԃ̗̈���A���ꂼ��̈� (A)�`(E)�Ƃ���B�f�ʂɂ͕��ʕێ��̉��肪�������A�R���N���[�g�͈������͂S���Ȃ����̂Ƃ���B���k�R���N���[�g�̉��͂́A�}2�Ɏ����������k���̓u���b�N��p����B�Ȃ��A�S�̉��J�[�Ђ��݊W�͊��S�e�Y���̃o�C���j�A�`�Ƃ���B�}3�ɁA�f�ʂ�N-Mu���ݍ�p�}�������B�}���ɂ͂Ђ��ݕ��z i �`iv�A�y�т��̊Ԃ̗̈�iA)�`(E)�������B
�ȉ���[ No.1 ]�`[ No.3 ]�̐ݖ�ɉ���B
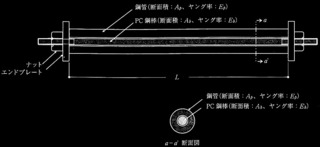
�}1 ��莲�͂̉��ŋȂ��I�Ǐ�ԂɒB���钌
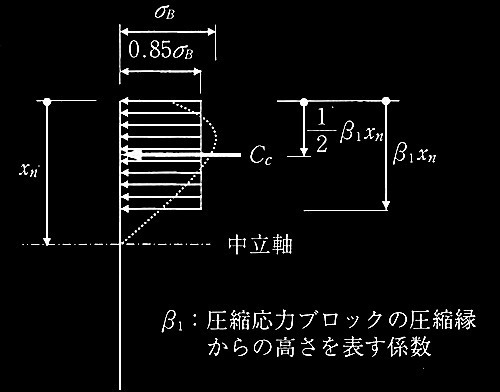
�}2 �R���N���[�g�̓������k���J�u���b�N
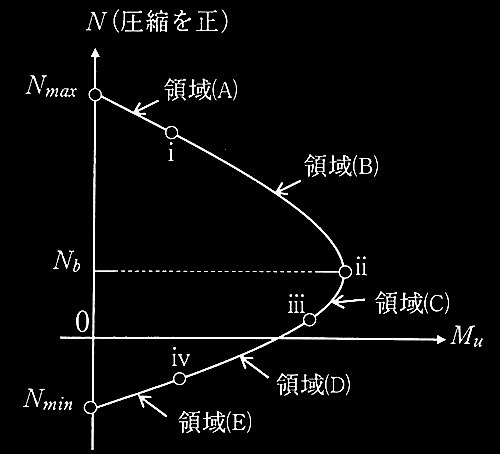
�}3 �f�ʂ�N-Mu���ݍ�p�}
�y�L���ꗗ�z
b�F���f�ʂ̕�
D�F���f�ʂ̑S����
as�F���k�S�A�����S���ꂼ��̒f�ʐ�
dc�F���k���܂��͈��������爳�k�S�܂��͈����S�ؒ��S�܂ł̋����� dc = 0.1D
d�F���k����������S�ؒ��S�܂ł̋����i�L�������jd = 0.9D
��B�F�R���N���[�g�̈��k���x
��y�F�S�̍~���_
��cu�F�R���N���[�g�̋Ȃ����k���Ђ���
��y�F�S�̍~���Ђ���
Cc�F�R���N���[�g�̈��k���́i���k�𐳁j
Cs�F���k�S�̈��k���́i���k�𐳁j
Ts�F�����S�̈������́i�����𐳁j
xn�F���k�����璆�����܂ł̋����i�������[���j
[ No.1 ]
���L�̇@�`�D�̏�Ԃ́A���ꂼ��}l(b)�y�ѐ}3�ŕ\�����̈�(A)�`�̈�(E)�̂ǂ̗̈�ɑ������邩��I�сA���ɗ̈�̋L��(A�`E)���L������B
�@ �����S�����k�S�������~�����Ă����ԁB
�A �����S�͈����~�����Ă��āA���k�S�͈��k�~�����Ă����ԁB
�B �����S�͈����~�����Ă��āA���k�S�͒e���͈͂̏�ԁB
�C �S�f�ʂ����k�̏�ԁB�������͒f�ʊO�ɂ��舳�k���J�u���b�N�͓K�p�ł��Ȃ��B
�D �����S�͒e���͈͂ŁA���k�S�͈��k�~�����Ă����ԁB
����
[ ��� ]
�@�����S�����k�S�������~���i�����̈�j�ɂ��邱�Ƃ���A�̈�E
�A�����S�̓�y�ɓ��B���A���k�S����y�ɓ��B���邱�Ƃ���A�̈�C
�B�����S�̓�y�ɓ��B���邪�A���k�S�͒e���͈͂Ń�y�ɓ��B���Ȃ��̂ŁA�̈�D
�C�S�f�ʂ����k�̈�Ȃ̂ŁA�̈�A
�D�����S�͒e���͈͂Ń�y�Ɏ��炸�A���k�S����y�ɓ��B���邱�Ƃ���A�̈�B
[ No.2 ]
���͂��}3�̎���Nb�i���k�𐳁j�̂Ƃ��A�I�NjȂ����[�����gMu�����߂�ȉ��̋L�q�ɂ� ���āA�@�`�I�ɓ���K�Ȏ��܂��͗p����A���̐ݖ▖���̑I�����i���j�`�i�Ёj�̒�����I��ŁA���ɂ��̋L���i�Ђ炪�ȁj���L������B�������A�����L������I�����Ă��悢�B
���͂�Nb�̂Ƃ��A�Ђ��ݕ��z�� (ii)�ƂȂ�B�e���͂̑傫���́ACc = [�@�@�@]�ACs �� [�@�A�@]�ATs= [�@�B�@]�ł���B�Ђ��ݕ��z���^�����Ă���̂ŁA�������[��xn�͊w�I�ɋ��߂邱�Ƃ��ł���B
xn����cu�A��y�y��d�ŕ\���ƁAxn = [�@�C�@]�ƂȂ�B����Nb�́A���� xn ��p���āA���L�̎������J�̒ލ��������狁�߂邱�Ƃ��ł���B
Nb = Cs �| Ts + Cc
�@ = [�@�D�@]�ƂȂ�B
�f�ʏd�S�Ɋւ���Mu�́A�ȉ��̂悤�ɋ��߂邱�Ƃ��ł���B
Mu = Cs �E(D/2 �| dc ) + Ts• (d �| D/2) + Cc•(D/2 �| ��1xn/2)
�@ = [�@�E�@] + Cc•(D/2 �| ��1xn/2)
�����ŁACc•(D/2 �| ��1xn/2)��Nb���܂ގ��Ƃ���[�@�F�@] �ŕ\�����B
����ꂽ�I�NjȂ����[�����g�́A�E���S�ɂ��Ȃ���R�A�F�����͂ɂ��Ȃ���R��\���Ă���B
����Nb�͒��f�ʂ̋Ȃ��j������E���鎲�͂ŁA[�@�G�@]�ƌĂ�Ă���B
���͂�Nb���傫���ꍇ�́A[�@�H�@] �� [�@�I�@] ���ۂ��N��Ȃ��Ȃ�B

����
[ ��� ]
�@�R���N���[�g�̈��k��
�@Cc = 0.85��B × ��1xn × b = 0.85��1��Bbxn �E�E�E(��)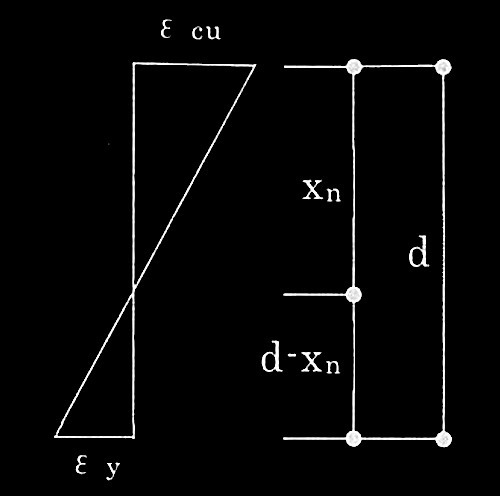
�A ���k�S�̍���
�@Cs = as��y �E�E�E(��)
�B�����S�̍���
�@Ts = as��y �E�E�E(��)
�C �������[��xn
�@��cu : ��y = xn : d – xn ���A
�@��y•xn = ��cu•(d – xn)
�@(��cu + ��y)•xn = ��cu•d
�@xn = ��cu/(��cu + ��y)•d�E�E�E(��)
�D Nb= Cs – Ts + Cc
= 0.85��1��Bbxn = 0.85��1��Bb•��cu/(��cu + ��y)•d �E�E�E(��)
�i�� Ts = Cc = as��y�j
�E Cs•(D/2 – dc) +Ts• (d – D/2) = as��y • (D/2 – dc + d – D/2) = as��y• (d – dc)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@= 0.8as��yD �E�E�E(��)
( �� d = D – dc���d – dc = D – 2dc = 0.8D)
�F �D���Cs = Ts����Nb= Cc�Ȃ̂ŁA
Nb•(D/2 – ��1xn/2) = Nb/2�E(D –��1•Nb/0.85��1��Bb)
�@�@�@�@�@�@�@�@= NbD/2•(1 – Nb/0.85��BbD) �E�E�E(��)
�G ����Nb�́A(��)�ލ������ƌĂ��B
�H�C�I ���͂�Nb���傫���ꍇ�́A�f�ʂ̈��k���x�z�I�ƂȂ�A(��)�����S����(��)�����~�����ۂ��N����Ȃ��Ȃ�B
[ No.3 ]
�}4�͓��f�ʂŁA���͔�i��p���͂̒f�ʈ��k�ϗ͂ɑ����j�݂̂��قȂ�S�R���N���[�g�����̒f�ʂ̃��[�����g�Ƌȗ��̊W��\���Ă���B�ʏ�̎��͈͂̔͂ł���A���͔䂪�傫���ꍇ�́A�ő僂�[�����g�͑傫���Ȃ�A���E�ό`�i��R���[�����g���ő僂�[�����g����95���ɒቺ�����Ƃ��̕ό`�j�͏������Ȃ�B���̗��R�����ꂼ��L�q����B
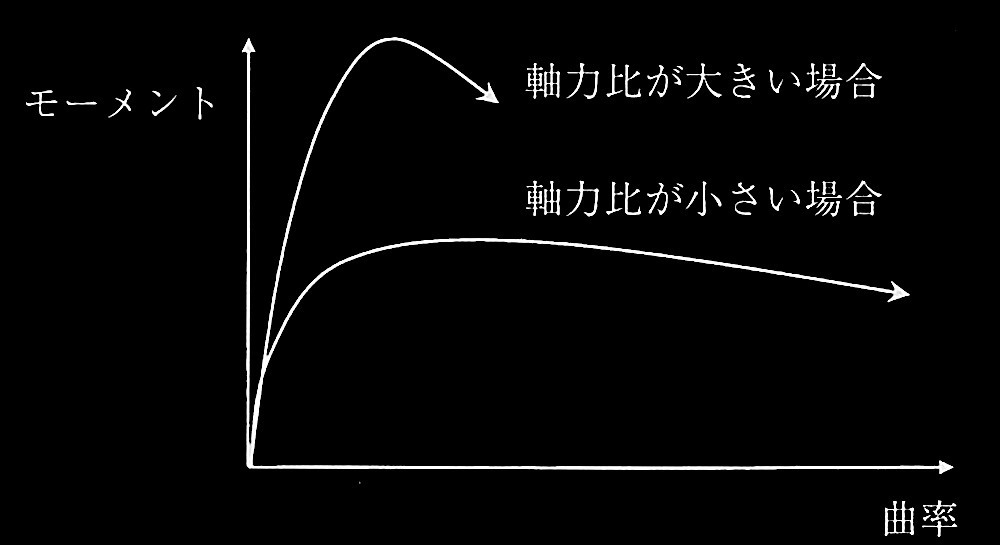
�}4 ���f�ʂ̃��[�����g�Ƌȗ��̊W
����
�ȗ�������RC���f�ʂɂ����āA���͔䂪�傫���ꍇ�́A�R���N���[�g�̕��S���鈳�k���͂̊������傫���Ȃ�B���̌��ʁA�ő僂�[�����g�͑傫���Ȃ�B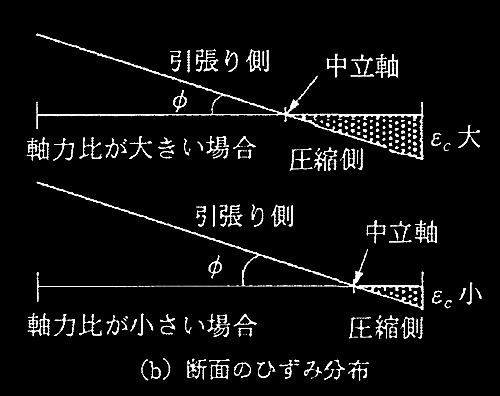
����A���k�����璆�����ʒu�܂ł̋����������A���k���ߖT�ɂ����鈳�k�Ђ��݂��傫���Ȃ�B����āA�R���N���[�g�̍ő�ϗ͈Ȍ�̑ϗ͒ቺ�̉e�����ό`�̑����i�K�Ō����ɂȂ邽�߁A���E�ό`�͏������Ȃ�B
���̋L���ւ̃g���b�N�o�b�NURL
https://fanblogs.jp/tb/12678437
���u���O�I�[�i�[�����F�����g���b�N�o�b�N�̂ݕ\������܂��B