ので、θ の範囲を広げて、f(θ) が点線のように正負にずーっと続く周期関数にしたいのです。そこでまた x - y 座標に戻って、どうすればいいのか考えてみましょう。

　

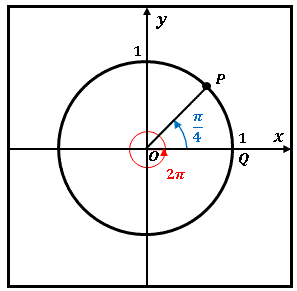
　円周上を動く P と 座標 Q(1, 0) を結ぶ弧長 PQ で θ を定義していましたね。そのままの定義では弧長 PQ は 0 から 2π の範囲しかとれないわけです。そこで上図の赤い線で示したように、P はすでに 1 周 (2π) 動いていて、そのあと 2 周目 に入っているという考え方をしてみます。上図の青い部分は弧長で考えると角度 π/4 ですが、1 周目と合せると

2π + π/4 = 9π/4
の角度であると考えるのです。同じように 2 周目、3 周目 ...... とぐるぐる回せば、θは正方向に全ての実数をとることができるようになります。また負の方向（時計回り）にも同様に 2 周目、3 周目 ...... とぐるぐるさせると、めでたく θ は全実数で定義されるようになります。再び θ を横軸にしたグラフを描くと次のようになります。

　

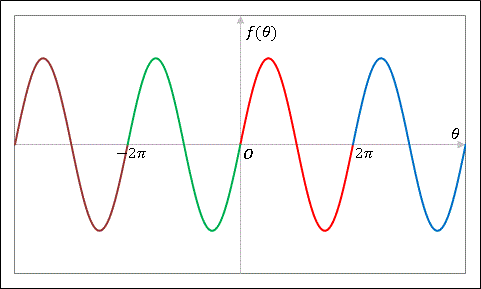
　赤い部分が正方向の 1 周目、青い部分は 2 周目に対応しています。