高校受験・大学受験対策の勉強法で偏差値６０以上

この広告は30日以上更新がないブログに表示されております。
新規記事の投稿を行うことで、非表示にすることが可能です。

受験本番に強くなる勉強法とは？

一瞬で勉強にとりかかれるCDレゾ・メモリー超記憶脳

あなたは、受験本番で

自分の能力を100％発揮したいと思っているかもしれません。


もし、本気でそう思っているなら、

今すぐに普段の勉強法を変えるべきです。



残念ながら、ほとんどの受験生は、

受験本番で１００％の実力を発揮できていない！？


模試の結果を見て、

こんなことを思ったことはありませんか？


「なんでこんなところでミスしたんだろう？」


「落ち着いてやればできるのに・・・」


このようなことを思ったことがある人は

自分の実力を１００％発揮できていないということになります。


本番で８０％くらいの実力が出せれば良い方ではないでしょうか？


８０点位とれるだろうと思っていても

その８０％しか実力が出せないということは、

６４点しかとれないということになります。



なぜ、本番で実力が発揮できないのか？


例えば、

サッカーの日本代表の試合で

ホームとアウェイの違いを考えてみてください。


ホームでは実力を出しやすくて

アウェイでは実力が出にくい

ということをよく聞くと思います。


まさに、

あなたにとってのホームは、家や塾です。

アウェイは、試験会場です。


環境が変わり普通ではいられなくなってしまうので

実力が出ないのです。


また、

普段の勉強法がテスト本番で

ちゃんと実力を発揮できるようになっていなければ

意味がありません。



時間的なプレッシャーをかけてみてください。

少し、ざわついたところで勉強してください。


あなたの普段の勉強する環境と

テスト本番での環境の違いを

徹底的にあぶり出してください。


模試であなたが感じたことを

紙に書き出してみてください。


どんなことを感じていたのか？

どの問題にどのくらいの時間をかけたのか？


自分のことを注意深く観察してみることで

あなたは受験本番で１００％の

実力を発揮できるようになります！


本気なら、今すぐにやるべきです。




この記事を読んだ証拠にコチラをクリックしてください↓

数学科・算数教育 ブログランキングへ

確率ができない人はたいてい場合の数ができません。

かろうじて場合の数ができていたとしても
確率ができない人は基本法則を思い出してください。


スポンサーリンク






そもそも基本法則とは・・・

和の法則と積の法則のたった２つです。

このたった２つの基本法則は
場合の数のはじめの方に少し触れられるだけで
あとは省略されてしまうので意外と理解しても
いつの間にか忘れて感覚的に使ってしまうんです。

感覚的に考えてしまうので
わかったのかわからないのかはっきりしないということです。

わかった気がしてるのにできない人は、
基本法則を意識してみてください。

基本法則を意識するだけで全く分からなかった確率の問題が
できるようになってしまう人は多いです。

基本法則をしっかりと身に付けていれば、
問題文に書いてある通りに計算することができれば良いだけなので
今まで理解できなかった問題をいても簡単に解くことができるようになります。

数学はノウハウよりも考え方が大切だということですね。


もう少し詳しく説明しましょう。

基本法則の「和の法則」と「積の法則」は教科書にあるので
教科書を参考にしてください。


スポンサーリンク





ここで確率や場合の数の問題で出てくる計算を思い出してみてください。

足し算、掛け算は良く出てきますよね。
これが和の法則、積の法則で説明できます。

たまに出てくるのが、引き算と割り算ですね。
確率や場合の数における引き算と割り算の意味を考えたことがありますか？

これがとても重要です。

計算の意味を日本語で説明できるようにしてください。
そうすればいとも簡単に問題を解くことができるようになってしまいます。

文章題が苦手だという中学生も同じです。
足し算、引き算、掛け算、割り算の意味を日本語で説明できるようにしてみてください。

これさえできれば、場合の数や確率、文章題は、
書いてあることを数式にして計算ミスさえしなければ
機械的に解くことができるようになります！

わからないことがあれば、
コメントしてください。

できる限りお答えします。

最後までお読みいただきありがとうございます。

スポンサーリンク

高校生からの質問ですが、
中学数学でもたまに出てくる『最短距離の問題』です。

問題はコチラ↓



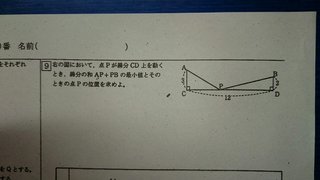
東京大学が昔、光の反射問題を良く出していたみたいです。

最短距離は、普通は直線距離で考えれば良いのですが、
途中で反射する条件が付くと難しくなるようですね。

ただ、最短距離の問題はそのまま暗記してしまっても
良いと思います。なぜなら、あまり応用されることが少ないからです。

しかも、知らないと解けない場合がほとんどです。


スポンサーリンク






今回の問題なら、
点Bの直線CDについて線対称な点を取ります。
それを点B´とします。
２点A,B´を直線で結びます。
直線CDと直線AB´の交点がPです。

ちなみに、PB＝PB´になるのはわかりますよね？


いつもお読みいただき、ありがとうございます。

これからもよろしくお願いいたします！

この記事を読んだ証拠にコチラをクリックしてください↓

数学科・算数教育 ブログランキングへ