となりますから、f'(x) = 0 とおいて

x = ±√2/2
で極値 f(±√2/2) = 1/2 をとることがわかります。f(x) は奇関数ですから、とりあえず 0 < x を描き、あとで原点対称に折り返して負の領域を描くことにします。√2/2 < 3/4 に注意して極値をとる x = √2/2 前後の f'(x) の符号を調べると、

f'(0) > 0,　f'(3/4) < 0
ですから、 f(√2/2) は極大値であることがわかります。
もうひとつ注意しておきたいのが、x = 1 付近における f'(x) の様子です。

x → 1　：　f'(x) → −∞
ですから、この付近で傾きは円と同じように限りなく垂直に近づきます。以上のことを考慮してグラフを描くと下図のようになります。

　

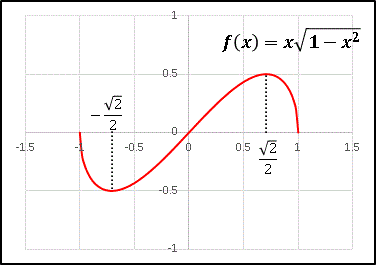
(2) 先程も述べたように、f(x) は奇関数ですから、0 から 1 まで積分した値 S/2 を求めて、最後に 2 倍します。この形の関数を積分するときには、

x = sinθ
と変数変換するのがコツです。

θ：0 → pi/2、　dx = cosθdθ
ですから、積分は

画像
のようになります。この積分を実行するときは、

　　　(cos3θ)' = 3cos2θ(−sinθ)

　　　⇔　(−cos3θ/3)' = cos2θsinθ

の関係を