≫ [Amazon書籍] 理系のためのキャリアデザイン（戦略的就活術）

立ち上がりに特徴がある関数です　今回はあまり見慣れない関数を扱ってみます：

y = xa/x　　　[1]
　式を眺めているだけでは、どうにも概形を想像しにくいですね。
　早速グラフを描いてみます；

　

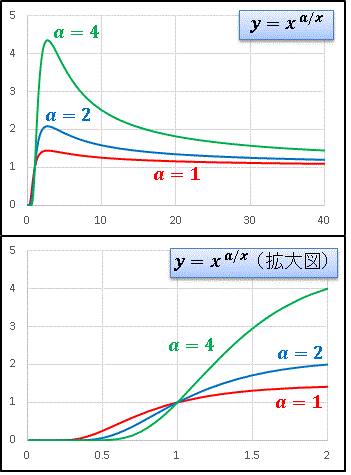
　原点付近で急速に立ち上がって最大値に達したあとに値を落としていきますが、 a の値の増加にともなって、頂点から x 軸正方向への勾配も急激になります。実はこの関数、立ち上がりにも特徴があります。原点付近の拡大図を見ると、 a の値が大きいほど立ち上がりは遅くなっていることがわかります。これは x < 1 ではその指数が大きいほど値が小さくなることに対応しています。
　さて、図を見ると「 a の値によらず 1 に収束するのではないか？」という予想が立ちますね。証明してみましょう。 [1] のままでは扱いにくいので両辺の対数をとってみます：

logy = a(logx/x)
　ここで x → ∞ で logx/x → 0 [*] が知られていますから、

logy → 0　⇔　y → 1　（x → ∞）
となって [1] は 1 に収束します。（証明終わり））

x → ∞ で logx/x → 0 の証明