必ず極小値が存在します 前回記事で「 x → ∞ のとき logx/x → 0 」を証明するときに、
y = √x - log(x)
という関数が登場しました。今回はこれをもう少し一般化して
y = xa - blog(x) (x > 0) [1]
という関数を扱ってみます。 x > 0 ですから a は任意の実数をとることができますが、関心があるのは 0 < a < 0.5 の辺りのふるまいです。まずは b = 1 に固定して a = 0.5, 0.4, 0.3 というように変化させてみます：
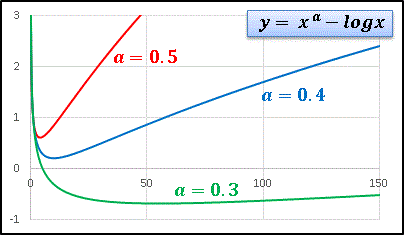
この関数が a の僅かな変化に対して非常に敏感に応答することがわかります。兮 = 0.1 の小さな刻み幅であってもグラフ全体がどんどん下に落とされていきますね。次は a = 0.5 に固定して b の値を変化させます：
コメント(0)
目次