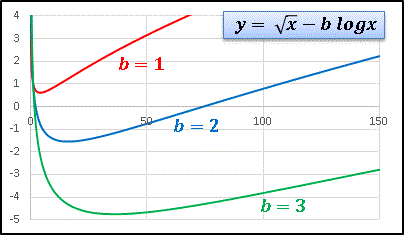
先程のように sensitive ではありませんが、b が増加するとやはりグラフは下へ落ちます。
　さてここで、もう１度前回に証明した公式

画像
を思い出してください。logx に係数 b をかけてもやはり 0 に収束します。

　a がどれほど小さくなろうと、或いは b をどれほど大きくしようと、十分に大きな x においては xa が blogx に優ります。したがって必ずどこかで増加へ転じます。つまりこの関数には必ず極小値が存在します。それでは極値をとる x はどのような方程式を満たすのか調べてみましょう。 [1] を微分すると

y´= axa-1 - b/x
ですから、y´= 0 とおくと

x = (b/a)1/a
が得られます。極小値は a, b についての 2 変数関数として

MIN(a, b) = (b/a)[1-log(b/a)]
と表されます。つまり極小値は a と b の比率 k = b/a の関数になっていますね。
　改めて k の関数として書き直しておきましょう：

MIN(k) = k [1 - logk]　　[2]
　たとえば、a = 0.5, b = 1 であれば k = 2 ですから、

MIN(2) = 2[1-log2] = 0.614
と計算できます。
　
才能について