C++，C++/CX に挑戦！

fmod関数（p.63）で実数の剰余を求めることができます。

（例１）　2.4　÷ 1.5
　　　　fmod(2.4, 1.5) で 2.4 を 1.5 で割ったときの剰余を求めることができます。
　　　　電卓で 2.4　÷ 1.5 を計算すると、割り切れて 商は1.6 です。
　　　　割り切れるのなら 剰余は 0 のはずだから、fmod(2.4, 1.5) は 0 になるような気が
　　　　してしまいますが、そうではありません。

　　　　fmod(2.4, 1.5) は 0.9 になります。なぜだかわかりますか？
　　　　fmod関数は、「商は整数である」 と考えているようです。
　　　　2.4 の中に 1.5 は1つしか含まれないので、
　　　　　　商は 1
　　　　　　剰余は 2.4 − 1.5 × 1 を計算して 0.9
　　　　ということになります。

（例２）　2.4　÷ 2.5
　　　　2.4 の中に 2.5 は含まれないので、
　　　　　　商は 0
　　　　　　剰余は 2.4
　　　　です。

（例３）　3.1　÷ 1.5
　　　　3.1 の中に 1.5 は2つ含まれるので、
　　　　　　商は 2
　　　　　　剰余は 0.1
　　　　です。

#include <cmath>
#include <iostream>
using namespace std;

int main()
{
    double x;

    cout << "実数値："; cin >> x;

    if (double m = fmod(x, 1.5)) {
        cout << "その値は1.5で割り切れません。\n";
        cout << "剰余は" << m << "です。\n";
    }
    else {
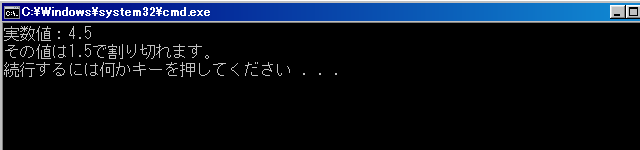
        cout << "その値は1.5で割り切れます。\n";
    }
}

--