ヒロセ通商・口座開設はこちら
自然界と人体の神秘 〜フィボナッチ数列、黄金比から垣間見える〜
子供(中学1年生)の夏休みの数学自由課題を手伝っていたら、とても興味深いことを知りました。今回のブログは「咳痰」「呼吸器」にはほとんど関連ありませんが、数列/数学を通じて自然界や宇宙にまで通する「法則」「真理」を垣間見るような感覚になり、神秘的な気持ちになれたらと思います。
「自然という書物は数学の言葉で書かれている」(ガリレオ・ガリレイ)
自然界に多くみられる数列〜フィボナッチ数列〜
イタリアの数学者フィボナッチ(1170~1259年頃)が紹介した数列を「フィボナッチ数列」と言います。
1、1、2、3、5、8、13、21、34、55、89、144、233、377…
「どの数字も前2つの数字を足した数字」という規則の数列です。何が不思議だと思います?実は自然界にはこの数列が多く潜んでいます。
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13
8+13=21…
数学者のフィボナッチは「ウサギの増える」様子をみて、この数列を見つけたそうです。
子ウサギを観察し、1か月には大人(1つがい)になり、2か月後には子ウサギを産んで2つがいになりました。3か月目には3つがい、4ヶ月目には5つがい、5か月目には8つがい、ウサギは「1、1、2、3、5、8.13、…」と増えることを観察しました。

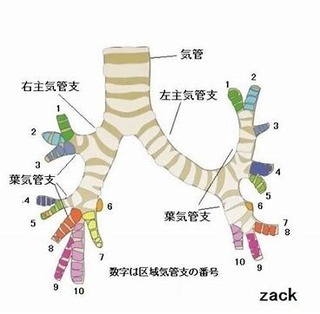
またほとんどの木はフィボナッチ数列によって「枝分かれ」していくそうです。よくよく見ると人体の「気管支の枝分かれ」や「肝臓の血管の枝分かれ」も同様に分岐しています。
また「花びらの枚数」や「松ぼっくりの鱗(うろこ)模様の列数」、「ひまわりの種の列数」はフィボナッチ数が多いことは知ってましたか?自然界の動植物の中に息づく「生命の数」だと思いませんか?
「花びらの枚数」は1、2、3,5、8、13、21,34枚…が多い

「松ぼっくりの鱗(うろこ)模様」
は反時計回りに13回、時計回りに8回、螺旋(らせん)状に並んでいる
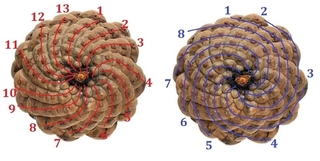
「ひまわりの種」は時計回りに34回、反時計回りに15回並んでいる
フィボナッチ数列から作られる「螺旋形状」 〜木の葉やDNA螺旋…にもみられる〜
「松ぼっくり」や「ひまわりの種」の並び方は「螺旋(らせん)形」です。どうしてこのような形状になるのでしょうか?この形状は強度を保つため、効率的に成長するのに合理的であり、植物が自然界で生存するために必然的に現れたものであり、「生命の曲線」と言われています。

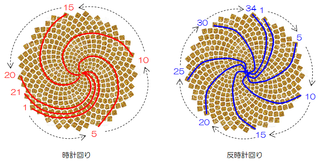
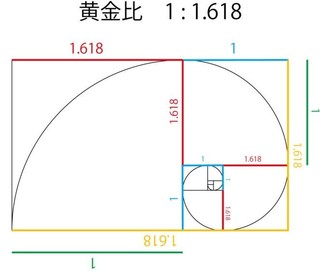
これもフィボナッチ数列に関連しています。下図のように1辺の長さが「1、1、2、3、5、8、13、21、…(フィボナッチ数列)」の四角形を並べると渦巻き状に並べることが出来ます。正方形の辺を半径とした円を描くと「螺旋(らせん)」が広がっていきます。
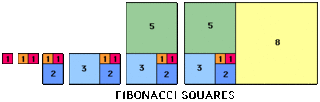
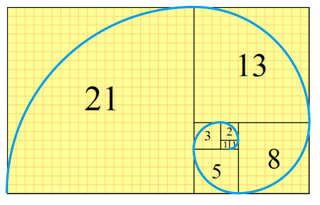
この「螺旋(らせん)」の形状は自然界であらゆるところで観察されます。
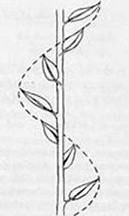
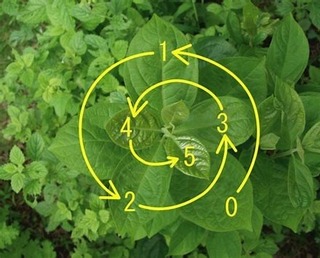
「植物の葉」は茎の成長と共に「螺旋状」に葉を付け、茎を中心にして2方向、3方向、5方向、8方向に生えていきます。この生え方をすることによって、自然と葉同士が重ならずに、光合成の効率を上げるようになっています。

更には「人のDNAの2重螺旋構造」、「台風の渦巻き」、「銀河の渦巻き」にも見られ、自然や宇宙の法則を垣間見た気持ちになりませんか?(サイエンスチャンネル「自然にひそむ数と形」参照)

黄金比 〜ヒトに刻まれた美的感覚、更には為替予測まで〜
「黄金比」とは人間が最も美しいと感じる比率のことで、「ミロのヴィーナス」、「モナ・リザ」、「パルテノン神殿」、「サクラダ・ファミリア」、エジプトの「ピラミッド」など古代より西洋の美術作品や建築物などに取り入れられてきました。




エジプト「ピラミッド」、古代ギリシャの 「パルテノン神殿」の高さ:底辺=1:1.6
黄金比は「1:(1+√5)÷2」=1.618…です。
これはフィボナッチ数列の隣り合う数字の比と一致します。とても不思議ですね。
1/1=1
2/1=2
3/2=1.5
5/3=1.666…
8/5=1.6
13/8=1.625
21/13=1.615384…
34/21=1.619047…
55/34=1.617647…
89/55=1.618181…
144/89=1.617877…
233/144=1.618055…
377/233=1.618025…
610/377=1.618037…
987/610=1.618032…
1597/987=1.618034…
自然界に通じる「黄金比」をヒトは美しいと感じるのでしょうか。黄金比で作られた四角形を「黄金四角形」、螺旋を「黄金螺旋(らせん)」といい、これを取り入れた美術作品や建築物は古今東西を問わず多く観察されます。身近なものでは名刺や各種カード、TV画面の大きさ、各種デザイン(アップル、グーグル等)にも採用されています。



葛飾北斎の嶽三十六景『神奈川沖浪裏』には各種に黄金比率や黄金螺旋が各種に取り入れられている
更には為替の予測にもフィボナッチ数列を用いた比率を利用するようですから、自然界(動植物の螺旋構造や台風/銀河の渦巻き)〜人間界(DNAや構造、美的感覚)〜果ては未来(の予測)にまでフィボナッチ数列は関連しているのですから、まさに「神秘的な数列」とは思いませんか?
低予算でも始められるFX会社
・みんなのFX
・ヒロセ通商
・JFX株式会社
最後に音楽に取り入れたもの(Encoding the Fibonacci Sequence Into Music)はとても美しいメロディな作品で秀逸ですので是非聞いてみてください。きっと「神秘的な気持ち」を味わえることと思います。











