2017年04月05日
計算機プログラムの構造と解釈 問題1.7
計算機プログラムの構造と解釈(SICP)の問題1.7について。
実装は以下の通り。
例えば、
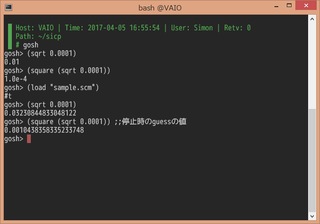
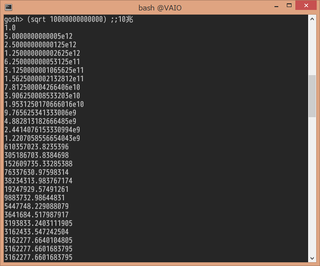
例えば、10兆の平方根を求めようとすると途中からguessの値が変化しなくなり無限ループに陥る。
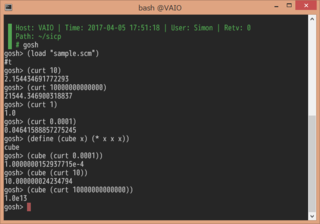
SICPの問題1.7を素直に実装してみました。ある繰り返しから次の繰り返しのguessが許容値未満しか変化しなかったときに停止します。許容値を小さくすれば正確さが高くなります。
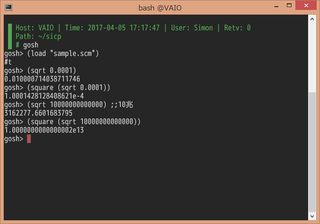
小さい値や大きい値にもある程度正確な結果を返しています。

実装は以下の通り。
;;;Newton法 p.13
(define (sqrt-iter guess x)
(if (good-enough? guess x)
guess
(sqrt-iter (improve guess x)
x)))
(define (improve guess x)
(average guess (/ x guess)))
(define (average x y)
(/ (+ x y) 2))
(define (good-enough? guess x)
(let ((tolerance 0.001))
(< (abs (- (square guess) x)) tolerance)))
(define (sqrt x)
(sqrt-iter 1.0 x))
非常に小さい数のとき
例えば、
(sqrt 0.0001)など、許容値0.001を下回る数値の平方根を求めようとすると、guessの値の小数点以下3桁が許容値以下となると再帰呼び出しが停止する。

非常に大きい数のとき
例えば、10兆の平方根を求めようとすると途中からguessの値が変化しなくなり無限ループに陥る。

guessの変化の値に注目したgood-enough?
SICPの問題1.7を素直に実装してみました。ある繰り返しから次の繰り返しのguessが許容値未満しか変化しなかったときに停止します。許容値を小さくすれば正確さが高くなります。
(define (good-enough? guess next-guess)
(let ((tolerance 0.0001))
(< (abs (- next-guess guess)) tolerance)))
(define (sqrt-iter guess x)
(let ((next-guess (improve guess x)))
(if (good-enough? guess next-guess)
next-guess
(sqrt-iter next-guess x))))

小さい値や大きい値にもある程度正確な結果を返しています。
 | 新品価格 |
【このカテゴリーの最新記事】
-
no image
-
no image
この記事へのコメント
コメントを書く
この記事へのトラックバックURL
https://fanblogs.jp/tb/6131962
※ブログオーナーが承認したトラックバックのみ表示されます。
この記事へのトラックバック