組合せの概念を実数世界に広げます
　n 個のものから k 個とる組合せの数は
　
画像
で表されます。たとえば n = 20 の場合に、k の関数として 20Ck をプロットすると次のように、左右対称のグラフが描かれます。

　

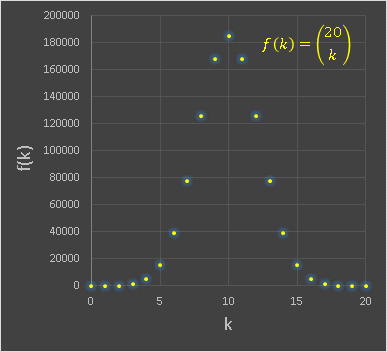
　組合せの式においては n も k も整数なので、nCk も整数値しかとれませんが、ここで階乗を実数範囲まで拡張したガンマ関数
　
画像
を使うと、組合せの数を求める式も実数範囲まで拡張することができます。すなわち、s 個のものから x 個選ぶ数 (s, x はともに実数)を組合せ関数
　
画像
によって定義すれば「 8.5 個のものから、2.3 個をとる組合せの数」という奇妙なものも計算できるわけです（もはや現実世界の事象とは対応していません）。変数が実数に拡張されたのでグラフも滑らかにつながります。さきほどの 20Ck に対応して C(20, x) のグラフを描いてみると次のようになります。