≫ [Amazon 書籍] 情報理論のための数理論理学 (数学のかんどころ)

問題75　都立東池袋高校でアンケート [中１★★☆☆☆]　都立東池袋高校の生徒 300 人に対してアンケートをとったところ、英語が好きな生徒の 8 割が国語も好きだと答えました。また国語が好きな生徒の 6 割が英語も好きだと答えました。70 人の生徒はどちらも好きではないと答えました。英語が好きな生徒は何人いますか？
[ヒント] 前回の問題より少しだけ難しくなっていますが考え方は同じです。「比で考える」という算数的思考法を身につけておくと色々な問題で応用が効きます。
　
問題 75 の解答　どちらも好きではないと答えた 70 人は関係ないので、残り 230 人について考えます。状況を線分で表してみると次のようになります。

　

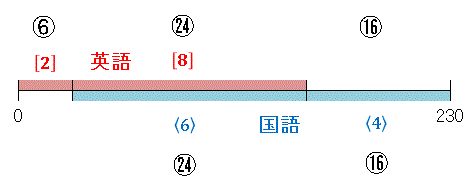
　真ん中（英語と国語の両方が好きな生徒の人数）は重なっているので人数が同じはずです。つまりこの部分を表す比率を「 8 と 6 の最小公倍数 24 」に揃えておきます。[2] や 〈4〉 で表されている部分もそれぞれ 2 倍、4 倍すれば共通の物差しができますね。これをもとに英語が好きな生徒の数を計算すると

230 × 30/46 = 150 人
となります。こういう問題を見ると反射的に「ベン図を描いて方程式だ！」と思ってしまいがちですが、線分を用いたほうが比率の情報を書き込めるので有利なこともあるのです。