リーを g(x), また g(x) から k を引いた関数を f(x) とします：
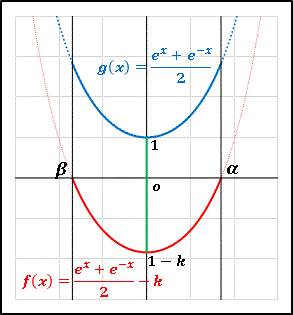
　図をよく見て f(x) と g(x) の位置関係を把握してください。

　

(1) カテナリーが満たす方程式を確認する問題です。
　2y = ex + e−x を 2 乗すると

　　　　　4y2 = e2x + e−2x + 2　　　[1]

　また 2y′= ex − e−x を 2 乗すると

　　　　　4y′2 = e2x − e−x − 2

　両辺に 4 を加えて

　　　　　4y′2 + 4 = e2x − e−2x + 2　　　[2]

　[1] と [2] から

　　　　　1 + y′2 = y2

　が成り立ちます。カテナリーは 2 回微分すると元の形に戻ります。
　2y′= ex − e−x をもう１度微分すると

　　　　　2y′= ex + e−x

となって y" = y が示されました。

(2) まず α, β を求めておきます。
　f(x) = 0 とおいて、 ex = t の変換を行うと、

　　　　　t2 − 2 kt + 1 = 0
　　　　　t = k ± sqrt(k2 − 1)

　変数を元に戻して、

　　　　　ex = k ± sqrt(k2 − 1)

　対数を取れば α, β を得られますが、以下の積分計算を考えて、このままの形にしておきます。つまり、

　　　　　eα = k + sqrt(k2 − 1)
　　　　　eβ = k − sqrt(k2 − 1)

　計算に備えて次の形も用意しておきます：

　　　　　eα − eβ = 2 sqrt(k2 − 1)
　　　　　eα eβ = 1