b = 500　　H = 1000/501 = 1.996

　このあたりで「おや」と思いませんでしたか？
　b = 100 と b = 500 でほとんど値に変化がありません。それ以前に、
　「こんなに大きな値を入れたのに、平均値がこんなに小さいの？」
　「 1 と 500 の平均値が 1.996 なんて、ありえなくない？」
　と思ってしまいますよね。

(3) もう少し解析的に見てみましょう。
　　H(x) は x > 0 で定義されることに注意してください。
　　商の微分公式を用いて H(x) の導関数を求めます：

画像
　ゆえに H(x) は単調増加関数です。
　H(x) の分母・分子を x で割って x ⇒ +∞ の極限をとると H(+∞) = 2a 。
　以上より 2a を漸近線とする簡単なグラフが描けます：

　

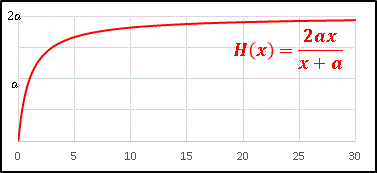
　つまり、調和平均 H は b をどれだけ大きくしても決して 2a を超えられなのです。
　
調和平均の意味　実は調和平均というのは平均時速を得るために用いられます。
　たとえば、往路・帰路ともに 1km の道のりを往復することを考えます。
　往路は徒歩（時速 a = 4 km/h）で、
　帰路は超伝導リニア（時速 b = 500 km/h）に乗ります！
　「たった 1km をリニアで