2 であろうと、メルセンヌ素数 2257 - 1 であろうと）必ず 5 通りです。何だか不思議ですね。

(2) 上で求めた (m, n) に 2 を入れて計算するだけです。答えは、

　　　　　(m, n) = (3, 6), (4, 4), (6, 3), (1, - 2), (- 2, 1)

　の 5 通りです。

解説　 1/m + 1/n = 1/p を満たす (m, n) の組がずいぶん少ないなという印象がありますね。そのあたりをグラフで確認してみましょう。そこでまず (m, n) を実数 (x, y) に置き換えて、y = f(x) の形に直してみると、

y = px / [x - p]
という関数が得られます。 p = 2 の場合にグラフを描いてみると ......

　

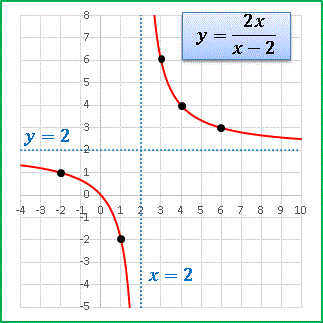
　黒丸が問題の解答となる格子点です。
　見ての通り、漸近線に向かって収束する分数関数ですから、(x, y) ともに整数値をとれる範囲は限られています。その範囲内でちょうど y = f(x) が整数格子点を通るところを見つけようという問題だったのです。そしてその格子点の数は p が素数である限りは、必ず 5 通りであるということです。
　もう１つ注目したいのは上のグラフでは (x, y) = (0, 0) を満たすということ。
　(m, n) = (0, 0) が定義でなかったのは、

1/m + 1/n = 1/p　　　[1]
という式で m と n が分母にあるからです。これがもし、

m = np / [n − p]　　　[2]
を満たす (m, n) を見つけなさいという問題であれば、(0, 0) も含めて構わないということになります。[1] と [2] は式変形によって相互変換可能ですが、[2] ⇒ [1] への変換過程では両辺の逆数