極値の有無の境目を判定します　今回は一見したところとても易しそうな

y = exp(x) − ax 2　　　[1]
という関数を扱います。 a の値をいくつか選んでグラフを描いてみます。

　

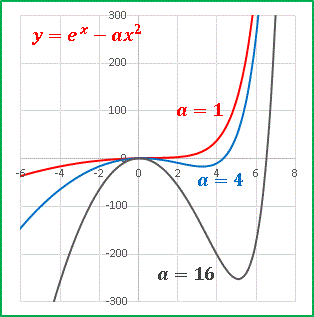
　a の値を大きくするほど深い谷を形成して exp(x) の増加を遅らせます。実はこの関数は a の変遷過程である所を境に「極値をもたない関数」から「極値をもつ関数」へと変化します。その様子を調べるために、[1] を微分して導関数を得ます：

y′ = exp(x) − 2ax　　　[2]
　この導関数のグラフも描いてみます。

　

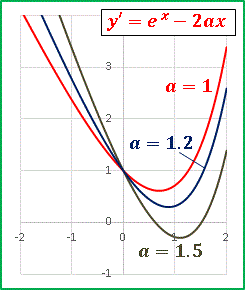
　y′ のグラフが x 軸と交点を持てば [2] は極値をもちます。
　a = 1.2 ではまだ極値はありませんが、a = 1.5 は極値ありです。
　そこで a の値を変化させて「どこで x 軸と接するか」ということを調べます。これは VBA でプログラムを書いて計算させるわけですが、簡単にその構造を説明すると「 a の値を 0.001 刻みに変化させて、y′ の値が１つでも負の値をとった瞬間に計算を止めて、そのときの a を閾値とみなす」というものです。正確に言えば、「計算を止めた a 」と、「その直前の a 」との間に閾値があります。刻み幅を小さくすればより精度の高い値を得る