ことができます。実際にそのプログラムを実行すると、次のような結果を得ます。

　a = 1.360 で計算終了
　　x = 0.96　y = 0.000496
　　x = 0.97　y = - 0.000456

　

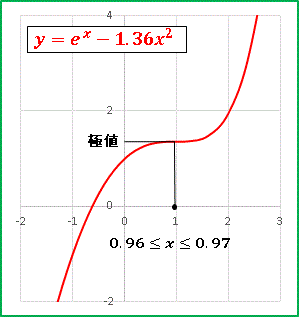
　a = 1.360 が閾値です。この値を近似的にグラフが x 軸に接する a であると考えると、このとき y′= 0 の解 x = xm はひとつだけであり、 x = xm の前後で y′の符号は変化しません。したがって極値はもちません。ただ厳密に考えると a = 1.360 で僅かに x 軸と交差しているので y′ = 0 の解は２つあり、その解 α と β （α < β）は非常に近い値をとります。そしてその前後で y′ もまた微妙に変化して、x = α のところで上に凸（極大値）、x = β のところで下に凸（極小値）が現れます。ごく狭い範囲に極大値と極小値が出現しているのです。文章でずらずら書いても何が何だかわからなくなりそうなので、a = 1.370 としたグラフで極値付近を範囲を拡大してみます：

　

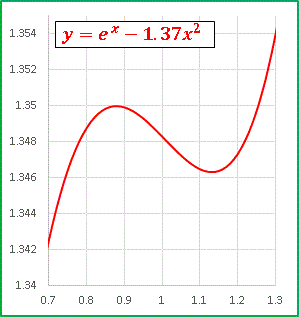
　ちゃんと凹凸が現れています。

x = α = 0.88 のとき極大値 1.350
x = β = 1.14 のとき極小値 1.346
となります。極大・極小といっても普通のグラフでは