今回のテーマは高校数学でよく扱われる２次関数の頂点の軌跡です。

２次関数の頂点の軌跡
　パラメータ a を含んだ２次関数

y = x 2 + ax　　　[1]
を解析してみます。

　

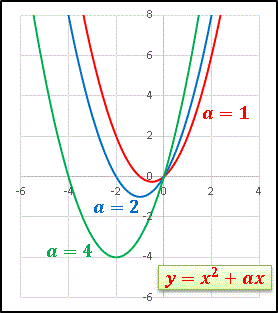
　a が変化するとそれに連動して頂点が動きます。
　その軌跡の方程式を求めてみましょう。[1] を変形して

y = (x + a / 2) 2 − a 2 / 4
ですから、頂点の座標は

(X, Y) = (− a / 2, − a 2 / 4)　　　[2]
となりますね。 a を消去すれば

Y = − X 2　　　[3]
という軌跡の方程式が得られます。これを図示してみると ......

　

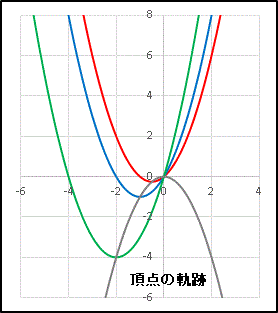
　Y = − X 2 に沿って頂点が移動しているのが分かります。


3 次元グラフで頂点の動きを確認してみます　実は３次元グラフを使うと頂点がどのように動くかひと目でわかります。
　a もまた変数と考えて、

f(x, a) = x 2 + ax　　　[4]
という２変数関数のグラフを描いてみると ......