漸近線で分割される関数　高校数学では次のような関数のグラフを描く問題をよく目にします：

画像
　分母を因数分解すると

画像
となりますから、この関数は x = ±1 で定義できません。

実際にグラフを描いてみると ......

　

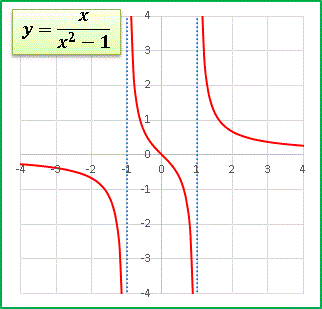
　x = ±1 は漸近線です：

　　x → 1 + 0 （1 に x 軸右側から近づく）とき + ∞
　　x → 1 - 0 （1 に x 軸左側から近づく）とき - ∞

　　x → - 1 + 0 （ - 1 に x 軸右側から近づく）とき + ∞
　　x → - 1 - 0 （ - 1 に x 軸左側から近づく）とき - ∞

　このように、分母が x の多項式で分母 = 0 とおいたときに２つの解を持てば、y = f(x) はグラフは２つの y 軸に平行な漸近線によって３つの領域に分割されます。もう１つ例を見てみましょう：

画像
　先程と同じように分母を因数分解すると

画像
となるので、この関数は x = - 2 と x = 3 という２つの漸近線によ