って領域が分けられます。

　

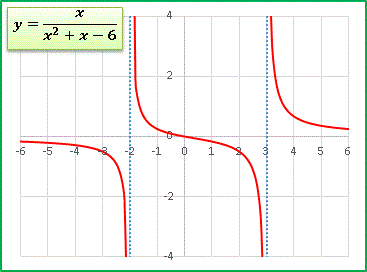
　このタイプの関数は、分母 = 0 の解が得られるなら、増減表を書かなくてもグラフの概形を描くことができます。 y 軸に平行な漸近線を挟んで ±∞ のどちらに発散するかは次のように判定します。たとえば上の例で x = 3 の右側を調べたいのなら、x = 3 + εとおいて（ε はとても小さな正数です）、

　　分母 = (3 + ε) 2 + x + ε - 6 = ε 2 + 7ε + 2 > 0

となるので + ∞ に発散することがわかります。実際には分母をひと目みて暗算でぱっと出てくるぐらいに訓練しておきましょう。もちろん試験の答案では増減表を書かなくてはいけませんが、上の方法で先にグラフを描いてしまっておけばミスが少なくなります。

　補足しておくと、今回の例では１次関数を２次関数で割っているわけですから、 x = ±∞ においては y ≒ 1 / x のように振る舞います。したがって両端では y → ± 0 に収束します。符号については、そのグラフの存在領域の境界となる漸近線における発散の符号と一致します。上のグラフで説明すると、 x → 3 + 0 で y → + ∞ でしたから、x → + ∞ で y → + 0 となります。最後におまけです。三角関数を掛けたり加えたりすると、各領域ごとに振動する関数になります：