く扱う予定です。

　さて、ここでまとめの意味をかねて「実数の数直線」を見てみましょう。「実数」は複素数のすぐ下に分類される数でしたね。

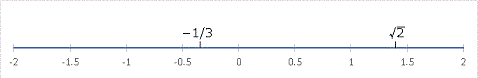
　実数というのは「上の全ての数直線を満たす数」です。もし満たさなければ、数直線は線ではなくなって、途切れ途切れになってしまいます。みっともないですよね。そんなのはとても線とはよべません。ただの切れ端です。言い換えると、整数と分数、無理数をすべて使えば数直線は完全に埋め尽くされるのです。これを少し難しい言葉で言うと、「実数は連続である」といいます。この「連続である」という概念は初等段階ではあまり気にしなくてもよいのですが、数学の勉強を進めていくと大切な概念として再登場します。頭の隅に置いておいてくださいね。
　今のところ実数の連続性に関わってくるのは、閉区間と開区間という考え方です。中学校の早い段階で不等号の使い方は勉強しますね。

−1 ≦ x ≦ 1
という記号です。「−1 以上で 1 以下の数」です。これを閉区間といいます。別の記号を使って [a,b] と書くこともできます。なぜ閉じているというのでしょうか？　それは次の開区間を見ることでわかってきます。

−1 < x < 1
これを開区間、別の記号で {−1,1} と書くのですが、とても深い意味をもっています。x は端の −1 や 1 の値をとれませんが、そこに限りなく近づくことはできます。ちょっと試してみましょう。 1 に近い数として 0.99 あたりをとってみましょう。近いですね。あと少しで端にぶつかってしまいそうな