C++，C++/CX に挑戦！

2017年12月31日

《その214》クロスキャスト（２）　&　p.259演習7-3

　クロスキャスト

　クラス C は、多重継承により、クラス A から純粋仮想関数 fa を、クラス B から純粋仮想関数 fb を受け継いでいます。下のプログラムです。

　クラス C のオブジェクトは、２つの整数値 x, y をデータメンバに持ち、
　　　関数 fa は和ｘ+ｙを、
　　　関数 fb は差 x - y を、
それぞれ返却します。

　main関数では、C型オブジェクトを３つ生成して、それらを、
A*型のポインタ a[0], a[1], a[2] が指しています。
その結果、例えば、

　　　A[0]->fa();

とすれば、メンバ関数 fa を呼び出すことができます。しかし、

　　　A[0]->fb();

でメンバ関数 fb を呼び出すことはできません。
関数 fb は、クラス A からではなく、クラス B から受け継いだものだからです。

　そこで、ポインタ A[0] を A*型から B*型にキャストすることにします。
クラス A とクラス B は、まったく別のクラスで、親子関係もありませんから、本来であればキャストは不可能です。
ところが、クラス A, B には、共通の子クラス C が存在します。
このようなときには、dynamic_cast<>演算子を用いてキャストを成功させることができます。
この形式のキャストは、クロスキャストと呼ばれます。

　他人だったときにはキャストできなかった男女 A, B に、共通の子供 C ができると、A, B は、もう他人ではないのでキャストが可能になる、といった感じでしょうか (∩。∩;)ゞ

　　　B* p = dynamic_cast<B*>(a[0]);
　　　p->fb();

で、メンバ関数 fb を呼び出すことが可能になります。


// ------------------------------------
#include <iostream>
using namespace std;

class A {
public:
    virtual int fa() = 0;
};

class B {
public:
    virtual int fb() = 0;
};

class C : public A, public B {
    int x;
    int y;
public:
    C(int s, int t) : x(s), y(t) { }
    int fa() { return x + y; }
    int fb() { return x - y; }
};

int main()
{
    A* a[] = {
        new C(20, 10),
        new C(50, 30),
        new C(66, 33),
    };

    for (int i = 0; i < 3; i++)
        cout << a[i]->fa() << " ";
    cout << '\n';

    for (int i = 0; i < 3; i++) {
        B* p = dynamic_cast<B*>(a[i]);
        cout << p->fb() << " ";
    }
    cout << '\n';

    for (int i = 0; i < 3; i++)
        delete a[i];
}
// ------------------------------------

新版明解C++中級編　p.259 演習7-3
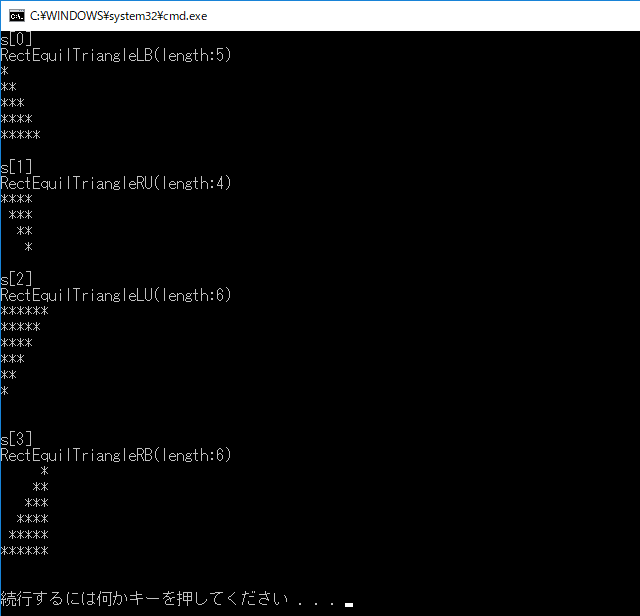
　次のプログラムに、左上直角の二等辺三角形 RectEquilTriangleLU と右下直角の二等辺三角形 RectEquilTriangleRB を作成して加えよ。


// ------------------------------------
#include <string>
#include <sstream>
#include <iostream>

// 図形クラス（抽象クラス）
class Shape {
public:
    virtual ~Shape() = 0;
    virtual Shape* clone() const = 0;
    virtual void draw() const = 0;
    virtual std::string to_string() const = 0;

    void print() const {
        std::cout << to_string() << '\n';
        draw();
    }

    virtual void debug() const = 0;
};
inline Shape::~Shape() { }

inline void Shape::debug() const {
    std::cout << "-- デバッグ情報 --\n";
    std::cout << "型：" << typeid(*this).name()
        << '\n';
    std::cout << "アドレス：" << this << '\n';
}


// 挿入子の多重定義
inline std::ostream& operator<<(
    std::ostream& os,
    const Shape& s
    ) {
    return os << s.to_string();
}


// ２次元クラス（抽象クラス）
class TwoDimensional {
public:
    virtual ~TwoDimensional() = 0;
    virtual double get_area() const = 0;
};
inline TwoDimensional::~TwoDimensional() {}


// 直角二等辺三角形クラス（抽象クラス）
class RectEquilTriangle
    : public Shape, public TwoDimensional {
protected:
    int length;
public:
    RectEquilTriangle(int len) : length(len) { }

    double get_area() const {
        return length * length / 2.0;
    }
};


// 左下直角二等辺三角形クラス
class RectEquilTriangleLB
    : public RectEquilTriangle {
public:
    RectEquilTriangleLB(int len)
        : RectEquilTriangle(len) { }

    RectEquilTriangleLB* clone() const {
        return new RectEquilTriangleLB(length);
    }

    void draw() const {
        for (int i = 1; i <= length; i++) {
            for (int j = 1; j <= i; j++)
                std::cout << '*';
            std::cout << '\n';
        }
    }

    std::string to_string() const {
        std::ostringstream os;
        os << "RectEquilTriangleLB(length:"
            << length << ")";
        return os.str();
    }

    void debug() const {
        Shape::debug();
        std::cout << "クラス：RectEquilTriangleLB\n";
        std::cout << "アドレス" << this << '\n';
        std::cout << "length：" << length << '\n';
    }
};


// 右上直角二等辺三角形クラス
class RectEquilTriangleRU
    : public RectEquilTriangle {
public:
    RectEquilTriangleRU(int len)
        : RectEquilTriangle(len) { }

    RectEquilTriangleRU* clone() const {
        return new RectEquilTriangleRU(length);
    }

    void draw() const {
        for (int i = 1; i <= length; i++) {
            for (int j = 1; j <= i - 1; j++)
                std::cout << ' ';
            for (int j = 1; j <= length - i + 1; j++)
                std::cout << '*';
            std::cout << '\n';
        }
    }

    std::string to_string() const {
        std::ostringstream os;
        os << "RectEquilTriangleRU(length:"
            << length << ")";
        return os.str();
    }

    void debug() const {
        Shape::debug();
        std::cout << "クラス：RectEquilTriangleRU\n";
        std::cout << "アドレス" << this << '\n';
        std::cout << "length：" << length << '\n';
    }
};


int main()
{
    Shape* s[] = {
        new RectEquilTriangleLB(5),  // 左下直角
        new RectEquilTriangleRU(4),  // 右上直角
    };

    for (int i = 0; i < sizeof(s) / sizeof(s[0]); i++) {
        std::cout << "s[" << i << "]\n";
        s[i]->print();
        std::cout << '\n';
    }

    for (int i = 0; i < sizeof(s) / sizeof(s[0]); i++)
        delete s[i];
}
// ------------------------------------

　以下が、解答のプログラムです。

 
#include <string>
#include <sstream>
#include <iostream>

// 図形クラス（抽象クラス）
class Shape {
public:
    virtual ~Shape() = 0;
    virtual Shape* clone() const = 0;
    virtual void draw() const = 0;
    virtual std::string to_string() const = 0;

    void print() const {
        std::cout << to_string() << '\n';
        draw();
    }

    virtual void debug() const = 0;
};
inline Shape::~Shape() { }

inline void Shape::debug() const {
    std::cout << "-- デバッグ情報 --\n";
    std::cout << "型：" << typeid(*this).name()
        << '\n';
    std::cout << "アドレス：" << this << '\n';
}


// 挿入子の多重定義
inline std::ostream& operator<<(
    std::ostream& os,
    const Shape& s
    ) {
    return os << s.to_string();
}



// ２次元クラス（抽象クラス）
class TwoDimensional {
public:
    virtual ~TwoDimensional() = 0;
    virtual double get_area() const = 0;
};
inline TwoDimensional::~TwoDimensional() {}



// 直角二等辺三角形クラス（抽象クラス）
class RectEquilTriangle
    : public Shape, public TwoDimensional {
protected:
    int length;
public:
    RectEquilTriangle(int len) : length(len) { }

    double get_area() const {
        return length * length / 2.0;
    }
};



// 左下直角二等辺三角形クラス
class RectEquilTriangleLB
    : public RectEquilTriangle {
public:
    RectEquilTriangleLB(int len)
        : RectEquilTriangle(len) { }

    RectEquilTriangleLB* clone() const {
        return new RectEquilTriangleLB(length);
    }

    void draw() const {
        for (int i = 1; i <= length; i++) {
            for (int j = 1; j <= i; j++)
                std::cout << '*';
            std::cout << '\n';
        }
    }

    std::string to_string() const {
        std::ostringstream os;
        os << "RectEquilTriangleLB(length:"
            << length << ")";
        return os.str();
    }

    void debug() const {
        Shape::debug();
        std::cout << "クラス：RectEquilTriangleLB\n";
        std::cout << "アドレス" << this << '\n';
        std::cout << "length：" << length << '\n';
    }
};



// 右上直角二等辺三角形クラス
class RectEquilTriangleRU
    : public RectEquilTriangle {
public:
    RectEquilTriangleRU(int len)
        : RectEquilTriangle(len) { }

    RectEquilTriangleRU* clone() const {
        return new RectEquilTriangleRU(length);
    }

    void draw() const {
        for (int i = 1; i <= length; i++) {
            for (int j = 1; j <= i - 1; j++)
                std::cout << ' ';
            for (int j = 1; j <= length - i + 1; j++)
                std::cout << '*';
            std::cout << '\n';
        }
    }

    std::string to_string() const {
        std::ostringstream os;
        os << "RectEquilTriangleRU(length:"
            << length << ")";
        return os.str();
    }

    void debug() const {
        Shape::debug();
        std::cout << "クラス：RectEquilTriangleRU\n";
        std::cout << "アドレス" << this << '\n';
        std::cout << "length：" << length << '\n';
    }
};



// 左上直角二等辺三角形クラス
class RectEquilTriangleLU
    : public RectEquilTriangle {
public:
    RectEquilTriangleLU(int len)
        : RectEquilTriangle(len) { }

    RectEquilTriangleLU* clone() const {
        return new RectEquilTriangleLU(length);
    }

    void draw() const {
        for (int i = length; i >= 1; i--) {
            for (int j = 1; j <= i; j++)
                std::cout << '*';
            std::cout << '\n';
        }
        std::cout << '\n';
    }

    std::string to_string() const {
        std::ostringstream os;
        os << "RectEquilTriangleLU(length:"
            << length << ")";
        return os.str();
    }

    void debug() const {
        Shape::debug();
        std::cout << "クラス：RectEquilTriangleLU\n";
        std::cout << "アドレス" << this << '\n';
        std::cout << "length：" << length << '\n';
    }
};



// 右下直角二等辺三角形クラス
class RectEquilTriangleRB
    : public RectEquilTriangle {
public:
    RectEquilTriangleRB(int len)
        : RectEquilTriangle(len) { }

    RectEquilTriangleRB* clone() const {
        return new RectEquilTriangleRB(length);
    }

    void draw() const {
        for (int i = 1; i <= length; i++) {
            for (int j = 1; j <= length - i; j++)
                std::cout << ' ';
            for (int j = 1; j <= i; j++)
                std::cout << '*';
            std::cout << '\n';
        }
        std::cout << '\n';
    }

    std::string to_string() const {
        std::ostringstream os;
        os << "RectEquilTriangleRB(length:"
            << length << ")";
        return os.str();
    }

    void debug() const {
        Shape::debug();
        std::cout << "クラス：RectEquilTriangleRB\n";
        std::cout << "アドレス" << this << '\n';
        std::cout << "length：" << length << '\n';
    }
};



int main()
{
    Shape* s[] = {
        new RectEquilTriangleLB(5),  // 左下直角
        new RectEquilTriangleRU(4),  // 右上直角
        new RectEquilTriangleLU(6),  // 左上直角
        new RectEquilTriangleRB(6),  // 右下直角
    };

    for (int i = 0; i < sizeof(s) / sizeof(s[0]); i++) {
        std::cout << "s[" << i << "]\n";
        s[i]->print();
        std::cout << '\n';
    }

    for (int i = 0; i < sizeof(s) / sizeof(s[0]); i++)
        delete s[i];
}

新版明解C 入門編 (明解シリーズ)

新品価格
￥2,916から
(2017/11/10 13:13時点)

新版明解C 中級編 (明解シリーズ)

新品価格
￥2,916から
(2017/11/10 13:14時点)

posted by こうすけ at 19:29 | Comment(0) | TrackBack(0) | （カテゴリなし）

<< 2017年12月 >>
日	月	火	水	木	金	土
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30
31

C++，C++/CX に挑戦！

広告

2017年12月31日

《その214》 クロスキャスト（２） & p.259演習7-3

《その214》クロスキャスト（２）　&　p.259演習7-3