2018年08月05日
《その432》面法線ベクトル,頂点法線ベクトル
面法線ベクトル,頂点法線ベクトル
面に垂直な直線を法線と呼びます。法線方向のベクトルを法線ベクトルといいますが、面から遠ざかる向きが正の向きです。
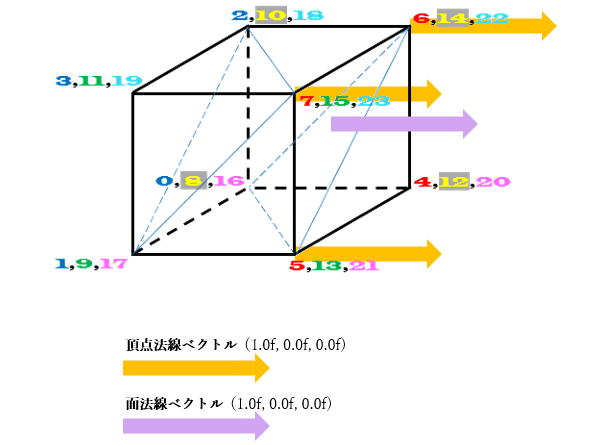
下図において、メッシュを構成する三角形の中の、例えば三角形576の法線ベクトル(面法線ベクトル)は薄紫色で表される右向き(x軸の正の向き)の矢印です。
したがって、 三角形576の面法線ベクトルは(1.0f, 0.0f, 0.0f)です。
※通常、法線ベクトルは、大きさ(長さ)が 1 になるように決めます。
頂点法線ベクトルというのは、頂点を始点とするベクトルです。三角形576のように独立した平面の場合、3つの頂点法線ベクトルは全て面に垂直になります。
よって、各頂点における頂点法線ベクトルは下図の薄オレンジ色で表される右向き矢印です。
この場合の頂点法線ベクトルは、面法線ベクトルと同じで、(1.0f, 0.0f, 0.0f)ということになります。
面法線ベクトルは、光線の向きを表すベクトルとのなす角度を計算することによって面の明るさを決定する ために利用されます。
前回《431》の Sample3DSceneRenderer.cpp 内にある下記のコードが、各頂点の座標と頂点法線ベクトルです。
三角形576のように独立した平面の場合には、面法線ベクトルは 頂点法線ベクトルと同じになります。
static VertexPositionColor verticesPosNrm[24];
// 頂点の座標
verticesPosNrm[ 0].pos = XMFLOAT3(-0.5f, -0.5f, -0.5f);
verticesPosNrm[ 1].pos = XMFLOAT3(-0.5f, -0.5f, 0.5f);
verticesPosNrm[ 2].pos = XMFLOAT3(-0.5f, 0.5f, -0.5f);
verticesPosNrm[ 3].pos = XMFLOAT3(-0.5f, 0.5f, 0.5f);
verticesPosNrm[ 4].pos = XMFLOAT3( 0.5f, -0.5f, -0.5f);
verticesPosNrm[ 5].pos = XMFLOAT3( 0.5f, -0.5f, 0.5f);
verticesPosNrm[ 6].pos = XMFLOAT3( 0.5f, 0.5f, -0.5f);
verticesPosNrm[ 7].pos = XMFLOAT3( 0.5f, 0.5f, 0.5f);
verticesPosNrm[ 8].pos = XMFLOAT3(-0.5f, -0.5f, -0.5f);
verticesPosNrm[ 9].pos = XMFLOAT3(-0.5f, -0.5f, 0.5f);
verticesPosNrm[10].pos = XMFLOAT3(-0.5f, 0.5f, -0.5f);
verticesPosNrm[11].pos = XMFLOAT3(-0.5f, 0.5f, 0.5f);
verticesPosNrm[12].pos = XMFLOAT3( 0.5f, -0.5f, -0.5f);
verticesPosNrm[13].pos = XMFLOAT3( 0.5f, -0.5f, 0.5f);
verticesPosNrm[14].pos = XMFLOAT3( 0.5f, 0.5f, -0.5f);
verticesPosNrm[15].pos = XMFLOAT3( 0.5f, 0.5f, 0.5f);
verticesPosNrm[16].pos = XMFLOAT3(-0.5f, -0.5f, -0.5f);
verticesPosNrm[17].pos = XMFLOAT3(-0.5f, -0.5f, 0.5f);
verticesPosNrm[18].pos = XMFLOAT3(-0.5f, 0.5f, -0.5f);
verticesPosNrm[19].pos = XMFLOAT3(-0.5f, 0.5f, 0.5f);
verticesPosNrm[20].pos = XMFLOAT3( 0.5f, -0.5f, -0.5f);
verticesPosNrm[21].pos = XMFLOAT3( 0.5f, -0.5f, 0.5f);
verticesPosNrm[22].pos = XMFLOAT3( 0.5f, 0.5f, -0.5f);
verticesPosNrm[23].pos = XMFLOAT3( 0.5f, 0.5f, 0.5f);
// 頂点法線ベクトル
verticesPosNrm[ 0].nrm = XMFLOAT3(-1.0f, 0.0f, 0.0f);
verticesPosNrm[ 1].nrm = XMFLOAT3(-1.0f, 0.0f, 0.0f);
verticesPosNrm[ 2].nrm = XMFLOAT3(-1.0f, 0.0f, 0.0f);
verticesPosNrm[ 3].nrm = XMFLOAT3(-1.0f, 0.0f, 0.0f);
verticesPosNrm[ 4].nrm = XMFLOAT3( 1.0f, 0.0f, 0.0f);
verticesPosNrm[ 5].nrm = XMFLOAT3( 1.0f, 0.0f, 0.0f);
verticesPosNrm[ 6].nrm = XMFLOAT3( 1.0f, 0.0f, 0.0f);
verticesPosNrm[ 7].nrm = XMFLOAT3( 1.0f, 0.0f, 0.0f);
verticesPosNrm[ 8].nrm = XMFLOAT3( 0.0f, 0.0f, -1.0f);
verticesPosNrm[ 9].nrm = XMFLOAT3( 0.0f, 0.0f, 1.0f);
verticesPosNrm[10].nrm = XMFLOAT3( 0.0f, 0.0f, -1.0f);
verticesPosNrm[11].nrm = XMFLOAT3( 0.0f, 0.0f, 1.0f);
verticesPosNrm[12].nrm = XMFLOAT3( 0.0f, 0.0f, -1.0f);
verticesPosNrm[13].nrm = XMFLOAT3( 0.0f, 0.0f, 1.0f);
verticesPosNrm[14].nrm = XMFLOAT3( 0.0f, 0.0f, -1.0f);
verticesPosNrm[15].nrm = XMFLOAT3( 0.0f, 0.0f, 1.0f);
verticesPosNrm[16].nrm = XMFLOAT3( 0.0f, -1.0f, 0.0f);
verticesPosNrm[17].nrm = XMFLOAT3( 0.0f, -1.0f, 0.0f);
verticesPosNrm[18].nrm = XMFLOAT3( 0.0f, 1.0f, 0.0f);
verticesPosNrm[19].nrm = XMFLOAT3( 0.0f, 1.0f, 0.0f);
verticesPosNrm[20].nrm = XMFLOAT3( 0.0f, -1.0f, 0.0f);
verticesPosNrm[21].nrm = XMFLOAT3( 0.0f, -1.0f, 0.0f);
verticesPosNrm[22].nrm = XMFLOAT3( 0.0f, 1.0f, 0.0f);
verticesPosNrm[23].nrm = XMFLOAT3( 0.0f, 1.0f, 0.0f);
この記事へのコメント
コメントを書く
この記事へのトラックバックURL
https://fanblogs.jp/tb/7966660
※ブログオーナーが承認したトラックバックのみ表示されます。
この記事へのトラックバック

