《その140》素数かどうかを調べる　&　p.97演習3-2: C++，C++/CX に挑戦！

2017年11月19日

《その140》素数かどうかを調べる　&　p.97演習3-2

　素数であるかどうかを調べる

　ある数が素数であるかどうかを調べる方法は、おそらくいろいろあると思いますが、
ここでは、次のような単純な方法を使います。

　最初は、具体的な数値を使って考えてみます。

◆　17 が素数であるかどうか調べてみます。

　17 を割る数を 2 から 1 ずつ大きくしながら、余りと商（int型の割り算なので商は整数）をチェックしてみます。


　　　　17 % 2 = 1,   17 / 2 = 8
　　　　17 % 3 = 2,   17 / 3 = 5
　　　　17 % 4 = 1,   17 / 4 = 4
　　　　17 % 5 = 2,   17 / 5 = 3

　17 / 5 まで計算しましたが、余りが 0 になることはありませんでした。
このとき、商は 3 で、割る数 5 より小さくなってしまいました。
17 が約数を持っているのなら、ここまでの間に見つかっている（余りが 0 になるときがある）はずです。
よって、17 は素数です。

◆　同じことを 49 でやってみます。

　49 / 6 まで計算しましたが、余りが 0 になることはありませんでした。
このとき、商は 8 で、割る数 6 よりまだ大きいので、割る数をさらに 1 だけ大きくして
49 % 7 を計算してみると、余りが 0 で割り切れました。
よって、 49 は素数ではありません。


　　　　49 % 2 = 1,   49 / 2 = 24
　　　　49 & 3 = 1,   49 / 3 = 16
　　　　49 % 4 = 1,   49 / 4 = 12
　　　　49 % 5 = 4,   49 / 5 =  9
　　　　49 % 6 = 1,   49 / 6 =  8
　　　　49 % 7 = 0,   49 / 7 =  7

このような考え方で、素数を求める関数 prime_num を次のようにしました。
------------------------------------------------

bool prime_num(int x) {
    bool b = true;              // 仮に素数であるとしておく。
    for (int i = 2; i <= x / i; i++) {
        if (!(x % i)) {
            b = false; break;   // 割り切れたら素数ではない。
        }
    }
    return b;
}

------------------------------------------------

　上の関数では、整数 x が素数であるかどうかを調べます。
　x を 2 で割り、3 で割り･･･、と割る数 i を 1 ずつ大きくしていきます。
大きくするといっても、i が x / i より大きくなったらそこで終わりです。x が約数を持っているのなら、ここまでの間に見つかっている（余りが 0 になるときがある）はずです。

新版明解C++中級編　p.97 演習3-2
　指定された条件を満たす要素を配列から線形探索する関数 search_if を作成せよ。
　　　　int search_if(const int a[], int n, bool cond(int));
　第１引数は探索対象の配列であり、第２引数 n は要素数である。第３引数 cond には、条件を満たすかどうかの判定を行うための関数へのポインタを受け取る。条件を満たす要素のうち、最も先頭側の要素の添字を返却すること。ただし、探索に失敗した場合には－1 を返却するものとする。
※ この関数は､たとえば『15 以上 30 以下の要素の探索』､『5 で割り切れる要素の探索』といった､
　任意の条件での探索を可能とする。


// p97_演習3-2
#include <ctime>
#include <cstdlib>
#include <iostream>
using namespace std;

bool mlt_of_17(int x) {
    return x % 17 == 0;
}

bool mlt_of_23(int x) {
    return x % 23 == 0;
}

bool _80_to_90(int x) {
    return x >= 80 && x <= 90;
}

bool prime_num(int x) {
    bool b = true;
    for (int i = 2; i <= x / i; i++) {
        if (!(x % i)) {
            b = false; break;
        }
    }
    return b;
}

int search_if(const int a[], int n, bool cond(int)) {
    int f = -1;
    for (int i = 0; i < n; i++) {
        if (cond(a[i])) {
            f = i;
            break;
        }
    }
    return f;
}

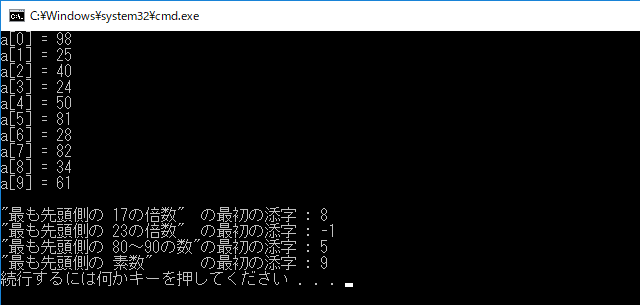
int main() {
    srand((unsigned int)time(NULL));

    int a[10];
    int n1 = sizeof(a) / sizeof(a[0]);
    for (int i = 0; i < n1; i++) a[i] = rand() % 90 + 10;

    for (int i = 0; i < n1; i++)
        cout << "a[" << i << "] = " << a[i] << '\n';
    cout << '\n';
    cout << "\"最も先頭側の 17の倍数\"  の最初の添字 : " << search_if(a, n1, mlt_of_17);
    cout << '\n';
    cout << "\"最も先頭側の 23の倍数\"  の最初の添字 : " << search_if(a, n1, mlt_of_23);
    cout << '\n';
    cout << "\"最も先頭側の 80～90の数\"の最初の添字 : " << search_if(a, n1, _80_to_90);
    cout << '\n';
    cout << "\"最も先頭側の 素数\"      の最初の添字 : " << search_if(a, n1, prime_num);
    cout << '\n';
}