2017年11月16日
《その132》 集合について & p.84演習2-7
集合について
図のような集合があるとします。
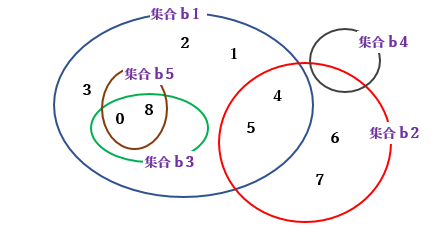
b1 = { 0, 1, 2, 3, 4, 5, 8 }
b2 = { 4, 5, 6, 7 }
b3 = { 0, 8 }
b4 = { }
b5 = { 0, 8 }
b4 は 空集合です b4 = φ
b1 と b2 の和集合 b1 ∪ b2 = { 0, 1, 2, 3, 4, 5, 6, 7, 8 }
b1 と b2 の積集合 b1 ∩ b2 = { 4, 5 }
b1 と b2 の差集合 b1 - b2 = { 0, 1, 2, 3, 8 }
b2 - b1 = { 6, 7 }
b3 は b1 の部分集合 b3 ⊆ b1
b3 は b1 の真部分集合 b3 ⊂ b1
b3 は b5 の部分集合 b3 ⊆ b5
b3 は b5 の真部分集合ではない。
b4 は b1 の部分集合 b4 ⊆ b1
b4 は b1 の真部分集合 b4 ⊂ b1
※ 図では b4 が b1 の外にありますが、空集合は全ての集合の真部分集合です。
新版明解C++中級編 p.84 演習2-7
前回《その131》のビットベクトルによる集合クラス BitSet に対して、以下の関数を追加せよ。
・集合の最小要素の値(空集合であれば -1)を返す関数 min
int min() const;
・集合の最大要素の値(空集合であれば -1)を返す関数 max
int max() const;
・集合の全要素を削除して空集合にする関数 clear
void clear();
・集合を集合 r と交換する(全要素を交換する)関数 swap
void swap(BitSet& r);
・集合 s1 と s2 を交換する非メンバ関数 swap
void swap(BitSet& s1, BitSet& s2);
・集合 s1 と s2 の対称差を求めて返却する関数 symmetric_difference
※ 集合 A, B に対する対称差(symmetric difference)とは、A - B ∪ B - A のことである。
BitSet symmetric_difference(const BitSet& s1, const BitSet& s2);
・集合 s1 と s2 の積集合を求めて返却する関数 &
BitSet operator&(const BitSet& s1, const BitSet& s2);
・集合 s1 と s2 の和集合を求めて返却する関数 |
BitSet operator|(const BitSet& s1, const BitSet& s2);
・集合 s1 と s2 の差集合を求めて返却する関数 -
BitSet operator-(const BitSet& s1, const BitSet& s2);
・集合が s の部分集合であるかどうかを判定する関数 is_subset_of
bool is_subset_of(const BitSet& s);
・集合が s の真部分集合であるかどうかを判定する関数 is_proper_subset_of
bool is_proper_subset_of(const BitSet& s);
// BitSet.h
#ifndef ___Class_BitSet
#define ___Class_BitSet
#include <limits>
#include <string>
#include <iostream>
class BitSet {
static const int LONG_BIT
= std::numeric_limits<unsigned long>::digits;
unsigned long bits;
static bool is_valid(int v) {
return v >= 0 && v < LONG_BIT;
}
static unsigned long set_of(int e) {
return 1UL << e;
}
public:
static int max_element() { return LONG_BIT - 1; }
static int min_element() { return 0; }
BitSet() : bits(0UL) { }
BitSet(const int e[], int n) : bits(0UL) {
for (int i = 0; i < n; i++)
add(e[i]);
}
bool contains(int e) const;
void add(int e);
void remove(int e);
bool empty() const;
int size() const;
BitSet& operator&=(const BitSet& r);
BitSet& operator|=(const BitSet& r);
BitSet& operator-=(const BitSet& r);
bool operator==(const BitSet& r) const;
bool operator!=(const BitSet& r) const;
// 演習2-7 で追加(メンバ関数) ---↓
int min() const;
int max() const;
void clear();
void swap(BitSet& r);
bool is_subset_of(const BitSet& s);
bool is_proper_subset_of(const BitSet& s);
// ------------------------------↑
std::string to_string() const;
std::string bit_string() const;
};
// 演習2-7 で追加(非メンバ関数) -----↓
void swap(BitSet& s1, BitSet& s2);
BitSet symmetric_difference(const BitSet& s1, const BitSet& s2);
BitSet operator&(const BitSet& s1, const BitSet& s2);
BitSet operator|(const BitSet& s1, const BitSet& s2);
BitSet operator-(const BitSet& s1, const BitSet& s2);
// ----------------------------------↑
std::ostream& operator<<(std::ostream& os, const BitSet& x);
#endif
// BitSet.cpp
#include <sstream>
#include <iostream>
#include "BitSet.h"
using namespace std;
bool BitSet::contains(int e) const {
return is_valid(e) && (bits & set_of(e));
}
void BitSet::add(int e) {
if (is_valid(e))
bits |= set_of(e);
}
void BitSet::remove(int e) {
if (is_valid(e))
bits &= ~set_of(e);
}
bool BitSet::empty() const {
return !bits;
}
int BitSet::size() const {
int count = 0;
unsigned long x = bits;
while (x) { x &= x - 1; count++; }
return count;
}
BitSet& BitSet::operator&=(const BitSet& r) {
bits &= r.bits;
return *this;
}
BitSet& BitSet::operator|=(const BitSet& r) {
bits |= r.bits;
return *this;
}
BitSet& BitSet::operator-=(const BitSet& r) {
bits &= ~r.bits;
return *this;
}
bool BitSet::operator==(const BitSet& r) const {
return bits == r.bits;
}
bool BitSet::operator!=(const BitSet& r) const {
return bits != r.bits;
}
// 演習2-7 で追加(メンバ関数) -----↓
// 最小要素の値
int BitSet::min() const {
int n = -1; // 空集合のときは -1 を返す。
for (int i = 0; i < LONG_BIT; i++) {
if (bits & set_of(i)) { n = i; break; }
}
return n;
}
// 最大要素の値
int BitSet::max() const {
int n = -1; // 空集合のときは -1 を返す。
for (int i = LONG_BIT - 1; i >= 0; i--) {
if (bits & set_of(i)) { n = i; break; }
}
return n;
}
// 空集合にする。
void BitSet::clear() { *this = BitSet(); }
// 集合 r と交換
void BitSet::swap(BitSet& r) { BitSet temp = r; r = *this; *this = temp; }
// 集合 s の部分集合か。
bool BitSet::is_subset_of(const BitSet& s) {
BitSet temp = *this;
return (temp -= s).empty() ? true : false;
}
// 集合 s の真部分集合か。
bool BitSet::is_proper_subset_of(const BitSet& s) {
BitSet temp1 = *this; BitSet temp2 = s;
return ((temp1 -= s).empty() && temp2 != *this) ?
true : false;
}
// --------------------------------↑
string BitSet::to_string() const {
ostringstream s;
int set[LONG_BIT];
int count = 0;
for (int i = 0; i < LONG_BIT; i++)
if (bits & set_of(i)) set[count++] = i;
s << "{";
if (count) {
for (int i = 0; i < count - 1; i++)
s << set[i] << ", ";
s << set[count - 1];
}
s << "}";
return s.str();
}
string BitSet::bit_string() const {
char bp[LONG_BIT + 1];
for (int i = LONG_BIT - 1; i >= 0; i--)
bp[LONG_BIT - i - 1] = (set_of(i) & bits) ? '1' : '0';
bp[LONG_BIT] = '\0';
return string(bp);
}
// 演習2-7 で追加(非メンバ関数) ---↓
// 集合 s1 と s2 を交換
void swap(BitSet& s1, BitSet& s2) {
BitSet temp = s1; s1 = s2; s2 = temp;
}
// 集合 s1 と s2 の対称差
BitSet symmetric_difference(const BitSet& s1, const BitSet& s2) {
BitSet temp1 = s1; BitSet temp2 = s2;
temp1 -= s2; temp2 -= s1;
return temp1 |= temp2;
}
// 集合 s1 と s2 の積集合
BitSet operator&(const BitSet& s1, const BitSet& s2) {
BitSet temp = s1;
return temp &= s2;
}
// 集合 s1 と s2 の和集合
BitSet operator|(const BitSet& s1, const BitSet& s2) {
BitSet temp = s1;
return temp |= s2;
}
// 集合 s1 と s2 の差集合( s1 - s2 )
BitSet operator-(const BitSet& s1, const BitSet& s2) {
BitSet temp = s1;
return temp -= s2;
}
// --------------------------------↑
ostream& operator<<(ostream& os, const BitSet& x) {
return os << x.to_string();
}
// BitSetTest.cpp
#include <iostream>
#include "BitSet.h"
using namespace std;
int main() {
int a1[] = { 0, 1, 2, 3, 4, 5, 8 };
int a2[] = { 4, 5, 6, 7 };
int a3[] = { 0, 8 };
BitSet b1(a1, sizeof(a1) / sizeof(a1[0]));
BitSet b2(a2, sizeof(a2) / sizeof(a2[0]));
BitSet b3(a3, sizeof(a3) / sizeof(a3[0]));
BitSet b4;
BitSet b5 = b3;
cout << "b1 = "; cout << b1 << '\n';
cout << "b2 = "; cout << b2 << '\n';
cout << "b3 = "; cout << b3 << '\n';
cout << "b4 = "; cout << b4 << '\n';
cout << '\n';
cout << "b1.min(); … " << b1.min() << '\n';
cout << "b1.max(); … " << b1.max() << '\n';
cout << "b4.min(); … " << b4.min() << '\n';
cout << "b4.max(); … " << b4.max() << "\n\n";
BitSet temp = b1;
cout << "temp = "; cout << temp << '\n';
cout << "◆temp.clear();" << '\n';
temp.clear();
cout << "temp = "; cout << temp << '\n';
cout << '\n';
cout << "◆b1.swap(b2);" << '\n';
b1.swap(b2);
cout << "b1 = "; cout << b1 << '\n';
cout << "b2 = "; cout << b2 << '\n';
cout << "◆swap(b1, b2);" << '\n';
swap(b1, b2);
cout << "b1 = "; cout << b1 << '\n';
cout << "b2 = "; cout << b2 << '\n';
cout << '\n';
cout << "◆symmetric_difference(b1, b2); // 対称差" << '\n';
cout << symmetric_difference(b1, b2) << '\n';
cout << '\n';
cout << "◆b1 & b2 // 積集合" << '\n';
cout << (b1 & b2) << '\n';
cout << "◆b1 | b2 // 和集合" << '\n';
cout << (b1 | b2) << '\n';
cout << "◆b1 - b2 // 差集合" << '\n';
cout << (b1 - b2) << '\n';
cout << '\n';
cout << "◆b1.is_subset_of(b3); // 部分集合であるかどうか" << '\n';
cout << boolalpha << b1.is_subset_of(b3) << '\n';
cout << "◆b3.is_subset_of(b1);" << '\n';
cout << boolalpha << b3.is_subset_of(b1) << '\n';
cout << "◆b1.is_subset_of(b4);" << '\n';
cout << boolalpha << b1.is_subset_of(b4) << '\n';
cout << "◆b4.is_subset_of(b1);" << '\n';
cout << boolalpha << b4.is_subset_of(b1) << '\n';
cout << "◆b3.is_subset_of(b5);" << '\n';
cout << boolalpha << b3.is_subset_of(b5) << '\n';
cout << "◆b5.is_subset_of(b3);" << '\n';
cout << boolalpha << b5.is_subset_of(b3) << "\n\n";
cout << "◆b1.is_proper_subset_of(b3); // 真部分集合であるかどうか" << '\n';
cout << boolalpha << b1.is_proper_subset_of(b3) << '\n';
cout << "◆b3.is_proper_subset_of(b1);" << '\n';
cout << boolalpha << b3.is_proper_subset_of(b1) << '\n';
cout << "◆b1.is_proper_subset_of(b4);" << '\n';
cout << boolalpha << b1.is_proper_subset_of(b4) << '\n';
cout << "◆b4.is_proper_subset_of(b1);" << '\n';
cout << boolalpha << b4.is_proper_subset_of(b1) << '\n';
cout << "◆b3.is_proper_subset_of(b5);" << '\n';
cout << boolalpha << b3.is_proper_subset_of(b5) << '\n';
cout << "◆b5.is_proper_subset_of(b3);" << '\n';
cout << boolalpha << b5.is_proper_subset_of(b3) << "\n\n";
cout << "◆(((b1 - b3 | b2) | b3) & b3)" << '\n';
cout << (((b1 - b3 | b2) | b3) & b3) << '\n';
}
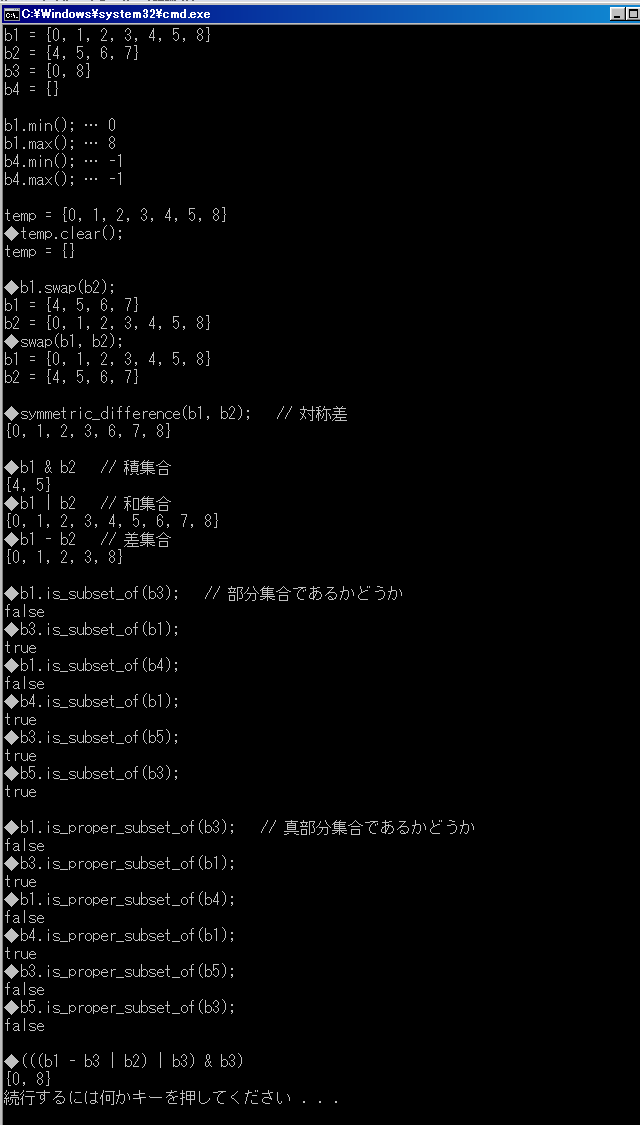
出力結果と見比べるのに使えるので、最初の図をもう一度ここに載せておきます。

この記事へのコメント
コメントを書く
この記事へのトラックバックURL
https://fanblogs.jp/tb/6976449
※ブログオーナーが承認したトラックバックのみ表示されます。
この記事へのトラックバック



