C++，C++/CX に挑戦！

◆ 新版明解C++入門編，新版明解C++中級編での学習。自分なりに要点を整理し、全演習問題を解いて、とりあえず一段落です。
◆ 続いて C# に移行予定でしたが、ここでは、このまま C++、そして C++/CX（UWP）についての記事をアップしていくことにします。
◆ C# については別のブログで初歩の初歩から学習を進めたいと思います。準備ができたらリンクを貼りますので、よろしくお願いします。

2017年11月12日

《その121》２のべき乗倍と左右へのビットシフト　&　p.55演習2-1

　２のべき乗倍と左右へのビットシフト


     0   00000000
     1   00000001
     2   00000010
     3   00000011
     4   00000100
     5   00000101
     6   00000110
     7   00000111
     8   00001000
     9   00001001 ◆
    10   00001010
    11   00001011
    12   00001100
    13   00001101
    14   00001110 
    15   00001111
    16   00010000
    17   00010001
    18   00010010 ◆
    19   00010011
    20   00010100
    21   00010101
    22   00010110
    23   00010111
    24   00011000
    25   00011001
    26   00011010
    27   00011011
    28   00011100
    29   00011101
    30   00011110
    31   00011111
    32   00100000

00001001 を 10進数で表すと、


       2の3乗×1 ＋ 2の2乗×0 ＋ 2の1乗×0 ＋ 2の0乗 ×1
    ＝    8  ×1 ＋    4  ×0 ＋    2  ×0 ＋    1   ×1
    ＝ 9

です。


9 ×2 ＝ 18

9 ×2 ＝ ( 2の3乗×1 ＋ 2の2乗×0 ＋ 2の1乗×0 ＋ 2の0乗 ×1 ) ×2
      ＝   2の4乗×1 ＋ 2の3乗×0 ＋ 2の2乗×0 ＋ 2の1乗 ×1
      ＝   2の4乗×1 ＋ 2の3乗×0 ＋ 2の2乗×0 ＋ 2の1乗 ×1＋ 2の0乗 ×0

となるので、10進数の 18 は 2進数で表すと 00010010 になります。

この計算からも、2進数で表した数は、2倍すると各ビットが左に 1 桁シフトすることがわかります。

新版明解C++中級編　p.55 演習2-1
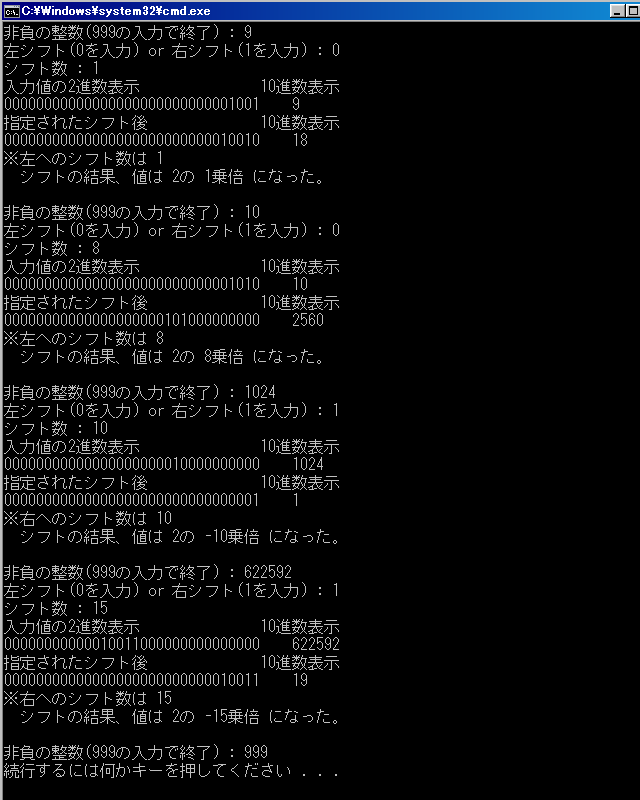
　符号無し整数を左右にシフトした値が、（オーバーフローしない限り）２のべき乗での乗算や除算の演算結果と一致することを確認するプログラムを作成せよ。


// p55_演習2-1
#include <iostream>
using namespace std;

int count_bits(unsigned x) {
    int bits = 0;
    while (x) {
        if (x & 1U) bits++;
        x >>= 1;
    }
    return bits;
}

int int_bits() {
    return count_bits(~0U);
}

void print_bits(unsigned x) {
    for (int i = int_bits() - 1; i >= 0; i--)
        cout << ((x >> i) & 1U ? '1' : '0');
}

int p(int a, int b) {    // 2の何乗倍であるかを返却する関数
    int n = 0;
    if (a < b)
        while (a != b) { n++; b /= 2; }
    else
        while (a != b) { n--; a /= 2; }
    return n;
}

int main() {
    unsigned u0, u1;
    int l_r, shift;

    while (1) {
        cout << "非負の整数(999の入力で終了) : "; cin >> u0;
        if (u0 == 999) break;
        u1 = u0;

        cout << "左シフト(0を入力) or 右シフト(1を入力) : ";
        cin >> l_r;
        cout << "シフト数 : "; cin >> shift;

        for (int i = 0; i < shift; i++) {
            if (l_r) { u1 >>= 1; }
            else     { u1 <<= 1; }
        }

        cout << "入力値の2進数表示               10進数表示\n";
        print_bits(u0);
        cout << "    " << u0 << '\n';

        cout << "指定されたシフト後　　　    　　10進数表示\n";
        print_bits(u1);
        cout << "    " << u1 << '\n';

        if (l_r) cout << "※右";
        else     cout << "※左";
        cout << "へのシフト数は " << shift << '\n';
        cout << "　シフトの結果、値は 2の " << p(u0, u1)
             << "乗倍 になった。\n\n";
    }
}