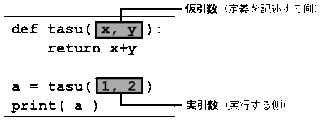
2020年12月20日
Pythonで扱う数値
記事内容の出典:フリーテキスト「Python3入門」
このページの更新:2020/12/25
基本的な計算
Pythonでは加減乗除をはじめとする数値の計算ができます.基本的な演算子を下に示します.
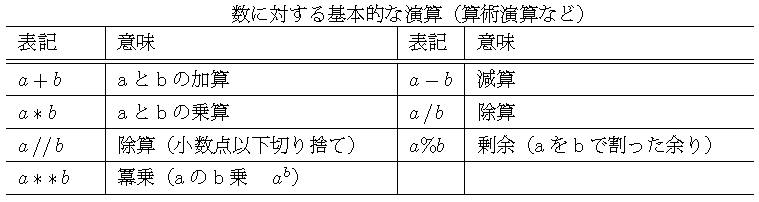
(表の出典:フリーテキスト「Python3入門」)
整数(int型)
整数とは小数点以下の部分を持たない数値です.Pythonでは大きな値の整数が扱えます.次の例は2の1000乗を計算するものです.
2**1000
実行結果:
10715086071862673209484250490600018105614048117055336074437503883703510511249361
22493198378815695858127594672917553146825187145285692314043598457757469857480393
45677748242309854210746050623711418779541821530464749835819412673987675591655439
46077062914571196477686542167660429831652624386837205668069376
浮動小数点数(float型)
小数点以下の部分を持つ数値は浮動小数点数(float型)の値として扱われます.この型の値として扱える桁数は約16桁程度です.例えば,先と同じような計算を float 型で実行すると次のようになります.
2.0**1000.0
実行結果:
1.0715086071862673e+301
この表示は指数表現と呼ばれる形式で,上の結果は「1.0715086071862673*(10**301)」と解釈することができます.指数表現は入力段階で用いることもできます.(次の例)
0.3141592653589793e1
実行結果:
3.141592653589793
float型で扱える最大値と最小値
float型は扱える値の範囲(絶対値の範囲)に制限があり,安全な形で計算処理を行うにはそれらを意識したほうが良いです.float型の絶対値の最大値と最小値を調べるには sys モジュールを使用します.
具体的な手順としては,まず sys モジュールを import して使用します.そして最大値は sys.float_info.max,最小値(絶対値)は sys.float_info.min を参照します.(次の例)
import sys
print( sys.float_info.max )
print( sys.float_info.min )
実行結果:
1.7976931348623157e+308
2.2250738585072014e-308
float型の(絶対値)の最大値と最小値が得られています.float型の数値計算は,絶対値がこの範囲におさまる形で実行するように工夫する必要があります.
■ float型の計算における誤差
float型の数値は限られた精度で表現されており,計算結果には誤差が含まれることがあります.計算誤差が目につくケースを1つ示します.
0.1 + 0.2
実行結果:
0.30000000000000004
このような単純な数値計算でも誤差が出ています.コンピュータ内部では数値は2進数の形で表現されており,特に小数点以下の部分の表現が10進数表現の場合と比べて異なります.つまり,10進数の表現で小数点以下の桁の長さが有限であっても,それを2進数で表現しようとすると循環小数となってしまうことがしばしばあります.逆に,2進数表現において小数点以下の桁の長さが有限である場合には計算結果に誤差が出ません.(次の例)
0.5 + 0.25
実行結果:
0.75
■ 桁の丸め
round 関数を使うと小数点以下の桁数を指定した長さに丸めることができます.round 関数は
round( 値, 小数点以下の長さ )
として使います.(次の例)
a = 1.0 / 3.0
print( a )
print( round(a,2) )
実行結果:
0.3333333333333333
0.33
複素数(complex型)
Pythonでは複素数が扱えます.虚数単位は j で表記します.次の例は 2+3j と 2-3j の積を求めるものです.
c1 = 2+3j
c2 = 2-3j
print( c1*c2 )
実行結果:
(13+0j)
このように,虚部が 0 となっても 0j という形で残ります.
複素数の実部と虚部は,「.real」「.imag」という接尾辞をつけることで参照することができます.(次の例)
print( c1.real )
print( c1.imag )
実行結果:
2.0
3.0
注意)「.real」「.imag」という接尾辞をつけたものにイコール「=」で値を与えることはできません.
complexのコンストラクタ「complex( 実部, 虚部 )」を使用すると,実部と虚部を明に与える形で複素数を作成することができます.
n1 = 5
n2 = 7
complex( n1, n2 )
実行結果:
(5+7j)
数学関数
mathモジュールを読み込むと各種の数学関数が使用できます.例えば円周率(π)は math.pi,正接関数(タンジェント)は math.tan(x) などとします.(次の例)
import math
p = math.pi
print( p )
print( math.tan(p/3) )
実行結果:
3.141592653589793
1.7320508075688767
mathモジュールが提供する関数の一部を下に示します.

(表の出典:フリーテキスト「Python3入門」)
「math.」の後ろに上の表の関数や定数を記述して使います.
参考)複素数の関数は cmath モジュールが提供します.
最大値,最小値,絶対値
関数 max,min,abs でそれぞれ最大値,最小値,絶対値を求めることができます.
max( 値1, 値2, … ,値n ) → 値1, 値2, … ,値n の中の最大の値を返す
min( 値1, 値2, … ,値n ) → 値1, 値2, … ,値n の中の最小の値を返す
abs( 値 ) → 値 の絶対値を返す
プログラム例:
print( max(1,2,3,4,3,2) )
print( min(1,2,3,4,3,2) )
print( abs(-5) )
実行結果:
4
1
5
関数 abs に複素数を与えると,そのノルム(実部と虚部の2乗和の平方根)を算出します.
abs(3+4j)
実行結果:
5.0
関数 min,max には,値のリストを与えることもできます.
lst = [1,2,3,4,3,2]
print( max(lst) )
print( min(lst) )
実行結果:
4
1
リストは複数の値を書き並べるデータ構造で,詳しくは別の記事で解説します.
高精度計算(桁の長い浮動小数点数の扱い)
Python本来の浮動小数点数(float型)では表現できる数値の桁が限られており,その限界を超えた精度の計算(長い桁の計算)ができません.しかし,mpmath.org(https://mpmath.org/)が開発した mpmath というライブラリを使用するとそれが可能になります.このライブラリは Google Colab. にはインストールされており,Pythonプログラム側でインポートすることで使用できます.
mpmath ライブラリを使用するには
1) mpmath から必要な部分を読み込む(インポート)
2) 計算できる精度(桁の長さ)を設定する
という作業をします.(次の例)
from mpmath import mp
mp.dps = 50
1行目がライブラリのインポートで,2行目が桁数の設定です.この例では表現できる桁数を50桁に設定しています.
mpmathライブラリの利用において意識しなければならないことがあります.それは,値の型が float ではなく mpf や mpc といった独特のデータ型であるという点です.従って,長い桁の浮動小数点数を入力する際に少し特殊な作業を行います.(次の例)
a = mp.mpf('1.0')
print( a )
実行結果:
1.0
これは,変数 a に数値 1.0 を与える例ですが,数値の表現として1行目にあるように
mp.mpf('数値の表現')
と記述しなければなりません.またこの例ではprintで値を表示して確認していますが,変数 a の値を直接照会すると mpf オブジェクトの形式であることがわかります.(次の例)
a
実行結果:
mpf('1.0')
では次に,この a の値を 3 で割ってみましょう.(次の例)
print( a / 3.0 )
実行結果:
0.33333333333333333333333333333333333333333333333333
計算結果が長い桁で得られていることがわかります.
mpmath は math ライブラリと似た使い方ができ,「mp.」という接頭辞を付けて定数や関数を使うことができます.先に math ライブラリのところで示した例と同様の処理をやってみましょう.(次の例)
p = mp.pi
print( p )
print( mp.tan(p/3) )
実行結果:
3.1415926535897932384626433832795028841971693993751
1.7320508075688772935274463415058723669428052538104
円周率,タンジェントの値が長い桁で得られています.
■ mpmath の複素数:mpc オブジェクト
mpmath で複素数の値を入力するには
mp.mpc('値の表現')
とします.例えば,複素数の形式で -2.0 を入力するには次のようにします.
c = mp.mpc('-2.0')
print( c )
実行結果:
(-2.0 + 0.0j)
変数 c に (-2.0 + 0.0j) が得られています.この値もPython本来のcomplex型とは異なります.(次の例)
c
実行結果:
mpc(real='-2.0', imag='0.0')
mpc オブジェクトとしての値であることがわかります.更に,この値の平方根を求めてみましょう.
print( mp.sqrt(c) )
実行結果:
(0.0 + 1.4142135623730950488016887242096980785696718753769j)
結果が複素数として(mpcオブジェクトとして)得られています.
分数の扱い
fractionsモジュールを利用すると分数(有理数)を扱うことができます.分数計算のための機能を読み込むには
from fractions import Fraction
とします.この末尾にある Fraction というのが分数を表現するためのもので,分数の値を作成するには
Fraction( 分子, 分母 )
と記述します.この記述でできた分数(Fractionオブジェクト)を print で表示すると 分子/分母 の形式で表示されます.(次の例)
a = Fraction(2,3)
b = Fraction(3,4)
print( a )
print( b )
実行結果:
2/3
3/4
Fraction オブジェクトは float や int といった普通の数値と一緒に計算式の中に記述することができます.(次の例)
c = a + b + 1
print( c )
実行結果:
29/12
計算する際の約分や通分は自動的に行われます.
分数を表す浮動小数点数の近似値を求めるには float( 分数 ) と記述します.(次の例)
float( c )
実行結果:
2.4166666666666665
分数以外の値を分数に変換するには Fraction( 元の値 ) と記述します.(次の例)
q = Fraction( 1.23 )
print( d )
実行結果:
2769713770832855/2251799813685248
1.23 を分数に変換するとこのように分母・分子ともの大きな値となってしまいました.これは,float の値がコンピュータ内部では2進数で表現されており,1.23 という値が2進数では循環小数になってしまうという事情によるものです.このような場合,分母の大きさを制限して「近似値としての分数」に変換すると自然な形になることがあります.次の例のように,分数に対して limit_denominator メソッドを実行すると近似値の分数が得られます.
print( q.limit_denominator(100) )
実行結果:
123/100
limit_denominator の引数に変換後の分数の上限を与えます.
 Python3 の基礎 − 超入門・再入門 −
Python3 の基礎 − 超入門・再入門 −【このカテゴリーの最新記事】
この記事へのコメント
コメントを書く
この記事へのトラックバックURL
https://fanblogs.jp/tb/10421181
※ブログオーナーが承認したトラックバックのみ表示されます。
この記事へのトラックバック