画像
　このベクトルも長さは 1 です。
　実数で扱っていた絶対値記号をそのまま借用して、

画像
と書くことにします。数直線上の絶対値記号は、数の正負を問わずに原点からの距離を表していましたけれど、その考え方はそのまま平面上でも適用されているわけです。向きを少しずつ変えれば、大きさ 1 のベクトルはいくらでも作り出すことができます。

　

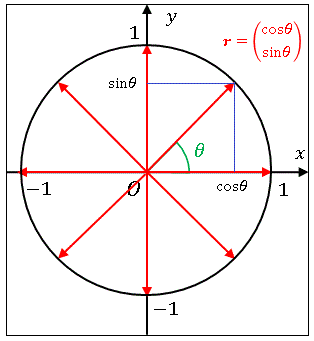
　つまり数直線上の +1 と −1 に相当する数が平面上では無数に存在することになるのです。ところで上の図にあるように、大きさ 1 のベクトルの先端は半径 1 の円を描くことがわかります。つまり半径 1 の円の方程式はベクトルを用いて

画像
と書くこともできます。ここまでくれば、前々回に少し触れた三角関数とのつながりが見えてきますね。半径 1 の円周上の点は x 軸から反時計回りに測った角度θを用いて (cosθ, sinθ) と表