れる概念です。

　数学では単位というものを使わずに、全ての量を自然数 1 と虚数単位 i で表したいのです（つまり自然数 1 と虚数単位 i だけが数学で使用される単位といえるかもしれません）。だから中学までに使用されてきた度数法というのは、現実世界で分度器を使って角度を測ったりするには便利ですけど、1°が自然数 1 とは異なる量だというのは、数学的にはちょっとまずいわけです（要するに美しくないのです）。

　さて、以上の説明を踏まえると、1 ラジアンとは自然数 1 に等しいはずです。
　そのために弧度法を導入したわけですからね。違っていたら大変です。
　つまり単位円の半径 1 と等しい長さです。これを円周との比率で考えてみると、半径 1 の円の周長は 2π ≒ 6.28 ですから、1 ラジアンは円周の 1/6 より少しだけ大きい値になっています。図にするとこんな感じです。

　

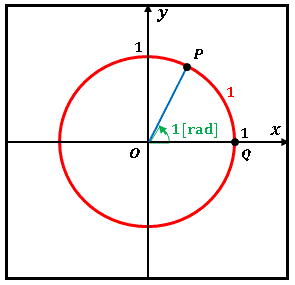
　線分 OQ と弧 PQ が等しく 1 になるようにとった角度が 1 ラジアンというわけです。1 ラジアンという言葉を聞いたときに、このイメージがぱっと頭に浮かぶようにしておいてくださいなー。数学は厳密な論証より先にイメージを掴んでおくことが大切ねー。それでは今回はこのへんでー。　≫ �A度数法と弧度法の変換