振動数列になるような漸化式
f(1) = 0, f(2) = 1, f(3) = 1 として3項間の漸化式
f(n + 3) = f(n + 2) - f(n)
によって定義される数列を考えます。具体的に書くと
f(4) = f(3) - f(1) = 1
f(5) = f(4) - f(2) = 0
f(6) = f(5) - f(3) = -1
・・・・・・・・・
のようになります。さて、この数列を横軸に n, 縦軸に f(n) をとって図示すると面白い形が現れます。
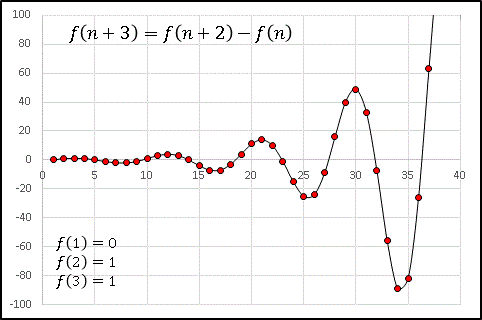
数列の各点を滑らかな線で結ぶと、f(n) は次第に振幅を増加させる振動関数のようになっているのです。漸化式の形が少しでも変わるとグラフの様子は一変します。今度は
f(n + 3) = f(n + 2) - f(n)/2
という数列を図示してみましょう。
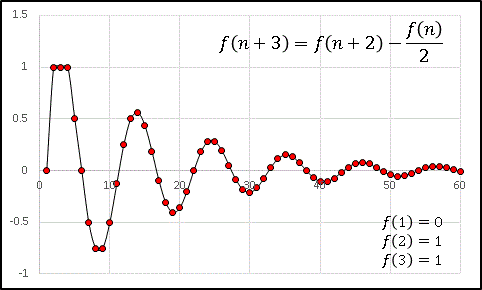
今度は振幅自体がとても小さくなったうえに、減衰振動関数となりました。さらに
f(n + 3) = f(n + 2)/2 + f(n + 1) - f(n)
で定