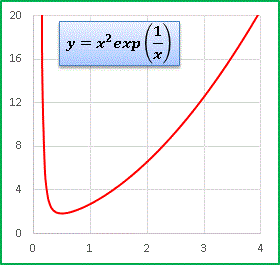
極小値までひと息に急減して、そのあとは増加に転じます。
　この関数を微分すると、

y′= (2x − 1)exp(1 / x)
x < 1 / 2 で y′ < 0
x > 1 / 2 で y′ > 0
となるので極小値は x = 0.5 です。連続関数ではありますが、この極値を境にして関数の様相は一変していますね。x が十分に大きいところでは exp(1 / x) ≒ 1 とみなせるので、 y ≒ x 2 となります。

　次は exp の変数を logx / x としてみます：



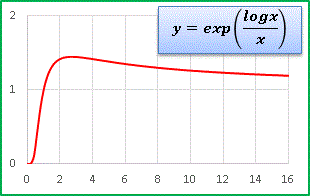
　かなり特徴のある関数です。グラフでは少し見えにくいですが [0, 0.3] あたりでは x 軸にべったりと張り付いています。そのあと比較的大きな勾配で値が増加していきますが、x が大きくなるとすぐに勾配を緩めながら緩やかな減少に転じます。
　
グラフの概形を非対称に変えます　e の肩に x の 2 次関数を乗せます：

y = exp(−ax2 + bx)　（a > 0, b は任意）
　まずは b = 0 として a を変化させてみます：