≫ [Amazon書籍] もういちど読む数研の高校化学

　以前に正葉曲線 r = sin(nθ) を扱いました。
　n = 1 から n = 4 のグラフの概形を再掲します。

　

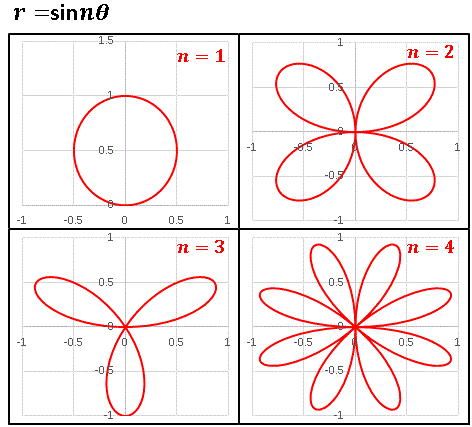
　今回はこの正葉曲線の中身にさらに三角関数を入れ子にして、色々なグラフを描いてみようと思います。

カレーパンとクリームパン　まず sin を入れ子にした

r = sin[θ+ sin(nθ)]
という極方程式のグラフを調べてみます。直交座標への変換は

x = sin[θ+ sin(nθ)] cosθ
y = sin[θ+ sin(nθ)] sinθ
となります。 n = 1 から n = 3 まで並べてみましょう。

　

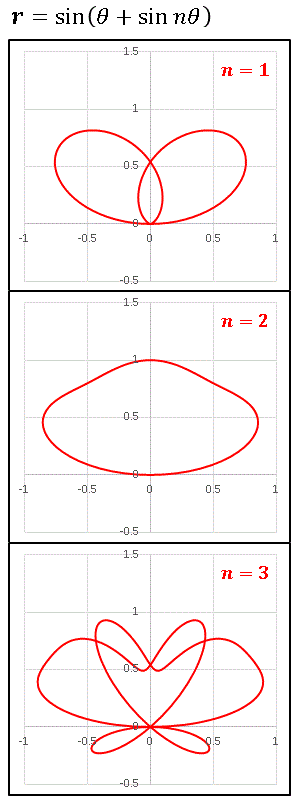
　個人的に気に入ったのは n = 2 のグラフです。
　何とも表